A Modular Conditional Diffusion Framework for Image Reconstruction

Diffusion Probabilistic Models (DPMs) have been recently utilized to deal with various blind image restoration (IR) tasks, where they have demonstrated outstanding performance in terms of perceptual quality. However, the task-specific nature of existing solutions and the excessive computational costs related to their training, make such models impractical and challenging to use for different IR tasks than those that were initially trained for. This hinders their wider adoption, especially by those who lack access to powerful computational resources and vast amount of training data. In this work we aim to address the above issues and enable the successful adoption of DPMs in practical IR-related applications. Towards this goal, we propose a modular diffusion probabilistic IR framework (DP-IR), which allows us to combine the performance benefits of existing pre-trained state-of-the-art IR networks and generative DPMs, while it requires only the additional training of a relatively small module (0.7M params) related to the particular IR task of interest. Moreover, the architecture of the proposed framework allows for a sampling strategy that leads to at least four times reduction of neural function evaluations without suffering any performance loss, while it can also be combined with existing acceleration techniques such as DDIM. We evaluate our model on four benchmarks for the tasks of burst JDD-SR, dynamic scene deblurring, and super-resolution. Our method outperforms existing approaches in terms of perceptual quality while it retains a competitive performance with respect to fidelity metrics.

Robust Two-View Geometry Estimation with Implicit Differentiation

We present a novel two-view geometry estimation framework which is based on a differentiable robust loss function fitting. We propose to treat the robust fundamental matrix estimation as an implicit layer, which allows us to avoid backpropagation through time and significantly improves the numerical stability. To take full advantage of the information from the feature matching stage we incorporate learnable weights that depend on the matching confidences. In this way our solution brings together feature extraction, matching and two-view geometry estimation in a unified end-to-end trainable pipeline. We evaluate our approach on the camera pose estimation task in both outdoor and indoor scenarios. The experiments on several datasets show that the proposed method outperforms both classic and learning-based state-of-the-art methods by a large margin. The project webpage is available at: https://github.com/VladPyatov/ihls

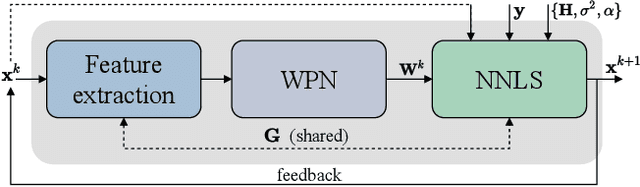
Iterative Reweighted Least Squares Networks With Convergence Guarantees for Solving Inverse Imaging Problems

In this work we present a novel optimization strategy for image reconstruction tasks under analysis-based image regularization, which promotes sparse and/or low-rank solutions in some learned transform domain. We parameterize such regularizers using potential functions that correspond to weighted extensions of the $\ell_p^p$-vector and $\mathcal{S}_p^p$ Schatten-matrix quasi-norms with $0 < p \le 1$. Our proposed minimization strategy extends the Iteratively Reweighted Least Squares (IRLS) method, typically used for synthesis-based $\ell_p$ and $\mathcal{S}_p$ norm and analysis-based $\ell_1$ and nuclear norm regularization. We prove that under mild conditions our minimization algorithm converges linearly to a stationary point, and we provide an upper bound for its convergence rate. Further, to select the parameters of the regularizers that deliver the best results for the problem at hand, we propose to learn them from training data by formulating the supervised learning process as a stochastic bilevel optimization problem. We show that thanks to the convergence guarantees of our proposed minimization strategy, such optimization can be successfully performed with a memory-efficient implicit back-propagation scheme. We implement our learned IRLS variants as recurrent networks and assess their performance on the challenging image reconstruction tasks of non-blind deblurring, super-resolution and demosaicking. The comparisons against other existing learned reconstruction approaches demonstrate that our overall method is very competitive and in many cases outperforms existing unrolled networks, whose number of parameters is orders of magnitude higher than in our case.

Learning Sparse and Low-Rank Priors for Image Recovery via Iterative Reweighted Least Squares Minimization

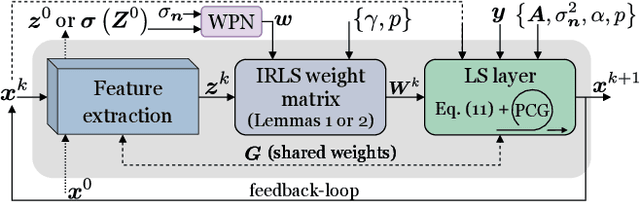
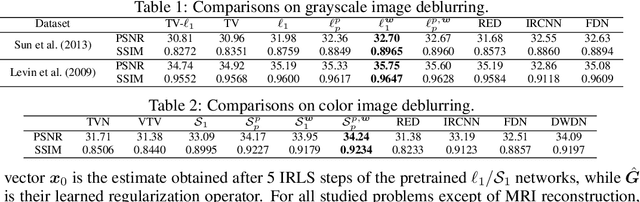
We introduce a novel optimization algorithm for image recovery under learned sparse and low-rank constraints, which we parameterize as weighted extensions of the $\ell_p^p$-vector and $\mathcal S_p^p$ Schatten-matrix quasi-norms for $0\!<p\!\le1$, respectively. Our proposed algorithm generalizes the Iteratively Reweighted Least Squares (IRLS) method, used for signal recovery under $\ell_1$ and nuclear-norm constrained minimization. Further, we interpret our overall minimization approach as a recurrent network that we then employ to deal with inverse low-level computer vision problems. Thanks to the convergence guarantees that our IRLS strategy offers, we are able to train the derived reconstruction networks using a memory-efficient implicit back-propagation scheme, which does not pose any restrictions on their effective depth. To assess our networks' performance, we compare them against other existing reconstruction methods on several inverse problems, namely image deblurring, super-resolution, demosaicking and sparse recovery. Our reconstruction results are shown to be very competitive and in many cases outperform those of existing unrolled networks, whose number of parameters is orders of magnitude higher than that of our learned models.

DeepRLS: A Recurrent Network Architecture with Least Squares Implicit Layers for Non-blind Image Deconvolution

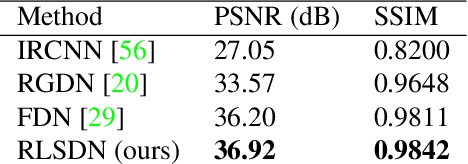
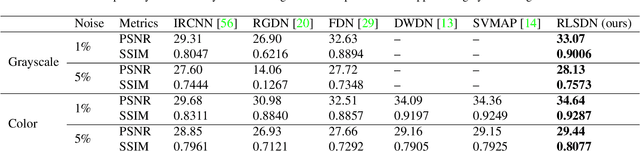
In this work, we study the problem of non-blind image deconvolution and propose a novel recurrent network architecture that leads to very competitive restoration results of high image quality. Motivated by the computational efficiency and robustness of existing large scale linear solvers, we manage to express the solution to this problem as the solution of a series of adaptive non-negative least-squares problems. This gives rise to our proposed Recurrent Least Squares Deconvolution Network (RLSDN) architecture, which consists of an implicit layer that imposes a linear constraint between its input and output. By design, our network manages to serve two important purposes simultaneously. The first is that it implicitly models an effective image prior that can adequately characterize the set of natural images, while the second is that it recovers the corresponding maximum a posteriori (MAP) estimate. Experiments on publicly available datasets, comparing recent state-of-the-art methods, show that our proposed RLSDN approach achieves the best reported performance both for grayscale and color images for all tested scenarios. Furthermore, we introduce a novel training strategy that can be adopted by any network architecture that involves the solution of linear systems as part of its pipeline. Our strategy eliminates completely the need to unroll the iterations required by the linear solver and, thus, it reduces significantly the memory footprint during training. Consequently, this enables the training of deeper network architectures which can further improve the reconstruction results.

NTIRE 2021 Challenge on Quality Enhancement of Compressed Video: Methods and Results

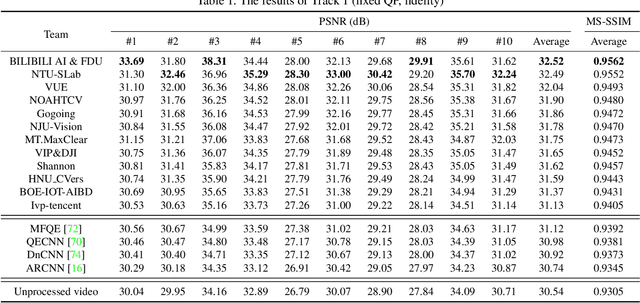
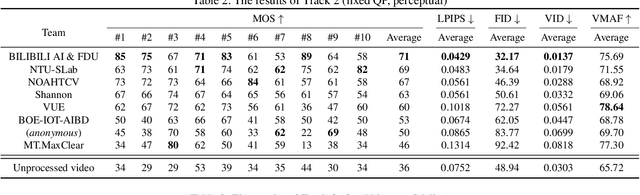
This paper reviews the first NTIRE challenge on quality enhancement of compressed video, with a focus on the proposed methods and results. In this challenge, the new Large-scale Diverse Video (LDV) dataset is employed. The challenge has three tracks. Tracks 1 and 2 aim at enhancing the videos compressed by HEVC at a fixed QP, while Track 3 is designed for enhancing the videos compressed by x265 at a fixed bit-rate. Besides, the quality enhancement of Tracks 1 and 3 targets at improving the fidelity (PSNR), and Track 2 targets at enhancing the perceptual quality. The three tracks totally attract 482 registrations. In the test phase, 12 teams, 8 teams and 11 teams submitted the final results of Tracks 1, 2 and 3, respectively. The proposed methods and solutions gauge the state-of-the-art of video quality enhancement. The homepage of the challenge: https://github.com/RenYang-home/NTIRE21_VEnh