Differentiable Rendering with Reparameterized Volume Sampling

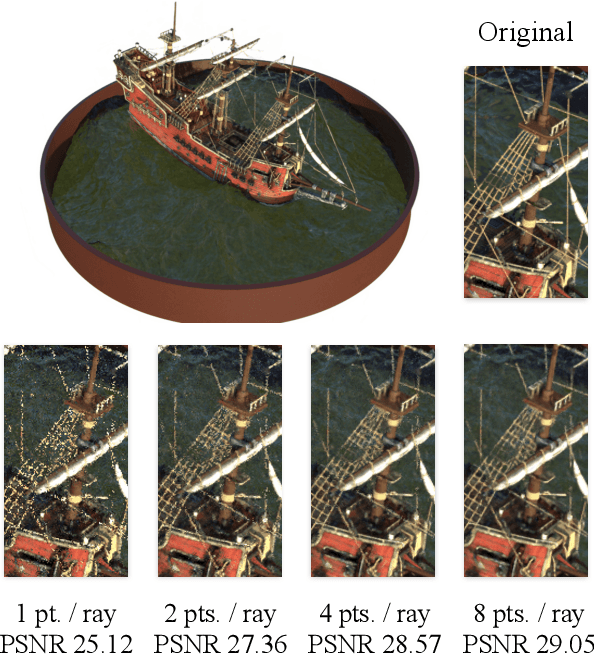
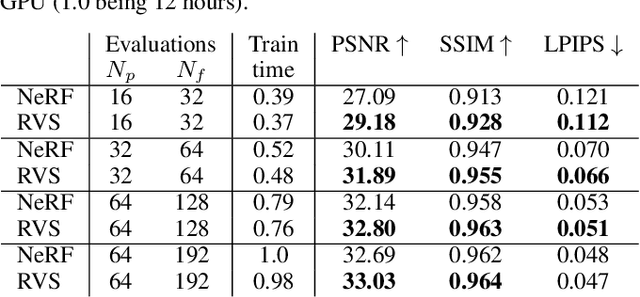
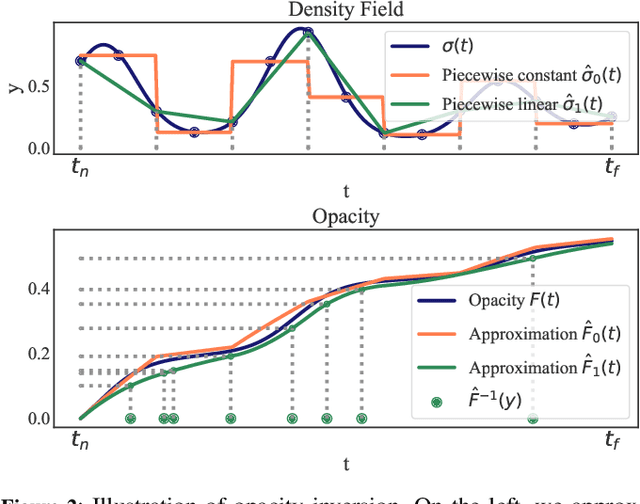
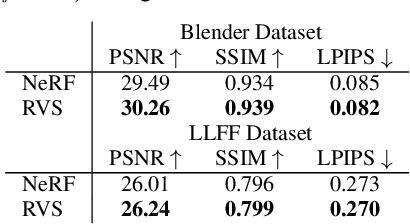
In view synthesis, a neural radiance field approximates underlying density and radiance fields based on a sparse set of scene pictures. To generate a pixel of a novel view, it marches a ray through the pixel and computes a weighted sum of radiance emitted from a dense set of ray points. This rendering algorithm is fully differentiable and facilitates gradient-based optimization of the fields. However, in practice, only a tiny opaque portion of the ray contributes most of the radiance to the sum. We propose an end-to-end differentiable sampling algorithm based on inverse transform sampling. It generates samples according to the probability distribution induced by the density field and picks non-transparent points on the ray. We utilize the algorithm in two ways. First, we propose a novel rendering approach based on Monte Carlo estimates. Such a rendering algorithm allows for optimizing a neural radiance field with just a few radiance field evaluations per ray. Second, we use the sampling algorithm to modify the hierarchical scheme used in the original work on neural radiance fields. In this setup, we were able to train the proposal network end-to-end without any auxiliary losses and improved the baseline performance.

Leveraging Recursive Gumbel-Max Trick for Approximate Inference in Combinatorial Spaces

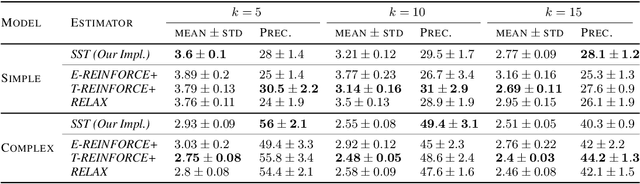
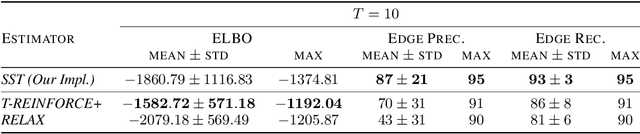
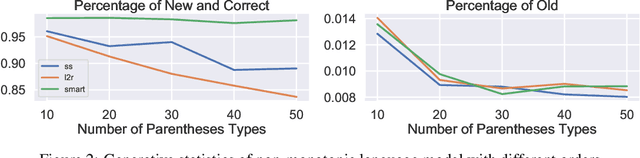
Structured latent variables allow incorporating meaningful prior knowledge into deep learning models. However, learning with such variables remains challenging because of their discrete nature. Nowadays, the standard learning approach is to define a latent variable as a perturbed algorithm output and to use a differentiable surrogate for training. In general, the surrogate puts additional constraints on the model and inevitably leads to biased gradients. To alleviate these shortcomings, we extend the Gumbel-Max trick to define distributions over structured domains. We avoid the differentiable surrogates by leveraging the score function estimators for optimization. In particular, we highlight a family of recursive algorithms with a common feature we call stochastic invariant. The feature allows us to construct reliable gradient estimates and control variates without additional constraints on the model. In our experiments, we consider various structured latent variable models and achieve results competitive with relaxation-based counterparts.

Low-variance Black-box Gradient Estimates for the Plackett-Luce Distribution

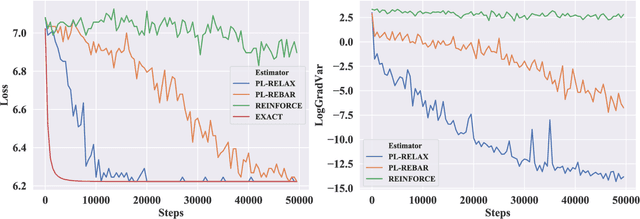
Learning models with discrete latent variables using stochastic gradient descent remains a challenge due to the high variance of gradient estimates. Modern variance reduction techniques mostly consider categorical distributions and have limited applicability when the number of possible outcomes becomes large. In this work, we consider models with latent permutations and propose control variates for the Plackett-Luce distribution. In particular, the control variates allow us to optimize black-box functions over permutations using stochastic gradient descent. To illustrate the approach, we consider a variety of causal structure learning tasks for continuous and discrete data. We show that our method outperforms competitive relaxation-based optimization methods and is also applicable to non-differentiable score functions.

Quantifying Learning Guarantees for Convex but Inconsistent Surrogates

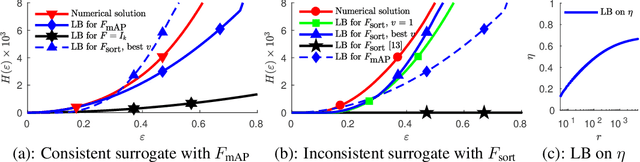
We study consistency properties of machine learning methods based on minimizing convex surrogates. We extend the recent framework of Osokin et al. (2017) for the quantitative analysis of consistency properties to the case of inconsistent surrogates. Our key technical contribution consists in a new lower bound on the calibration function for the quadratic surrogate, which is non-trivial (not always zero) for inconsistent cases. The new bound allows to quantify the level of inconsistency of the setting and shows how learning with inconsistent surrogates can have guarantees on sample complexity and optimization difficulty. We apply our theory to two concrete cases: multi-class classification with the tree-structured loss and ranking with the mean average precision loss. The results show the approximation-computation trade-offs caused by inconsistent surrogates and their potential benefits.

The Deep Weight Prior. Modeling a prior distribution for CNNs using generative models

Bayesian inference is known to provide a general framework for incorporating prior knowledge or specific properties into machine learning models via carefully choosing a prior distribution. In this work, we propose a new type of prior distributions for convolutional neural networks, deep weight prior, that in contrast to previously published techniques, favors empirically estimated structure of convolutional filters e.g., spatial correlations of weights. We define deep weight prior as an implicit distribution and propose a method for variational inference with such type of implicit priors. In experiments, we show that deep weight priors can improve the performance of Bayesian neural networks on several problems when training data is limited. Also, we found that initialization of weights of conventional networks with samples from deep weight prior leads to faster training.

Robust Variational Inference

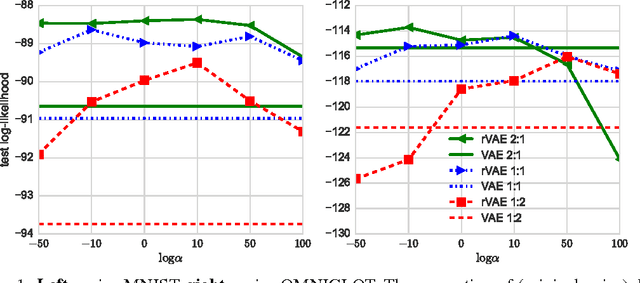
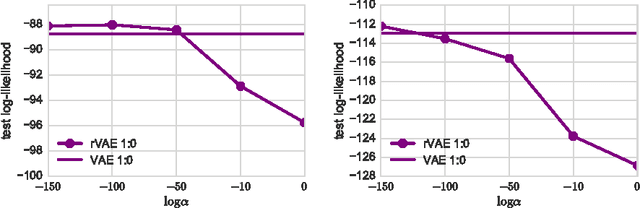
Variational inference is a powerful tool for approximate inference. However, it mainly focuses on the evidence lower bound as variational objective and the development of other measures for variational inference is a promising area of research. This paper proposes a robust modification of evidence and a lower bound for the evidence, which is applicable when the majority of the training set samples are random noise objects. We provide experiments for variational autoencoders to show advantage of the objective over the evidence lower bound on synthetic datasets obtained by adding uninformative noise objects to MNIST and OMNIGLOT. Additionally, for the original MNIST and OMNIGLOT datasets we observe a small improvement over the non-robust evidence lower bound.