Regularized Distribution Matching Distillation for One-step Unpaired Image-to-Image Translation

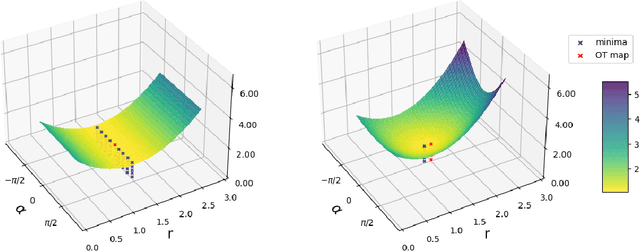
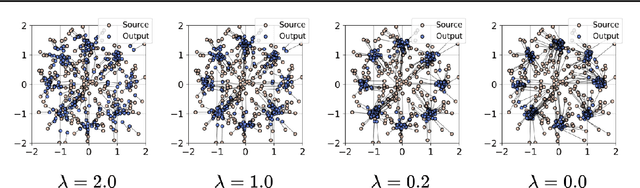
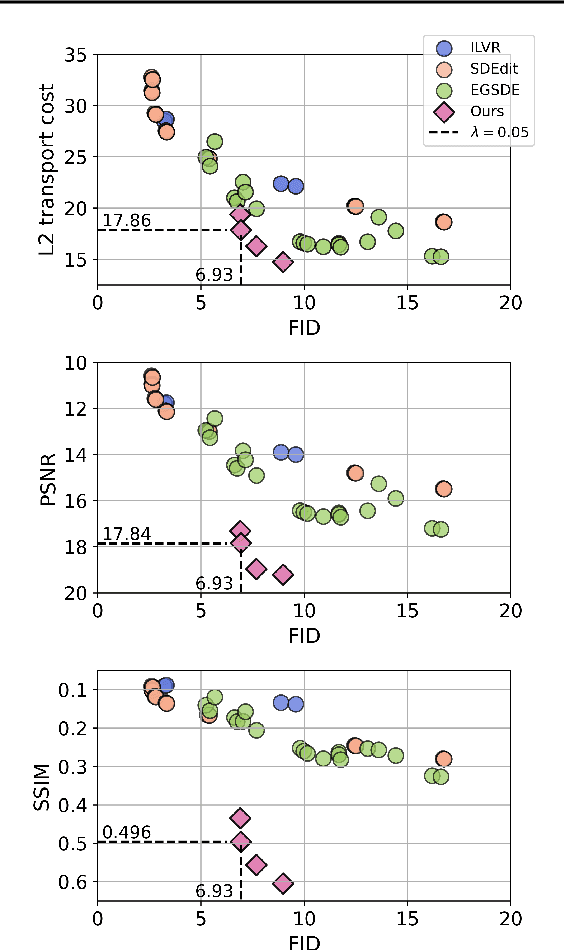
Diffusion distillation methods aim to compress the diffusion models into efficient one-step generators while trying to preserve quality. Among them, Distribution Matching Distillation (DMD) offers a suitable framework for training general-form one-step generators, applicable beyond unconditional generation. In this work, we introduce its modification, called Regularized Distribution Matching Distillation, applicable to unpaired image-to-image (I2I) problems. We demonstrate its empirical performance in application to several translation tasks, including 2D examples and I2I between different image datasets, where it performs on par or better than multi-step diffusion baselines.

Differentiable Rendering with Reparameterized Volume Sampling

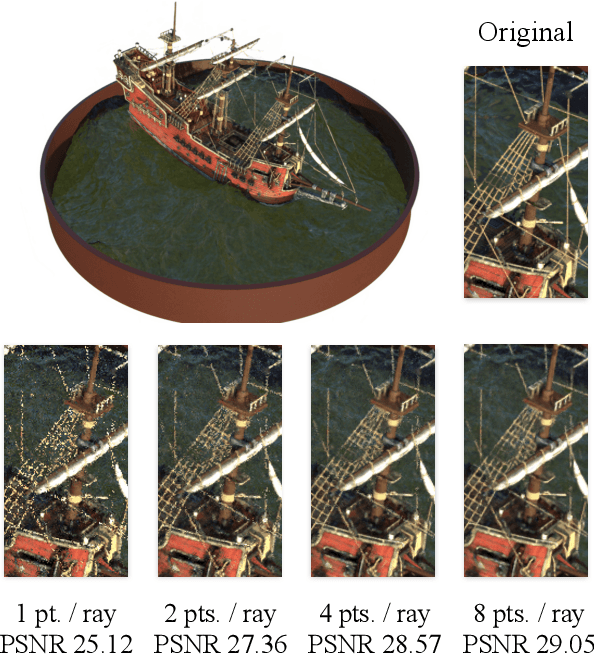
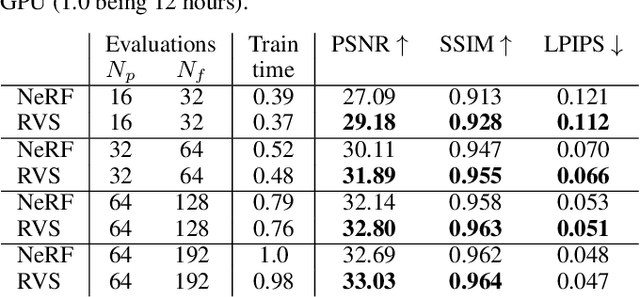
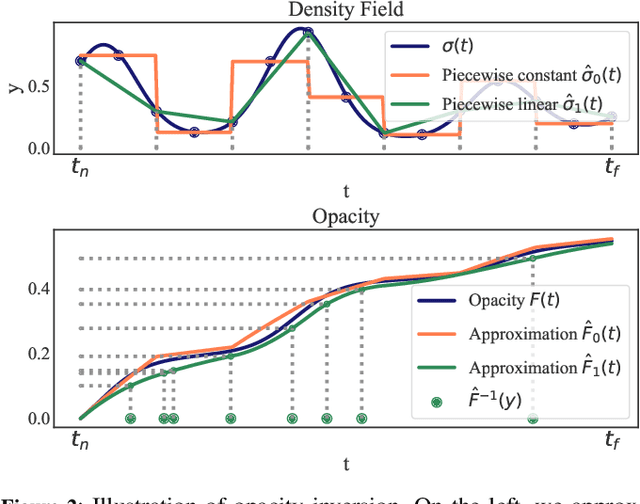
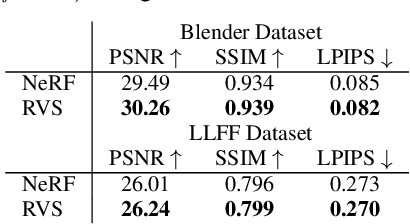
In view synthesis, a neural radiance field approximates underlying density and radiance fields based on a sparse set of scene pictures. To generate a pixel of a novel view, it marches a ray through the pixel and computes a weighted sum of radiance emitted from a dense set of ray points. This rendering algorithm is fully differentiable and facilitates gradient-based optimization of the fields. However, in practice, only a tiny opaque portion of the ray contributes most of the radiance to the sum. We propose an end-to-end differentiable sampling algorithm based on inverse transform sampling. It generates samples according to the probability distribution induced by the density field and picks non-transparent points on the ray. We utilize the algorithm in two ways. First, we propose a novel rendering approach based on Monte Carlo estimates. Such a rendering algorithm allows for optimizing a neural radiance field with just a few radiance field evaluations per ray. Second, we use the sampling algorithm to modify the hierarchical scheme used in the original work on neural radiance fields. In this setup, we were able to train the proposal network end-to-end without any auxiliary losses and improved the baseline performance.

Leveraging Recursive Gumbel-Max Trick for Approximate Inference in Combinatorial Spaces

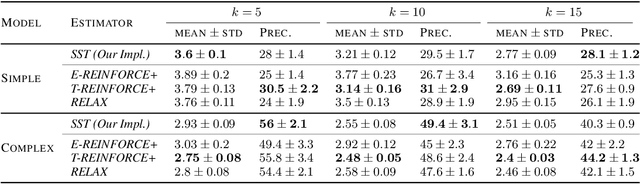
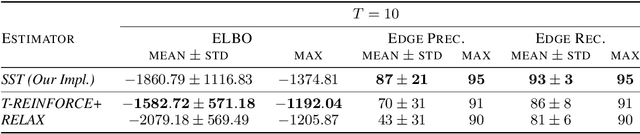
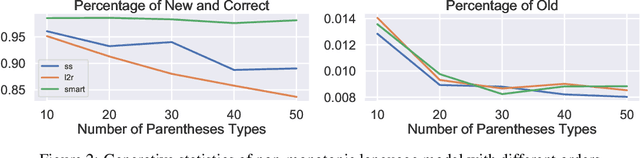
Structured latent variables allow incorporating meaningful prior knowledge into deep learning models. However, learning with such variables remains challenging because of their discrete nature. Nowadays, the standard learning approach is to define a latent variable as a perturbed algorithm output and to use a differentiable surrogate for training. In general, the surrogate puts additional constraints on the model and inevitably leads to biased gradients. To alleviate these shortcomings, we extend the Gumbel-Max trick to define distributions over structured domains. We avoid the differentiable surrogates by leveraging the score function estimators for optimization. In particular, we highlight a family of recursive algorithms with a common feature we call stochastic invariant. The feature allows us to construct reliable gradient estimates and control variates without additional constraints on the model. In our experiments, we consider various structured latent variable models and achieve results competitive with relaxation-based counterparts.