Monte Carlo Gradient Estimation in Machine Learning

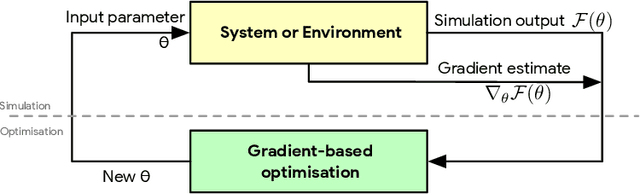
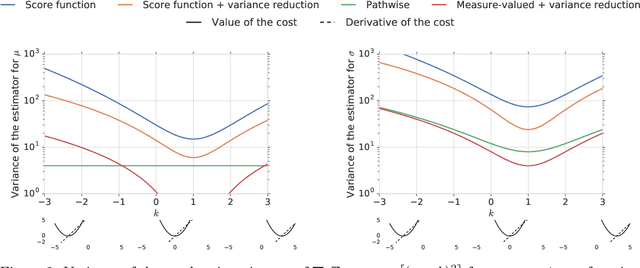
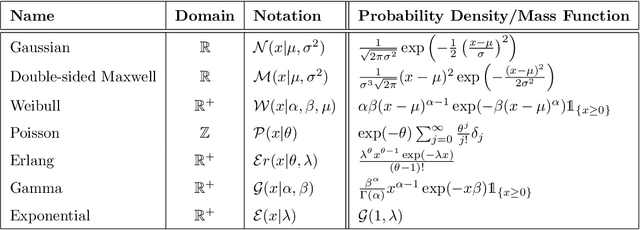
This paper is a broad and accessible survey of the methods we have at our disposal for Monte Carlo gradient estimation in machine learning and across the statistical sciences: the problem of computing the gradient of an expectation of a function with respect to parameters defining the distribution that is integrated; the problem of sensitivity analysis. In machine learning research, this gradient problem lies at the core of many learning problems, in supervised, unsupervised and reinforcement learning. We will generally seek to rewrite such gradients in a form that allows for Monte Carlo estimation, allowing them to be easily and efficiently used and analysed. We explore three strategies--the pathwise, score function, and measure-valued gradient estimators--exploring their historical developments, derivation, and underlying assumptions. We describe their use in other fields, show how they are related and can be combined, and expand on their possible generalisations. Wherever Monte Carlo gradient estimators have been derived and deployed in the past, important advances have followed. A deeper and more widely-held understanding of this problem will lead to further advances, and it is these advances that we wish to support.

Implicit Reparameterization Gradients

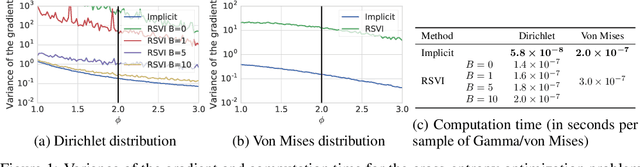
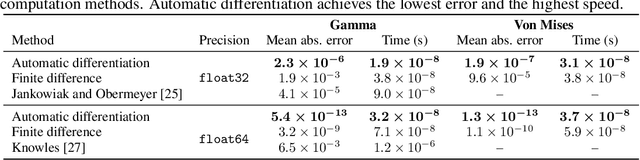
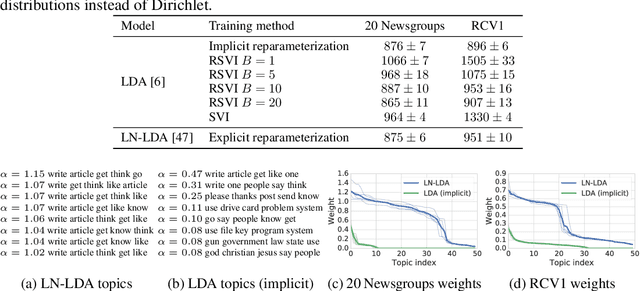
By providing a simple and efficient way of computing low-variance gradients of continuous random variables, the reparameterization trick has become the technique of choice for training a variety of latent variable models. However, it is not applicable to a number of important continuous distributions. We introduce an alternative approach to computing reparameterization gradients based on implicit differentiation and demonstrate its broader applicability by applying it to Gamma, Beta, Dirichlet, and von Mises distributions, which cannot be used with the classic reparameterization trick. Our experiments show that the proposed approach is faster and more accurate than the existing gradient estimators for these distributions.

Universal Conditional Machine

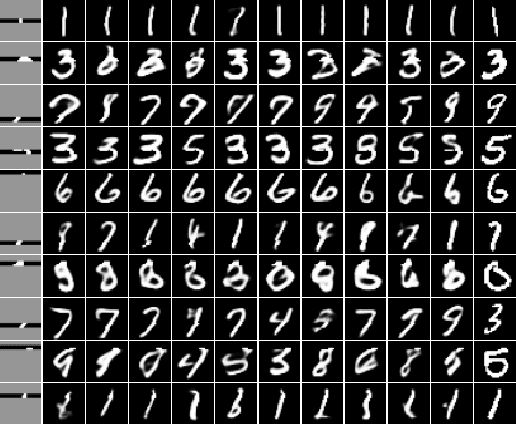
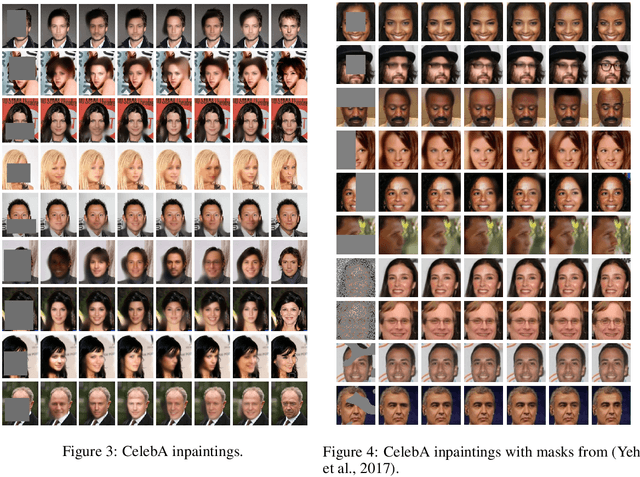
We propose a single neural probabilistic model based on variational autoencoder that can be conditioned on an arbitrary subset of observed features and then sample the remaining features in "one shot". The features may be both real-valued and categorical. Training of the model is performed by stochastic variational Bayes. The experimental evaluation on synthetic data, as well as feature imputation and image inpainting problems, shows the effectiveness of the proposed approach and diversity of the generated samples.

Probabilistic Adaptive Computation Time

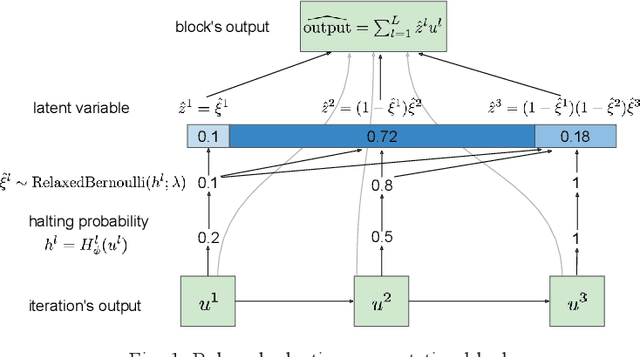
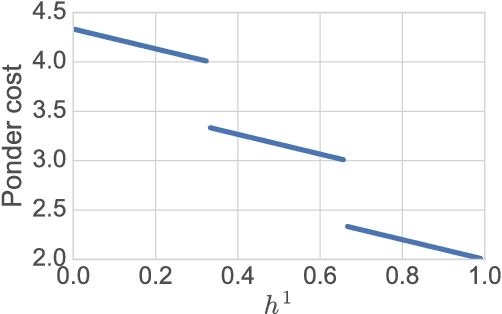
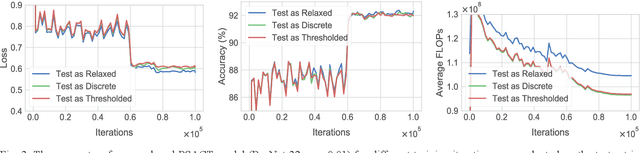
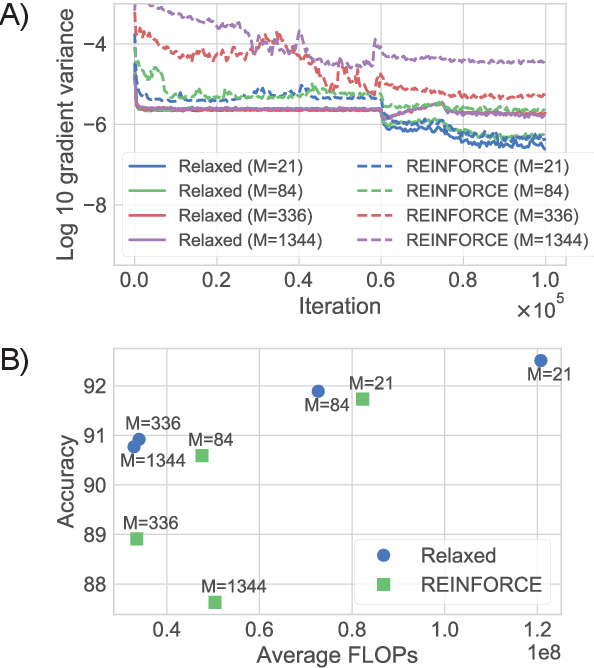
We present a probabilistic model with discrete latent variables that control the computation time in deep learning models such as ResNets and LSTMs. A prior on the latent variables expresses the preference for faster computation. The amount of computation for an input is determined via amortized maximum a posteriori (MAP) inference. MAP inference is performed using a novel stochastic variational optimization method. The recently proposed Adaptive Computation Time mechanism can be seen as an ad-hoc relaxation of this model. We demonstrate training using the general-purpose Concrete relaxation of discrete variables. Evaluation on ResNet shows that our method matches the speed-accuracy trade-off of Adaptive Computation Time, while allowing for evaluation with a simple deterministic procedure that has a lower memory footprint.

Spatially Adaptive Computation Time for Residual Networks

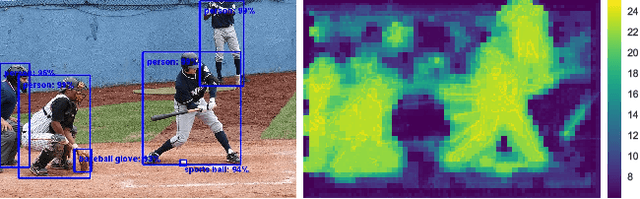
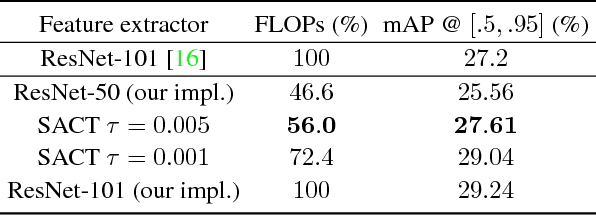
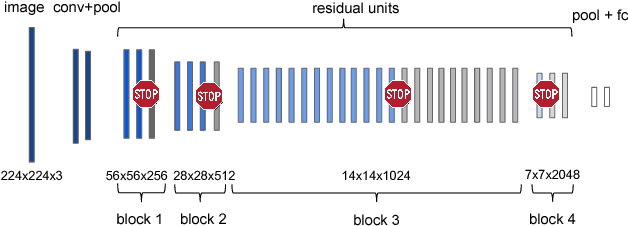
This paper proposes a deep learning architecture based on Residual Network that dynamically adjusts the number of executed layers for the regions of the image. This architecture is end-to-end trainable, deterministic and problem-agnostic. It is therefore applicable without any modifications to a wide range of computer vision problems such as image classification, object detection and image segmentation. We present experimental results showing that this model improves the computational efficiency of Residual Networks on the challenging ImageNet classification and COCO object detection datasets. Additionally, we evaluate the computation time maps on the visual saliency dataset cat2000 and find that they correlate surprisingly well with human eye fixation positions.

Robust Variational Inference

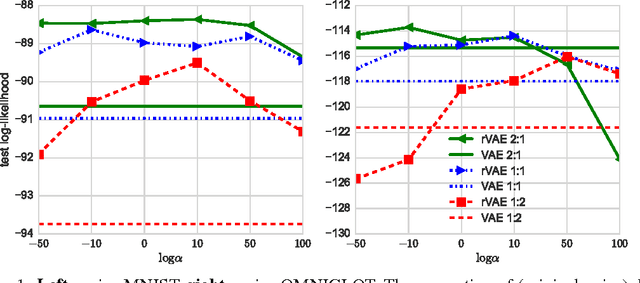
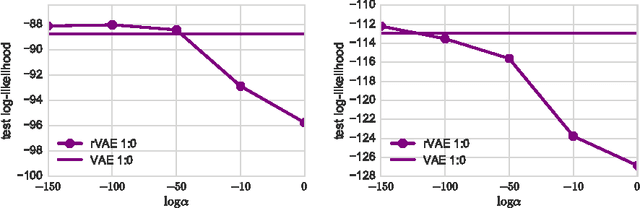
Variational inference is a powerful tool for approximate inference. However, it mainly focuses on the evidence lower bound as variational objective and the development of other measures for variational inference is a promising area of research. This paper proposes a robust modification of evidence and a lower bound for the evidence, which is applicable when the majority of the training set samples are random noise objects. We provide experiments for variational autoencoders to show advantage of the objective over the evidence lower bound on synthetic datasets obtained by adding uninformative noise objects to MNIST and OMNIGLOT. Additionally, for the original MNIST and OMNIGLOT datasets we observe a small improvement over the non-robust evidence lower bound.

PerforatedCNNs: Acceleration through Elimination of Redundant Convolutions

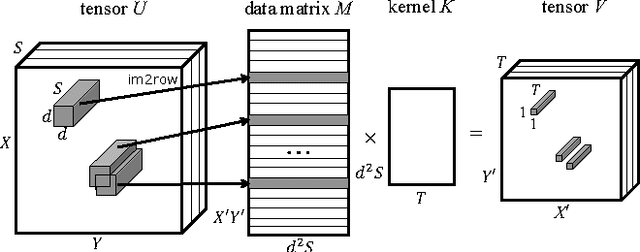
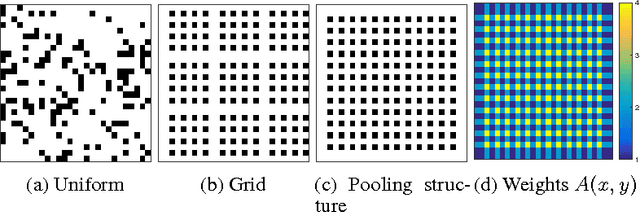
We propose a novel approach to reduce the computational cost of evaluation of convolutional neural networks, a factor that has hindered their deployment in low-power devices such as mobile phones. Inspired by the loop perforation technique from source code optimization, we speed up the bottleneck convolutional layers by skipping their evaluation in some of the spatial positions. We propose and analyze several strategies of choosing these positions. We demonstrate that perforation can accelerate modern convolutional networks such as AlexNet and VGG-16 by a factor of 2x - 4x. Additionally, we show that perforation is complementary to the recently proposed acceleration method of Zhang et al.