Artem Sobolev
Importance Weighted Hierarchical Variational Inference
May 08, 2019


Abstract:Variational Inference is a powerful tool in the Bayesian modeling toolkit, however, its effectiveness is determined by the expressivity of the utilized variational distributions in terms of their ability to match the true posterior distribution. In turn, the expressivity of the variational family is largely limited by the requirement of having a tractable density function. To overcome this roadblock, we introduce a new family of variational upper bounds on a marginal log density in the case of hierarchical models (also known as latent variable models). We then give an upper bound on the Kullback-Leibler divergence and derive a family of increasingly tighter variational lower bounds on the otherwise intractable standard evidence lower bound for hierarchical variational distributions, enabling the use of more expressive approximate posteriors. We show that previously known methods, such as Hierarchical Variational Models, Semi-Implicit Variational Inference and Doubly Semi-Implicit Variational Inference can be seen as special cases of the proposed approach, and empirically demonstrate superior performance of the proposed method in a set of experiments.
Probabilistic Adaptive Computation Time
Dec 01, 2017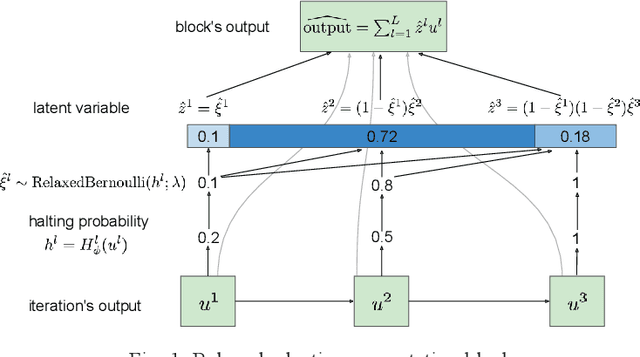
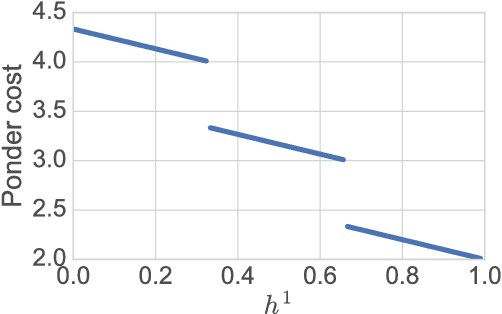
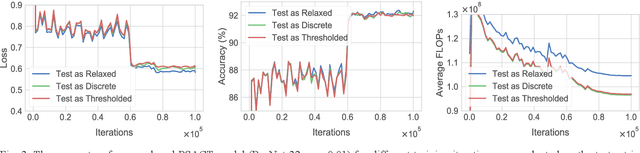
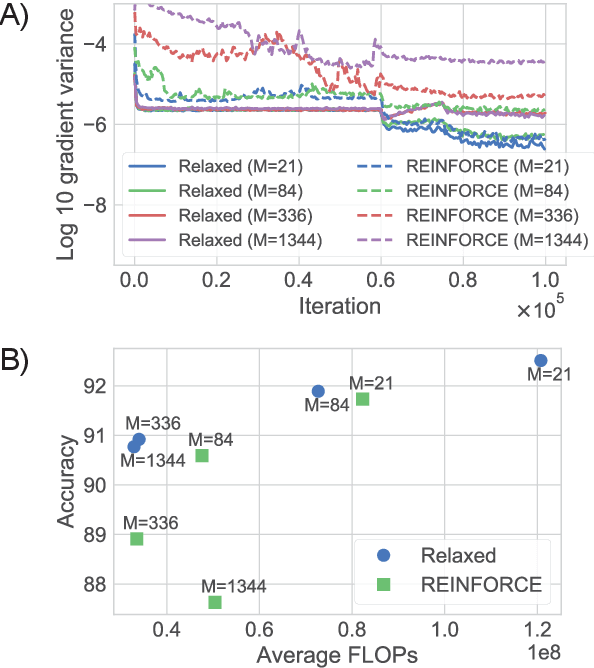
Abstract:We present a probabilistic model with discrete latent variables that control the computation time in deep learning models such as ResNets and LSTMs. A prior on the latent variables expresses the preference for faster computation. The amount of computation for an input is determined via amortized maximum a posteriori (MAP) inference. MAP inference is performed using a novel stochastic variational optimization method. The recently proposed Adaptive Computation Time mechanism can be seen as an ad-hoc relaxation of this model. We demonstrate training using the general-purpose Concrete relaxation of discrete variables. Evaluation on ResNet shows that our method matches the speed-accuracy trade-off of Adaptive Computation Time, while allowing for evaluation with a simple deterministic procedure that has a lower memory footprint.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge