Probabilistic Adaptive Computation Time
Paper and Code
Dec 01, 2017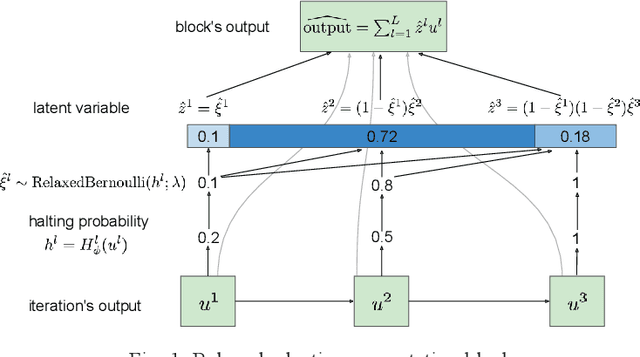
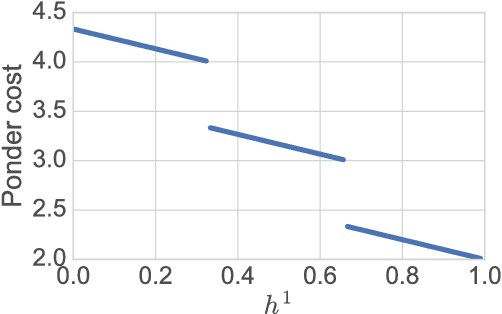
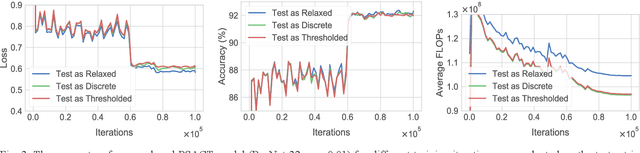
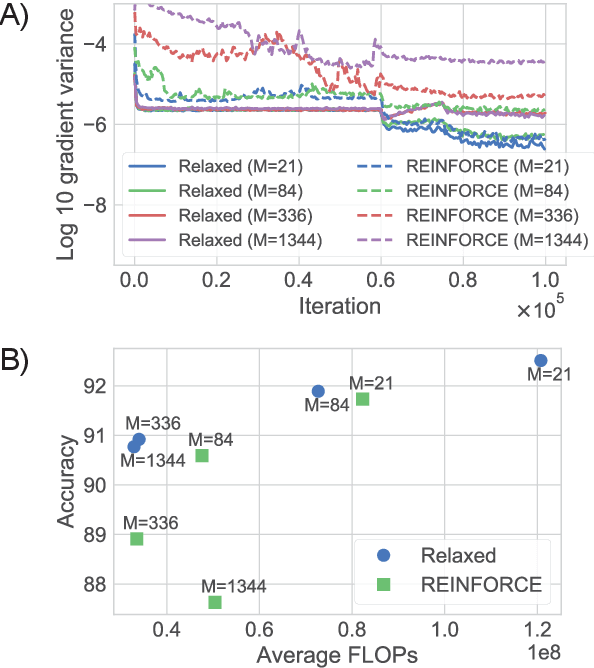
We present a probabilistic model with discrete latent variables that control the computation time in deep learning models such as ResNets and LSTMs. A prior on the latent variables expresses the preference for faster computation. The amount of computation for an input is determined via amortized maximum a posteriori (MAP) inference. MAP inference is performed using a novel stochastic variational optimization method. The recently proposed Adaptive Computation Time mechanism can be seen as an ad-hoc relaxation of this model. We demonstrate training using the general-purpose Concrete relaxation of discrete variables. Evaluation on ResNet shows that our method matches the speed-accuracy trade-off of Adaptive Computation Time, while allowing for evaluation with a simple deterministic procedure that has a lower memory footprint.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge