Goal Agnostic Planning using Maximum Likelihood Paths in Hypergraph World Models

In this paper, we present a hypergraph--based machine learning algorithm, a datastructure--driven maintenance method, and a planning algorithm based on a probabilistic application of Dijkstra's algorithm. Together, these form a goal agnostic automated planning engine for an autonomous learning agent which incorporates beneficial properties of both classical Machine Learning and traditional Artificial Intelligence. We prove that the algorithm determines optimal solutions within the problem space, mathematically bound learning performance, and supply a mathematical model analyzing system state progression through time yielding explicit predictions for learning curves, goal achievement rates, and response to abstractions and uncertainty. To validate performance, we exhibit results from applying the agent to three archetypal planning problems, including composite hierarchical domains, and highlight empirical findings which illustrate properties elucidated in the analysis.

Low-variance Black-box Gradient Estimates for the Plackett-Luce Distribution

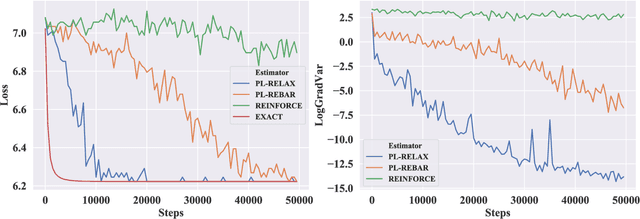
Learning models with discrete latent variables using stochastic gradient descent remains a challenge due to the high variance of gradient estimates. Modern variance reduction techniques mostly consider categorical distributions and have limited applicability when the number of possible outcomes becomes large. In this work, we consider models with latent permutations and propose control variates for the Plackett-Luce distribution. In particular, the control variates allow us to optimize black-box functions over permutations using stochastic gradient descent. To illustrate the approach, we consider a variety of causal structure learning tasks for continuous and discrete data. We show that our method outperforms competitive relaxation-based optimization methods and is also applicable to non-differentiable score functions.