Scalable Simulation-free Entropic Unbalanced Optimal Transport
Paper and Code
Oct 03, 2024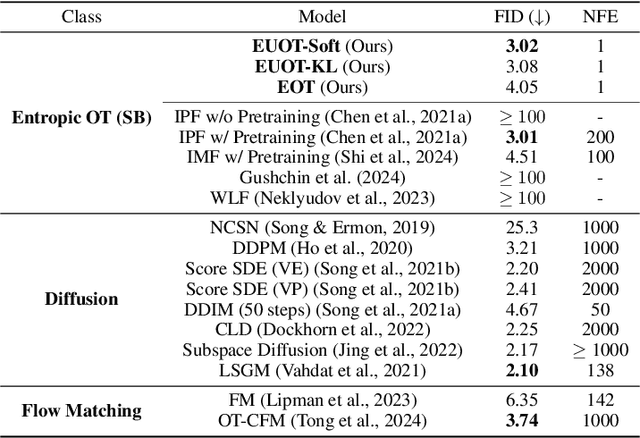


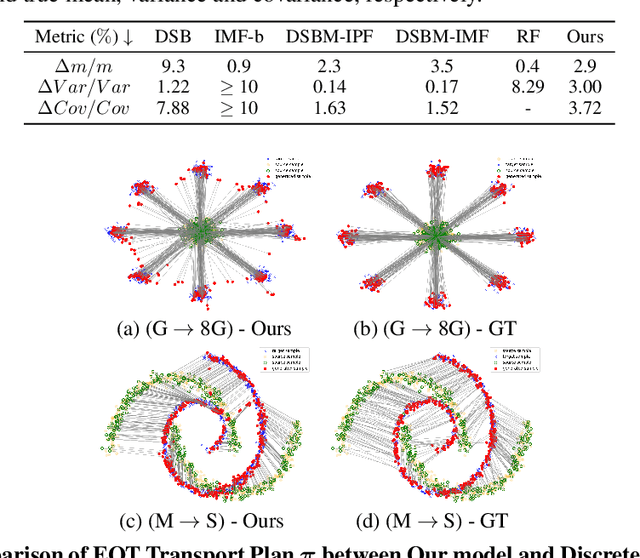
The Optimal Transport (OT) problem investigates a transport map that connects two distributions while minimizing a given cost function. Finding such a transport map has diverse applications in machine learning, such as generative modeling and image-to-image translation. In this paper, we introduce a scalable and simulation-free approach for solving the Entropic Unbalanced Optimal Transport (EUOT) problem. We derive the dynamical form of this EUOT problem, which is a generalization of the Schr\"odinger bridges (SB) problem. Based on this, we derive dual formulation and optimality conditions of the EUOT problem from the stochastic optimal control interpretation. By leveraging these properties, we propose a simulation-free algorithm to solve EUOT, called Simulation-free EUOT (SF-EUOT). While existing SB models require expensive simulation costs during training and evaluation, our model achieves simulation-free training and one-step generation by utilizing the reciprocal property. Our model demonstrates significantly improved scalability in generative modeling and image-to-image translation tasks compared to previous SB methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge