Improving Neural Optimal Transport via Displacement Interpolation
Paper and Code
Oct 03, 2024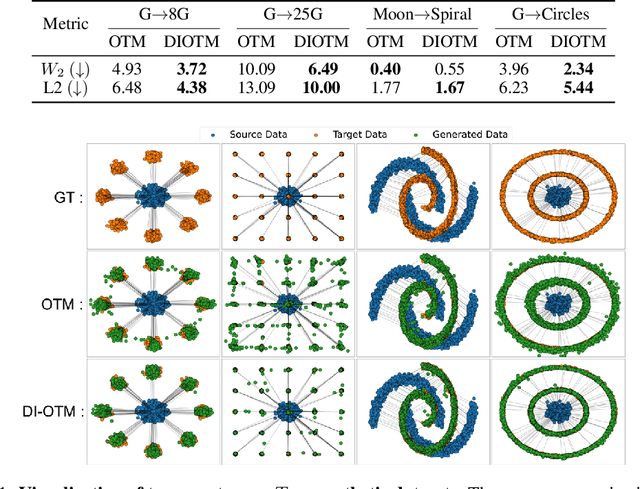

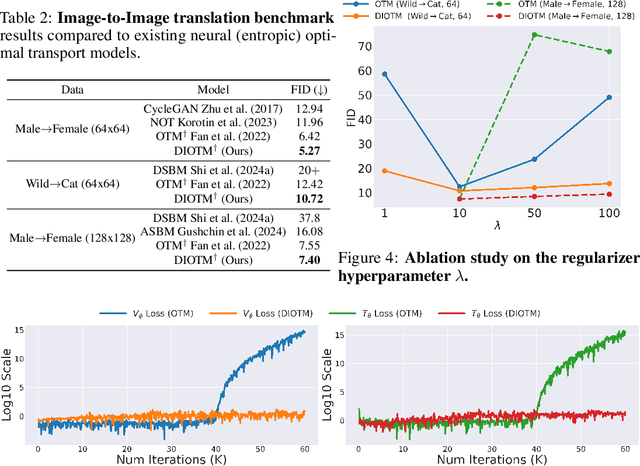

Optimal Transport (OT) theory investigates the cost-minimizing transport map that moves a source distribution to a target distribution. Recently, several approaches have emerged for learning the optimal transport map for a given cost function using neural networks. We refer to these approaches as the OT Map. OT Map provides a powerful tool for diverse machine learning tasks, such as generative modeling and unpaired image-to-image translation. However, existing methods that utilize max-min optimization often experience training instability and sensitivity to hyperparameters. In this paper, we propose a novel method to improve stability and achieve a better approximation of the OT Map by exploiting displacement interpolation, dubbed Displacement Interpolation Optimal Transport Model (DIOTM). We derive the dual formulation of displacement interpolation at specific time $t$ and prove how these dual problems are related across time. This result allows us to utilize the entire trajectory of displacement interpolation in learning the OT Map. Our method improves the training stability and achieves superior results in estimating optimal transport maps. We demonstrate that DIOTM outperforms existing OT-based models on image-to-image translation tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge