Boumediene Hamzi
Kernel Methods for the Approximation of the Eigenfunctions of the Koopman Operator
Dec 21, 2024



Abstract:The Koopman operator provides a linear framework to study nonlinear dynamical systems. Its spectra offer valuable insights into system dynamics, but the operator can exhibit both discrete and continuous spectra, complicating direct computations. In this paper, we introduce a kernel-based method to construct the principal eigenfunctions of the Koopman operator without explicitly computing the operator itself. These principal eigenfunctions are associated with the equilibrium dynamics, and their eigenvalues match those of the linearization of the nonlinear system at the equilibrium point. We exploit the structure of the principal eigenfunctions by decomposing them into linear and nonlinear components. The linear part corresponds to the left eigenvector of the system's linearization at the equilibrium, while the nonlinear part is obtained by solving a partial differential equation (PDE) using kernel methods. Our approach avoids common issues such as spectral pollution and spurious eigenvalues, which can arise in previous methods. We demonstrate the effectiveness of our algorithm through numerical examples.
Kernel Sum of Squares for Data Adapted Kernel Learning of Dynamical Systems from Data: A global optimization approach
Aug 12, 2024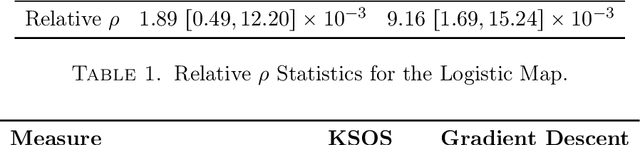
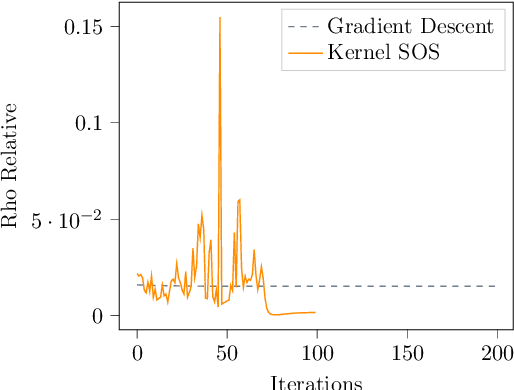

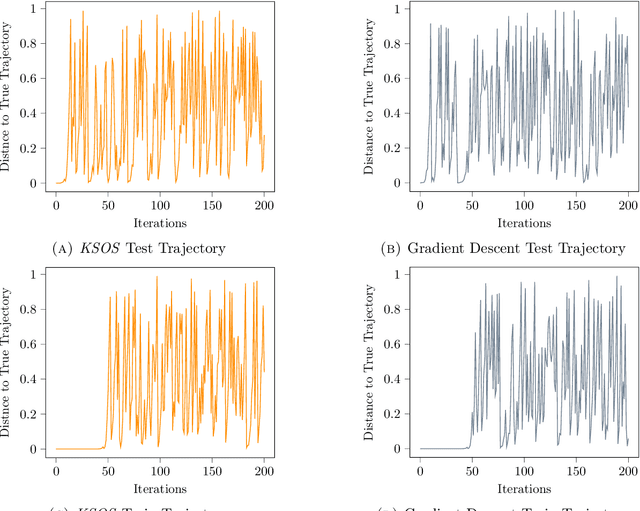
Abstract:This paper examines the application of the Kernel Sum of Squares (KSOS) method for enhancing kernel learning from data, particularly in the context of dynamical systems. Traditional kernel-based methods, despite their theoretical soundness and numerical efficiency, frequently struggle with selecting optimal base kernels and parameter tuning, especially with gradient-based methods prone to local optima. KSOS mitigates these issues by leveraging a global optimization framework with kernel-based surrogate functions, thereby achieving more reliable and precise learning of dynamical systems. Through comprehensive numerical experiments on the Logistic Map, Henon Map, and Lorentz System, KSOS is shown to consistently outperform gradient descent in minimizing the relative-$\rho$ metric and improving kernel accuracy. These results highlight KSOS's effectiveness in predicting the behavior of chaotic dynamical systems, demonstrating its capability to adapt kernels to underlying dynamics and enhance the robustness and predictive power of kernel-based approaches, making it a valuable asset for time series analysis in various scientific fields.
Simplicity bias, algorithmic probability, and the random logistic map
Dec 31, 2023


Abstract:Simplicity bias is an intriguing phenomenon prevalent in various input-output maps, characterized by a preference for simpler, more regular, or symmetric outputs. Notably, these maps typically feature high-probability outputs with simple patterns, whereas complex patterns are exponentially less probable. This bias has been extensively examined and attributed to principles derived from algorithmic information theory and algorithmic probability. In a significant advancement, it has been demonstrated that the renowned logistic map $x_{k+1}=\mu x_k(1-x_k)$, and other one-dimensional maps exhibit simplicity bias when conceptualized as input-output systems. Building upon this foundational work, our research delves into the manifestations of simplicity bias within the random logistic map, specifically focusing on scenarios involving additive noise. This investigation is driven by the overarching goal of formulating a comprehensive theory for the prediction and analysis of time series.Our primary contributions are multifaceted. We discover that simplicity bias is observable in the random logistic map for specific ranges of $\mu$ and noise magnitudes. Additionally, we find that this bias persists even with the introduction of small measurement noise, though it diminishes as noise levels increase. Our studies also revisit the phenomenon of noise-induced chaos, particularly when $\mu=3.83$, revealing its characteristics through complexity-probability plots. Intriguingly, we employ the logistic map to underscore a paradoxical aspect of data analysis: more data adhering to a consistent trend can occasionally lead to reduced confidence in extrapolation predictions, challenging conventional wisdom.We propose that adopting a probability-complexity perspective in analyzing dynamical systems could significantly enrich statistical learning theories related to series prediction.
Bridging Algorithmic Information Theory and Machine Learning: A New Approach to Kernel Learning
Nov 21, 2023Abstract:Machine Learning (ML) and Algorithmic Information Theory (AIT) look at Complexity from different points of view. We explore the interface between AIT and Kernel Methods (that are prevalent in ML) by adopting an AIT perspective on the problem of learning kernels from data, in kernel ridge regression, through the method of Sparse Kernel Flows. In particular, by looking at the differences and commonalities between Minimal Description Length (MDL) and Regularization in Machine Learning (RML), we prove that the method of Sparse Kernel Flows is the natural approach to adopt to learn kernels from data. This paper shows that it is not necessary to use the statistical route to derive Sparse Kernel Flows and that one can directly work with code-lengths and complexities that are concepts that show up in AIT.
Learning Dynamical Systems from Data: A Simple Cross-Validation Perspective, Part V: Sparse Kernel Flows for 132 Chaotic Dynamical Systems
Jan 24, 2023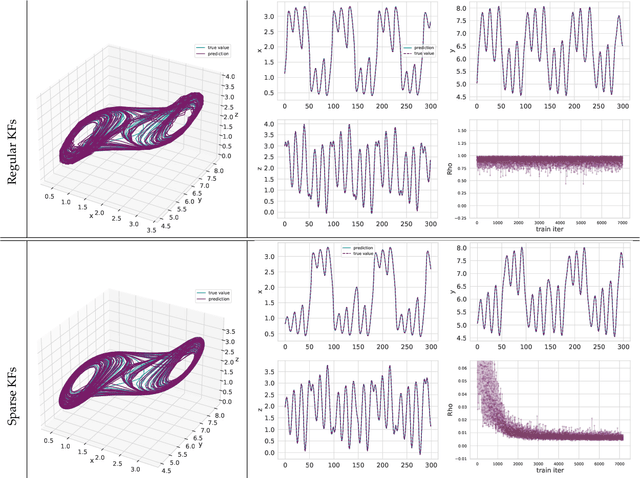

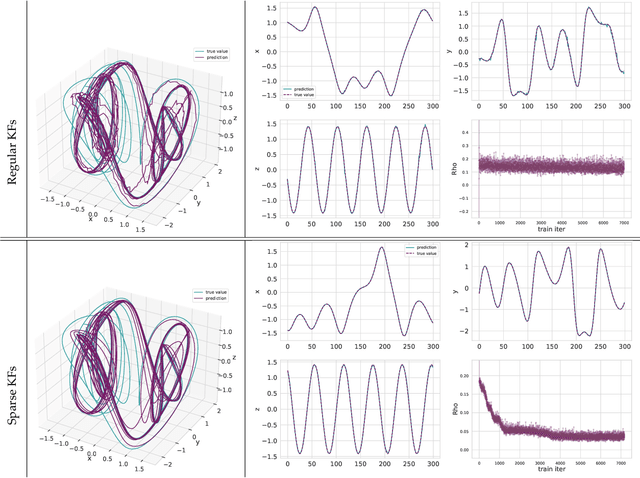
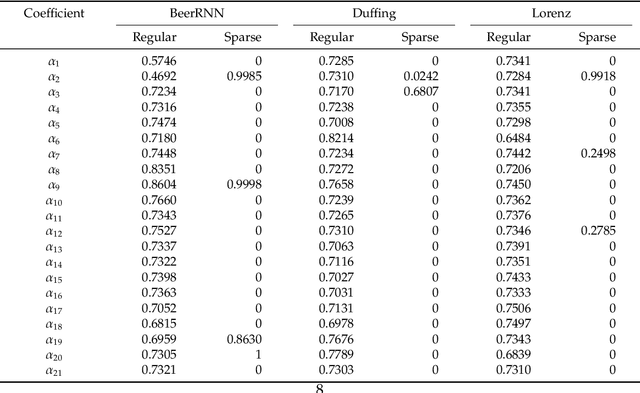
Abstract:Regressing the vector field of a dynamical system from a finite number of observed states is a natural way to learn surrogate models for such systems. A simple and interpretable way to learn a dynamical system from data is to interpolate its vector-field with a data-adapted kernel which can be learned by using Kernel Flows. The method of Kernel Flows is a trainable machine learning method that learns the optimal parameters of a kernel based on the premise that a kernel is good if there is no significant loss in accuracy if half of the data is used. The objective function could be a short-term prediction or some other objective for other variants of Kernel Flows). However, this method is limited by the choice of the base kernel. In this paper, we introduce the method of \emph{Sparse Kernel Flows } in order to learn the ``best'' kernel by starting from a large dictionary of kernels. It is based on sparsifying a kernel that is a linear combination of elemental kernels. We apply this approach to a library of 132 chaotic systems.
One-Shot Learning of Stochastic Differential Equations with Computational Graph Completion
Sep 24, 2022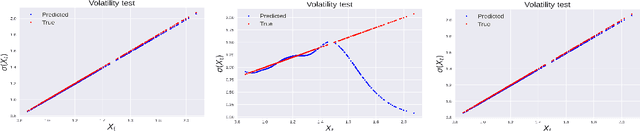

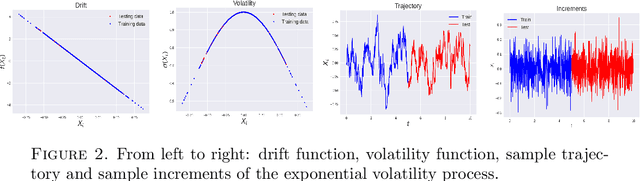

Abstract:We consider the problem of learning Stochastic Differential Equations of the form $dX_t = f(X_t)dt+\sigma(X_t)dW_t $ from one sample trajectory. This problem is more challenging than learning deterministic dynamical systems because one sample trajectory only provides indirect information on the unknown functions $f$, $\sigma$, and stochastic process $dW_t$ representing the drift, the diffusion, and the stochastic forcing terms, respectively. We propose a simple kernel-based solution to this problem that can be decomposed as follows: (1) Represent the time-increment map $X_t \rightarrow X_{t+dt}$ as a Computational Graph in which $f$, $\sigma$ and $dW_t$ appear as unknown functions and random variables. (2) Complete the graph (approximate unknown functions and random variables) via Maximum a Posteriori Estimation (given the data) with Gaussian Process (GP) priors on the unknown functions. (3) Learn the covariance functions (kernels) of the GP priors from data with randomized cross-validation. Numerical experiments illustrate the efficacy, robustness, and scope of our method.
Learning dynamical systems from data: A simple cross-validation perspective, part III: Irregularly-Sampled Time Series
Nov 25, 2021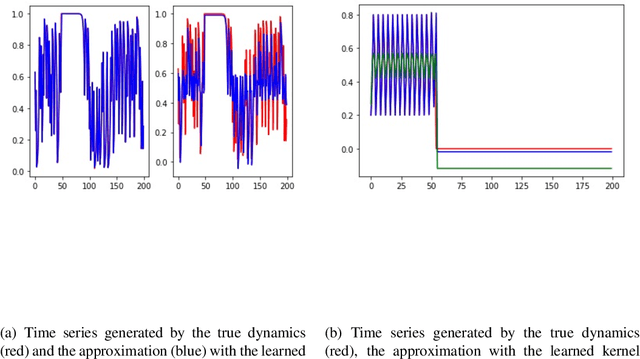
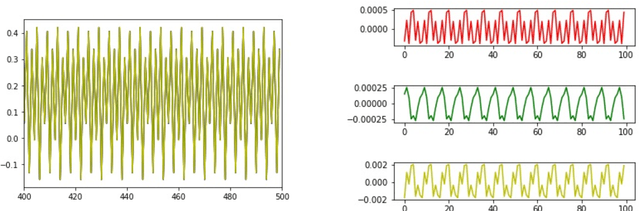

Abstract:A simple and interpretable way to learn a dynamical system from data is to interpolate its vector-field with a kernel. In particular, this strategy is highly efficient (both in terms of accuracy and complexity) when the kernel is data-adapted using Kernel Flows (KF)~\cite{Owhadi19} (which uses gradient-based optimization to learn a kernel based on the premise that a kernel is good if there is no significant loss in accuracy if half of the data is used for interpolation). Despite its previous successes, this strategy (based on interpolating the vector field driving the dynamical system) breaks down when the observed time series is not regularly sampled in time. In this work, we propose to address this problem by directly approximating the vector field of the dynamical system by incorporating time differences between observations in the (KF) data-adapted kernels. We compare our approach with the classical one over different benchmark dynamical systems and show that it significantly improves the forecasting accuracy while remaining simple, fast, and robust.
Kernel methods for center manifold approximation and a data-based version of the Center Manifold Theorem
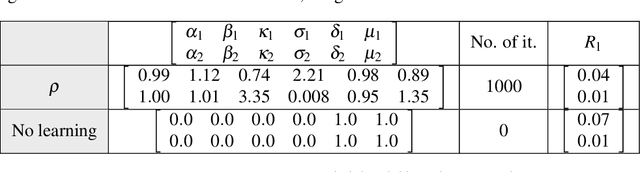
Dec 01, 2020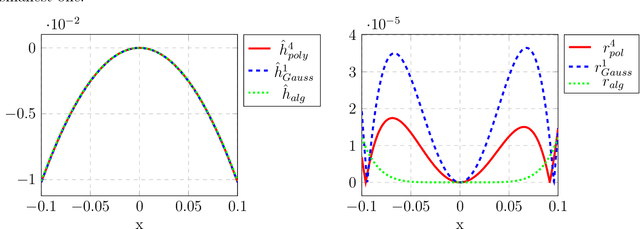
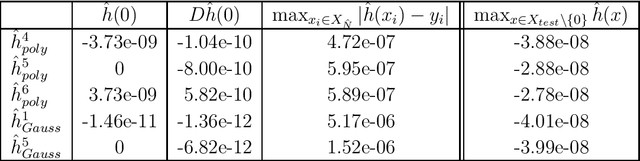

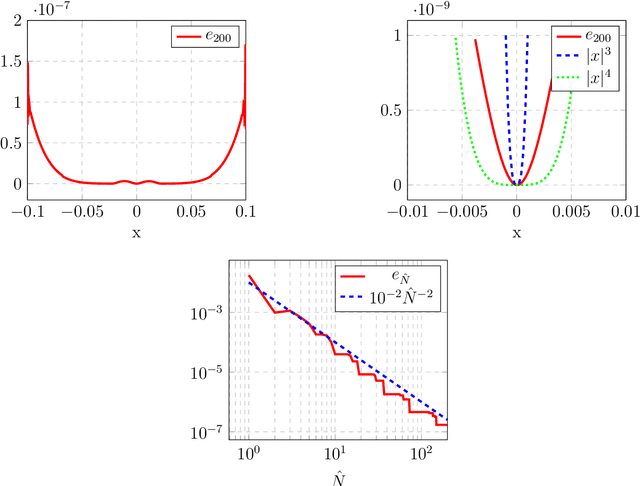
Abstract:For dynamical systems with a non hyperbolic equilibrium, it is possible to significantly simplify the study of stability by means of the center manifold theory. This theory allows to isolate the complicated asymptotic behavior of the system close to the equilibrium point and to obtain meaningful predictions of its behavior by analyzing a reduced order system on the so-called center manifold. Since the center manifold is usually not known, good approximation methods are important as the center manifold theorem states that the stability properties of the origin of the reduced order system are the same as those of the origin of the full order system. In this work, we establish a data-based version of the center manifold theorem that works by considering an approximation in place of an exact manifold. Also the error between the approximated and the original reduced dynamics are quantified. We then use an apposite data-based kernel method to construct a suitable approximation of the manifold close to the equilibrium, which is compatible with our general error theory. The data are collected by repeated numerical simulation of the full system by means of a high-accuracy solver, which generates sets of discrete trajectories that are then used as a training set. The method is tested on different examples which show promising performance and good accuracy.
Learning dynamical systems from data: a simple cross-validation perspective
Jul 09, 2020



Abstract:Regressing the vector field of a dynamical system from a finite number of observed states is a natural way to learn surrogate models for such systems. We present variants of cross-validation (Kernel Flows \cite{Owhadi19} and its variants based on Maximum Mean Discrepancy and Lyapunov exponents) as simple approaches for learning the kernel used in these emulators.
Kernel-based approximation of the Koopman generator and Schrödinger operator
Jun 25, 2020



Abstract:Many dimensionality and model reduction techniques rely on estimating dominant eigenfunctions of associated dynamical operators from data. Important examples include the Koopman operator and its generator, but also the Schr\"odinger operator. We propose a kernel-based method for the approximation of differential operators in reproducing kernel Hilbert spaces and show how eigenfunctions can be estimated by solving auxiliary matrix eigenvalue problems. The resulting algorithms are applied to molecular dynamics and quantum chemistry examples. Furthermore, we exploit that, under certain conditions, the Schr\"odinger operator can be transformed into a Kolmogorov backward operator corresponding to a drift-diffusion process and vice versa. This allows us to apply methods developed for the analysis of high-dimensional stochastic differential equations to quantum mechanical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge