Kernel Sum of Squares for Data Adapted Kernel Learning of Dynamical Systems from Data: A global optimization approach
Paper and Code
Aug 12, 2024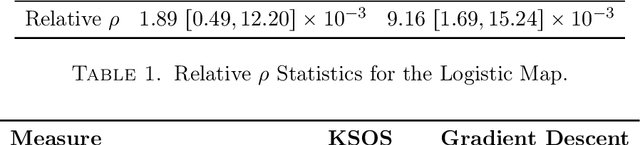
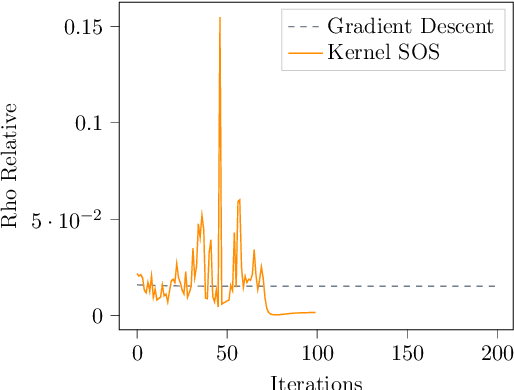

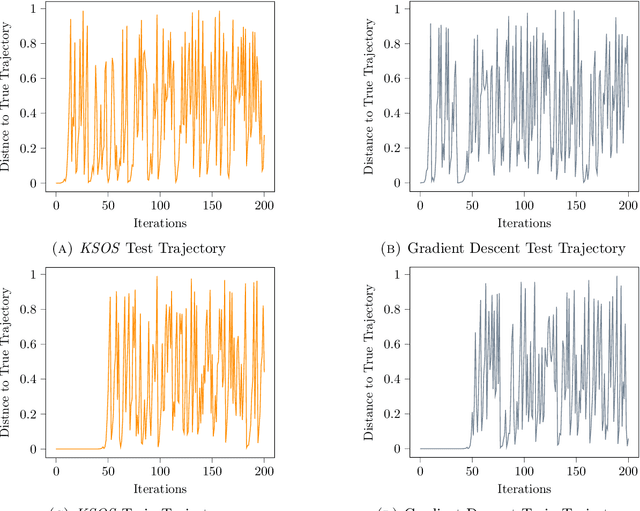
This paper examines the application of the Kernel Sum of Squares (KSOS) method for enhancing kernel learning from data, particularly in the context of dynamical systems. Traditional kernel-based methods, despite their theoretical soundness and numerical efficiency, frequently struggle with selecting optimal base kernels and parameter tuning, especially with gradient-based methods prone to local optima. KSOS mitigates these issues by leveraging a global optimization framework with kernel-based surrogate functions, thereby achieving more reliable and precise learning of dynamical systems. Through comprehensive numerical experiments on the Logistic Map, Henon Map, and Lorentz System, KSOS is shown to consistently outperform gradient descent in minimizing the relative-$\rho$ metric and improving kernel accuracy. These results highlight KSOS's effectiveness in predicting the behavior of chaotic dynamical systems, demonstrating its capability to adapt kernels to underlying dynamics and enhance the robustness and predictive power of kernel-based approaches, making it a valuable asset for time series analysis in various scientific fields.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge