Kernel Sum of Squares for Data Adapted Kernel Learning of Dynamical Systems from Data: A global optimization approach

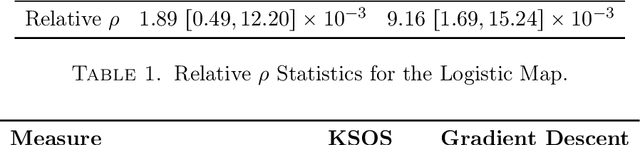
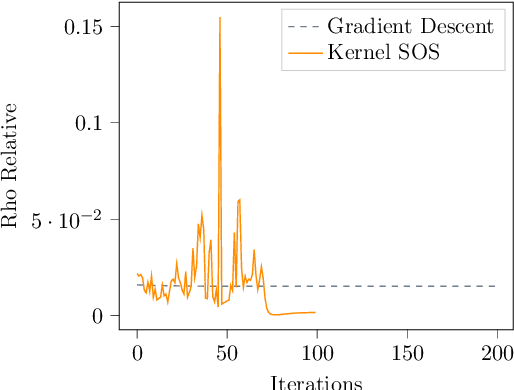
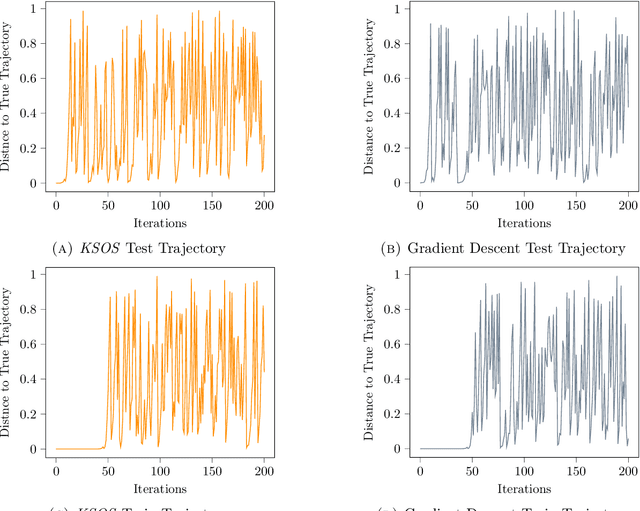
This paper examines the application of the Kernel Sum of Squares (KSOS) method for enhancing kernel learning from data, particularly in the context of dynamical systems. Traditional kernel-based methods, despite their theoretical soundness and numerical efficiency, frequently struggle with selecting optimal base kernels and parameter tuning, especially with gradient-based methods prone to local optima. KSOS mitigates these issues by leveraging a global optimization framework with kernel-based surrogate functions, thereby achieving more reliable and precise learning of dynamical systems. Through comprehensive numerical experiments on the Logistic Map, Henon Map, and Lorentz System, KSOS is shown to consistently outperform gradient descent in minimizing the relative-$\rho$ metric and improving kernel accuracy. These results highlight KSOS's effectiveness in predicting the behavior of chaotic dynamical systems, demonstrating its capability to adapt kernels to underlying dynamics and enhance the robustness and predictive power of kernel-based approaches, making it a valuable asset for time series analysis in various scientific fields.

Privacy Risk for anisotropic Langevin dynamics using relative entropy bounds

The privacy preserving properties of Langevin dynamics with additive isotropic noise have been extensively studied. However, the isotropic noise assumption is very restrictive: (a) when adding noise to existing learning algorithms to preserve privacy and maintain the best possible accuracy one should take into account the relative magnitude of the outputs and their correlations; (b) popular algorithms such as stochastic gradient descent (and their continuous time limits) appear to possess anisotropic covariance properties. To study the privacy risks for the anisotropic noise case, one requires general results on the relative entropy between the laws of two Stochastic Differential Equations with different drifts and diffusion coefficients. Our main contribution is to establish such a bound using stability estimates for solutions to the Fokker-Planck equations via functional inequalities. With additional assumptions, the relative entropy bound implies an $(\epsilon,\delta)$-differential privacy bound. We discuss the practical implications of our bound related to privacy risk in different contexts.Finally, the benefits of anisotropic noise are illustrated using numerical results on optimising a quadratic loss or calibrating a neural network.

Data-driven initialization of deep learning solvers for Hamilton-Jacobi-Bellman PDEs

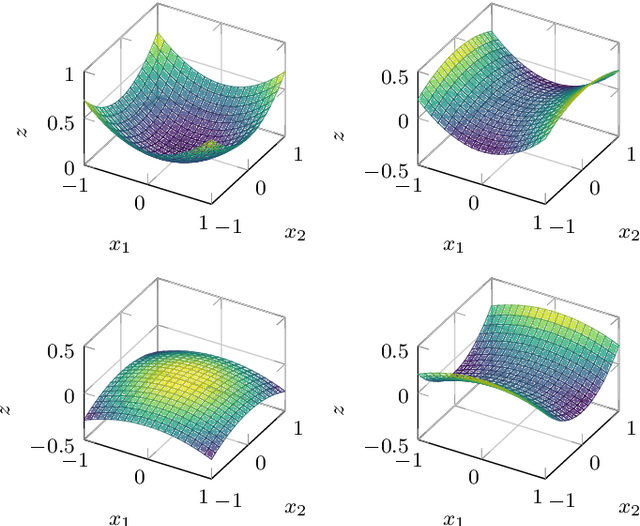
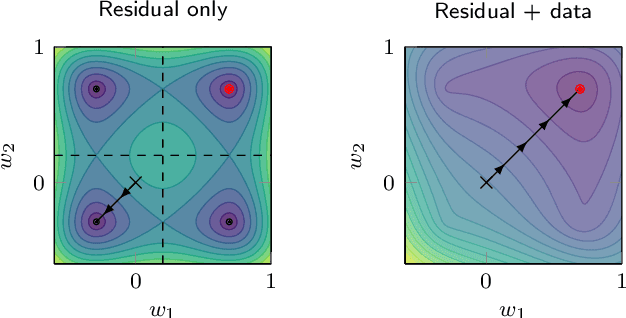
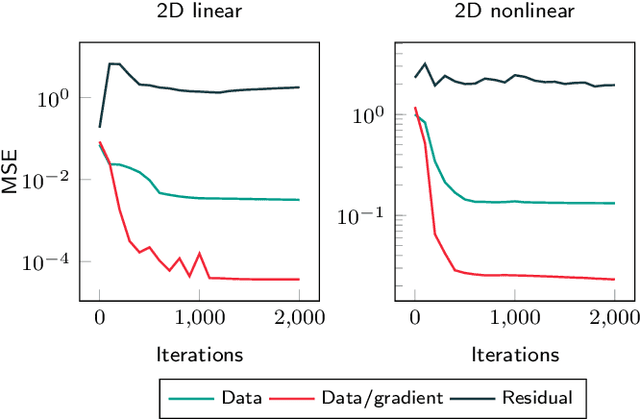
A deep learning approach for the approximation of the Hamilton-Jacobi-Bellman partial differential equation (HJB PDE) associated to the Nonlinear Quadratic Regulator (NLQR) problem. A state-dependent Riccati equation control law is first used to generate a gradient-augmented synthetic dataset for supervised learning. The resulting model becomes a warm start for the minimization of a loss function based on the residual of the HJB PDE. The combination of supervised learning and residual minimization avoids spurious solutions and mitigate the data inefficiency of a supervised learning-only approach. Numerical tests validate the different advantages of the proposed methodology.

On stochastic mirror descent with interacting particles: convergence properties and variance reduction

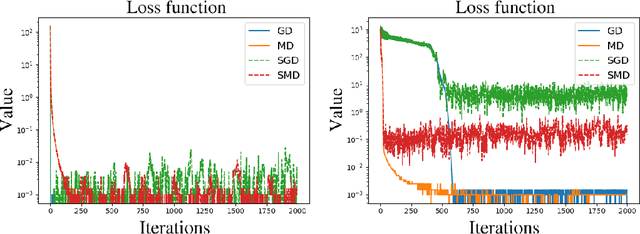
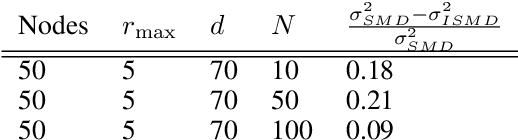
An open problem in optimization with noisy information is the computation of an exact minimizer that is independent of the amount of noise. A standard practice in stochastic approximation algorithms is to use a decreasing step-size. However, to converge the step-size must decrease exponentially slow, and therefore this approach is not useful in practice. A second alternative is to use a fixed step-size and run independent replicas of the algorithm and average these. A third option is to run replicas of the algorithm and allow them to interact. It is unclear which of these options works best. To address this question, we reduce the problem of the computation of an exact minimizer with noisy gradient information to the study of stochastic mirror descent with interacting particles. We study the convergence of stochastic mirror descent and make explicit the tradeoffs between communication and variance reduction. We provide theoretical and numerical evidence to suggest that interaction helps to improve convergence and reduce the variance of the estimate.

Towards Robust and Stable Deep Learning Algorithms for Forward Backward Stochastic Differential Equations

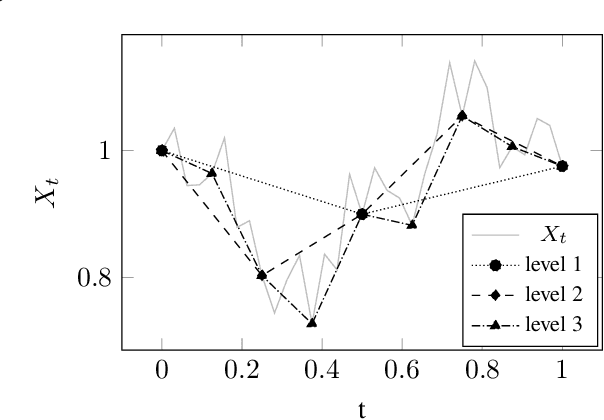
Applications in quantitative finance such as optimal trade execution, risk management of options, and optimal asset allocation involve the solution of high dimensional and nonlinear Partial Differential Equations (PDEs). The connection between PDEs and systems of Forward-Backward Stochastic Differential Equations (FBSDEs) enables the use of advanced simulation techniques to be applied even in the high dimensional setting. Unfortunately, when the underlying application contains nonlinear terms, then classical methods both for simulation and numerical methods for PDEs suffer from the curse of dimensionality. Inspired by the success of deep learning, several researchers have recently proposed to address the solution of FBSDEs using deep learning. We discuss the dynamical systems point of view of deep learning and compare several architectures in terms of stability, generalization, and robustness. In order to speed up the computations, we propose to use a multilevel discretization technique. Our preliminary results suggest that the multilevel discretization method improves solutions times by an order of magnitude compared to existing methods without sacrificing stability or robustness.

The sharp, the flat and the shallow: Can weakly interacting agents learn to escape bad minima?

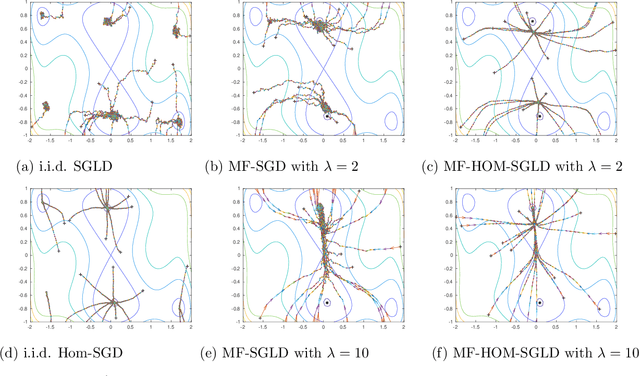
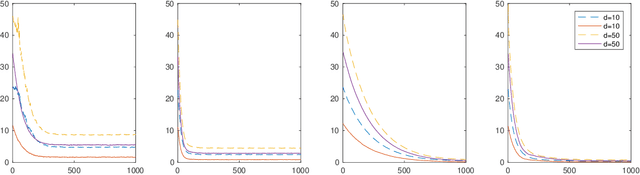
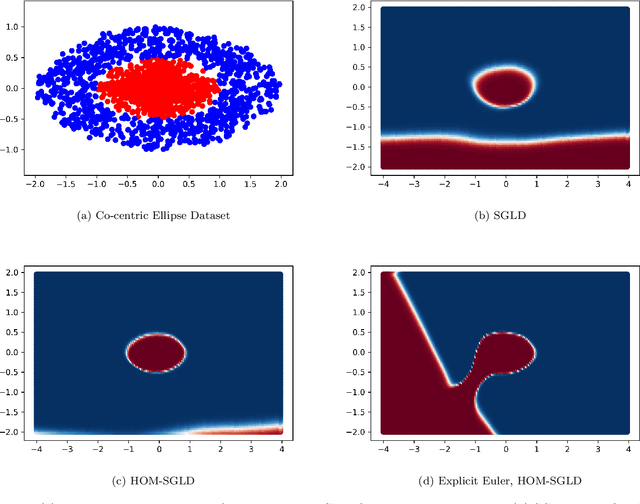
An open problem in machine learning is whether flat minima generalize better and how to compute such minima efficiently. This is a very challenging problem. As a first step towards understanding this question we formalize it as an optimization problem with weakly interacting agents. We review appropriate background material from the theory of stochastic processes and provide insights that are relevant to practitioners. We propose an algorithmic framework for an extended stochastic gradient Langevin dynamics and illustrate its potential. The paper is written as a tutorial, and presents an alternative use of multi-agent learning. Our primary focus is on the design of algorithms for machine learning applications; however the underlying mathematical framework is suitable for the understanding of large scale systems of agent based models that are popular in the social sciences, economics and finance.

Predict Globally, Correct Locally: Parallel-in-Time Optimal Control of Neural Networks

The links between optimal control of dynamical systems and neural networks have proved beneficial both from a theoretical and from a practical point of view. Several researchers have exploited these links to investigate the stability of different neural network architectures and develop memory efficient training algorithms. We also adopt the dynamical systems view of neural networks, but our aim is different from earlier works. We exploit the links between dynamical systems, optimal control, and neural networks to develop a novel distributed optimization algorithm. The proposed algorithm addresses the most significant obstacle for distributed algorithms for neural network optimization: the network weights cannot be updated until the forward propagation of the data, and backward propagation of the gradients are complete. Using the dynamical systems point of view, we interpret the layers of a (residual) neural network as the discretized dynamics of a dynamical system and exploit the relationship between the co-states (adjoints) of the optimal control problem and backpropagation. We then develop a parallel-in-time method that updates the parameters of the network without waiting for the forward or back propagation algorithms to complete in full. We establish the convergence of the proposed algorithm. Preliminary numerical results suggest that the algorithm is competitive and more efficient than the state-of-the-art.

MAGMA: Multi-level accelerated gradient mirror descent algorithm for large-scale convex composite minimization

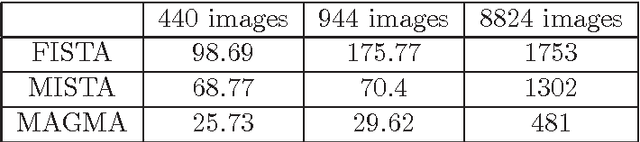
Composite convex optimization models arise in several applications, and are especially prevalent in inverse problems with a sparsity inducing norm and in general convex optimization with simple constraints. The most widely used algorithms for convex composite models are accelerated first order methods, however they can take a large number of iterations to compute an acceptable solution for large-scale problems. In this paper we propose to speed up first order methods by taking advantage of the structure present in many applications and in image processing in particular. Our method is based on multi-level optimization methods and exploits the fact that many applications that give rise to large scale models can be modelled using varying degrees of fidelity. We use Nesterov's acceleration techniques together with the multi-level approach to achieve $\mathcal{O}(1/\sqrt{\epsilon})$ convergence rate, where $\epsilon$ denotes the desired accuracy. The proposed method has a better convergence rate than any other existing multi-level method for convex problems, and in addition has the same rate as accelerated methods, which is known to be optimal for first-order methods. Moreover, as our numerical experiments show, on large-scale face recognition problems our algorithm is several times faster than the state of the art.