Vahan Hovhannisyan
Form follows Function: Text-to-Text Conditional Graph Generation based on Functional Requirements
Nov 01, 2023Abstract:This work focuses on the novel problem setting of generating graphs conditioned on a description of the graph's functional requirements in a downstream task. We pose the problem as a text-to-text generation problem and focus on the approach of fine-tuning a pretrained large language model (LLM) to generate graphs. We propose an inductive bias which incorporates information about the structure of the graph into the LLM's generation process by incorporating message passing layers into an LLM's architecture. To evaluate our proposed method, we design a novel set of experiments using publicly available and widely studied molecule and knowledge graph data sets. Results suggest our proposed approach generates graphs which more closely meet the requested functional requirements, outperforming baselines developed on similar tasks by a statistically significant margin.
MAGMA: Multi-level accelerated gradient mirror descent algorithm for large-scale convex composite minimization
Jul 14, 2016

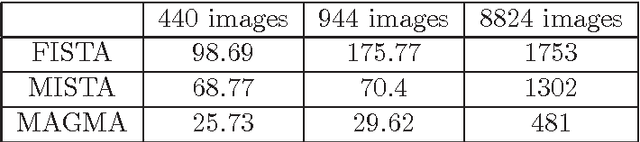

Abstract:Composite convex optimization models arise in several applications, and are especially prevalent in inverse problems with a sparsity inducing norm and in general convex optimization with simple constraints. The most widely used algorithms for convex composite models are accelerated first order methods, however they can take a large number of iterations to compute an acceptable solution for large-scale problems. In this paper we propose to speed up first order methods by taking advantage of the structure present in many applications and in image processing in particular. Our method is based on multi-level optimization methods and exploits the fact that many applications that give rise to large scale models can be modelled using varying degrees of fidelity. We use Nesterov's acceleration techniques together with the multi-level approach to achieve $\mathcal{O}(1/\sqrt{\epsilon})$ convergence rate, where $\epsilon$ denotes the desired accuracy. The proposed method has a better convergence rate than any other existing multi-level method for convex problems, and in addition has the same rate as accelerated methods, which is known to be optimal for first-order methods. Moreover, as our numerical experiments show, on large-scale face recognition problems our algorithm is several times faster than the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge