Deep Unlearn: Benchmarking Machine Unlearning

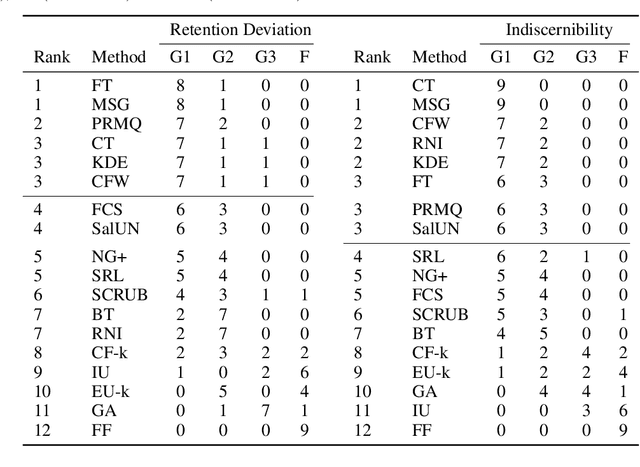
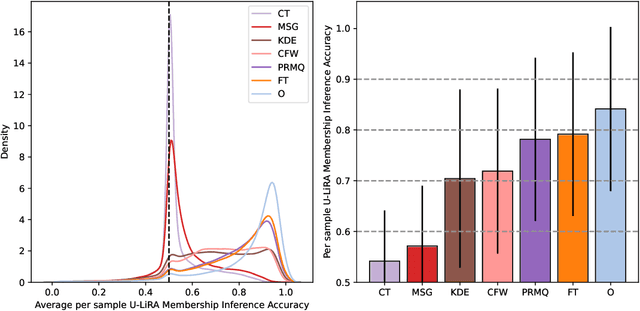
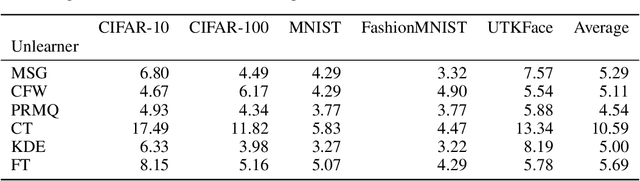
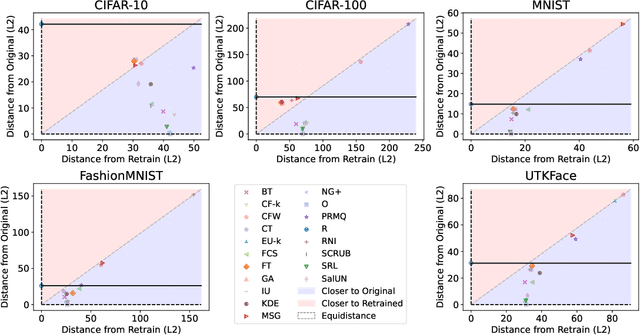
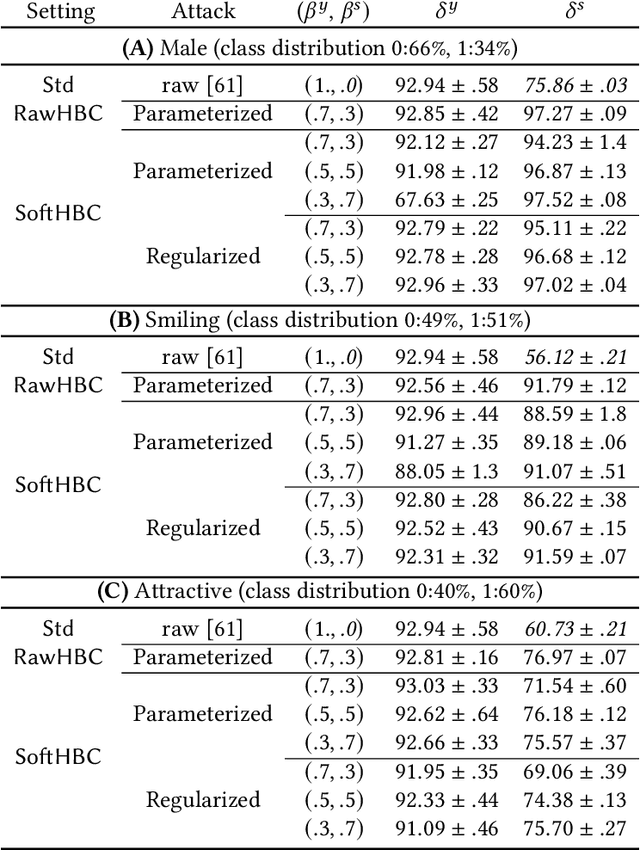
Machine unlearning (MU) aims to remove the influence of particular data points from the learnable parameters of a trained machine learning model. This is a crucial capability in light of data privacy requirements, trustworthiness, and safety in deployed models. MU is particularly challenging for deep neural networks (DNNs), such as convolutional nets or vision transformers, as such DNNs tend to memorize a notable portion of their training dataset. Nevertheless, the community lacks a rigorous and multifaceted study that looks into the success of MU methods for DNNs. In this paper, we investigate 18 state-of-the-art MU methods across various benchmark datasets and models, with each evaluation conducted over 10 different initializations, a comprehensive evaluation involving MU over 100K models. We show that, with the proper hyperparameters, Masked Small Gradients (MSG) and Convolution Transpose (CT), consistently perform better in terms of model accuracy and run-time efficiency across different models, datasets, and initializations, assessed by population-based membership inference attacks (MIA) and per-sample unlearning likelihood ratio attacks (U-LiRA). Furthermore, our benchmark highlights the fact that comparing a MU method only with commonly used baselines, such as Gradient Ascent (GA) or Successive Random Relabeling (SRL), is inadequate, and we need better baselines like Negative Gradient Plus (NG+) with proper hyperparameter selection.

P4: Towards private, personalized, and Peer-to-Peer learning

Personalized learning is a proposed approach to address the problem of data heterogeneity in collaborative machine learning. In a decentralized setting, the two main challenges of personalization are client clustering and data privacy. In this paper, we address these challenges by developing P4 (Personalized Private Peer-to-Peer) a method that ensures that each client receives a personalized model while maintaining differential privacy guarantee of each client's local dataset during and after the training. Our approach includes the design of a lightweight algorithm to identify similar clients and group them in a private, peer-to-peer (P2P) manner. Once grouped, we develop differentially-private knowledge distillation for clients to co-train with minimal impact on accuracy. We evaluate our proposed method on three benchmark datasets (FEMNIST or Federated EMNIST, CIFAR-10 and CIFAR-100) and two different neural network architectures (Linear and CNN-based networks) across a range of privacy parameters. The results demonstrate the potential of P4, as it outperforms the state-of-the-art of differential private P2P by up to 40 percent in terms of accuracy. We also show the practicality of P4 by implementing it on resource constrained devices, and validating that it has minimal overhead, e.g., about 7 seconds to run collaborative training between two clients.

On original and latent space connectivity in deep neural networks

We study whether inputs from the same class can be connected by a continuous path, in original or latent representation space, such that all points on the path are mapped by the neural network model to the same class. Understanding how the neural network views its own input space and how the latent spaces are structured has value for explainability and robustness. We show that paths, linear or nonlinear, connecting same-class inputs exist in all cases studied.

Leave-one-out Distinguishability in Machine Learning

We introduce a new analytical framework to quantify the changes in a machine learning algorithm's output distribution following the inclusion of a few data points in its training set, a notion we define as leave-one-out distinguishability (LOOD). This problem is key to measuring data **memorization** and **information leakage** in machine learning, and the **influence** of training data points on model predictions. We illustrate how our method broadens and refines existing empirical measures of memorization and privacy risks associated with training data. We use Gaussian processes to model the randomness of machine learning algorithms, and validate LOOD with extensive empirical analysis of information leakage using membership inference attacks. Our theoretical framework enables us to investigate the causes of information leakage and where the leakage is high. For example, we analyze the influence of activation functions, on data memorization. Additionally, our method allows us to optimize queries that disclose the most significant information about the training data in the leave-one-out setting. We illustrate how optimal queries can be used for accurate **reconstruction** of training data.

Privacy Risk for anisotropic Langevin dynamics using relative entropy bounds

The privacy preserving properties of Langevin dynamics with additive isotropic noise have been extensively studied. However, the isotropic noise assumption is very restrictive: (a) when adding noise to existing learning algorithms to preserve privacy and maintain the best possible accuracy one should take into account the relative magnitude of the outputs and their correlations; (b) popular algorithms such as stochastic gradient descent (and their continuous time limits) appear to possess anisotropic covariance properties. To study the privacy risks for the anisotropic noise case, one requires general results on the relative entropy between the laws of two Stochastic Differential Equations with different drifts and diffusion coefficients. Our main contribution is to establish such a bound using stability estimates for solutions to the Fokker-Planck equations via functional inequalities. With additional assumptions, the relative entropy bound implies an $(\epsilon,\delta)$-differential privacy bound. We discuss the practical implications of our bound related to privacy risk in different contexts.Finally, the benefits of anisotropic noise are illustrated using numerical results on optimising a quadratic loss or calibrating a neural network.

Data-driven initialization of deep learning solvers for Hamilton-Jacobi-Bellman PDEs

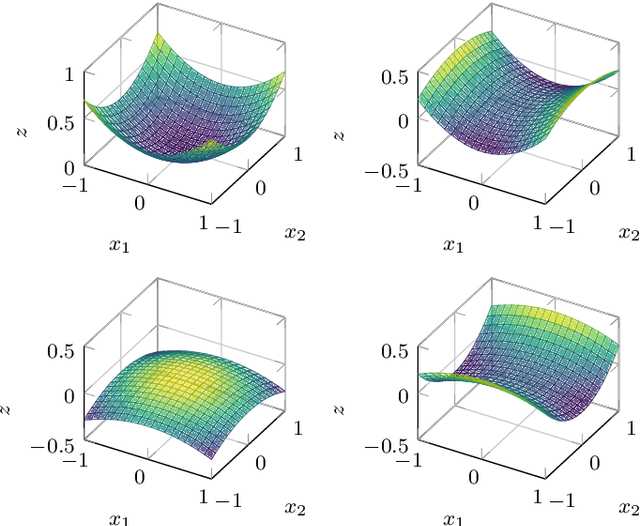
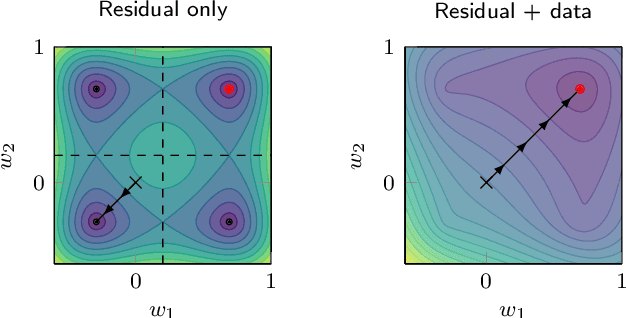
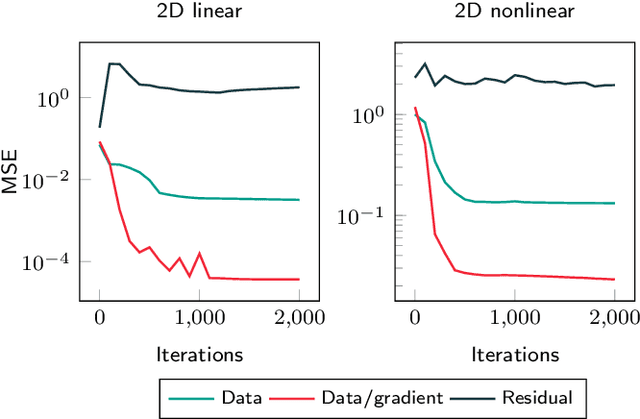
A deep learning approach for the approximation of the Hamilton-Jacobi-Bellman partial differential equation (HJB PDE) associated to the Nonlinear Quadratic Regulator (NLQR) problem. A state-dependent Riccati equation control law is first used to generate a gradient-augmented synthetic dataset for supervised learning. The resulting model becomes a warm start for the minimization of a loss function based on the residual of the HJB PDE. The combination of supervised learning and residual minimization avoids spurious solutions and mitigate the data inefficiency of a supervised learning-only approach. Numerical tests validate the different advantages of the proposed methodology.

Quantifying Information Leakage from Gradients

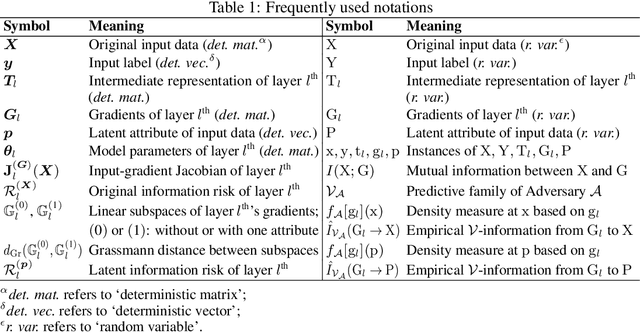
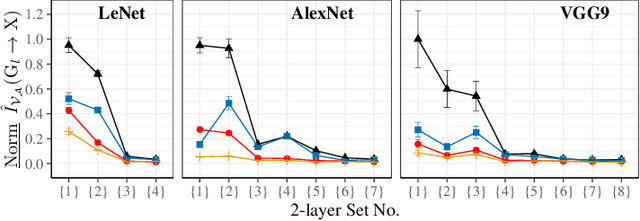
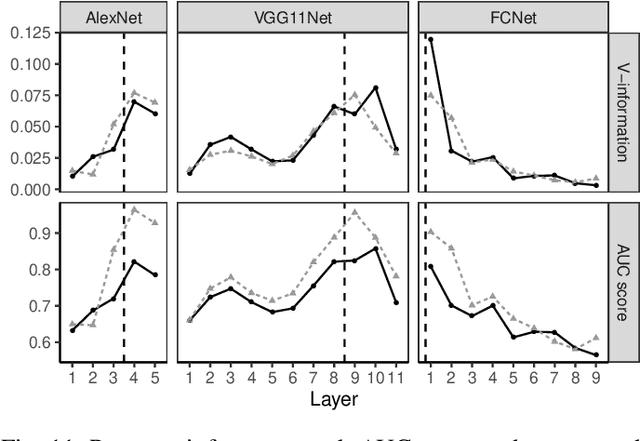
Sharing deep neural networks' gradients instead of training data could facilitate data privacy in collaborative learning. In practice however, gradients can disclose both private latent attributes and original data. Mathematical metrics are needed to quantify both original and latent information leakages from gradients computed over the training data. In this work, we first use an adaptation of the empirical $\mathcal{V}$-information to present an information-theoretic justification for the attack success rates in a layer-wise manner. We then move towards a deeper understanding of gradient leakages and propose more general and efficient metrics, using sensitivity and subspace distance to quantify the gradient changes w.r.t. original and latent information, respectively. Our empirical results, on six datasets and four models, reveal that gradients of the first layers contain the highest amount of original information, while the classifier/fully-connected layers placed after the feature extractor contain the highest latent information. Further, we show how training hyperparameters such as gradient aggregation can decrease information leakages. Our characterization provides a new understanding on gradient-based information leakages using the gradients' sensitivity w.r.t. changes in private information, and portends possible defenses such as layer-based protection or strong aggregation.

Honest-but-Curious Nets: Sensitive Attributes of Private Inputs can be Secretly Coded into the Entropy of Classifiers' Outputs

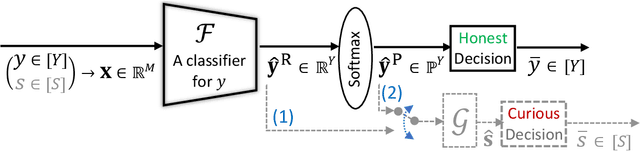
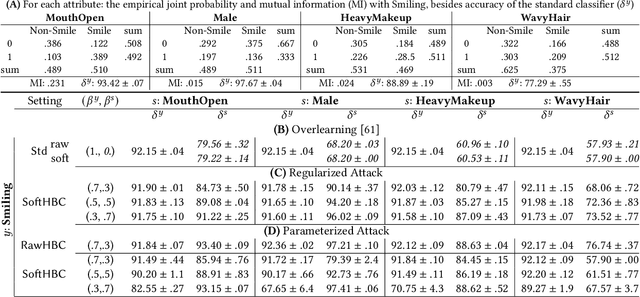
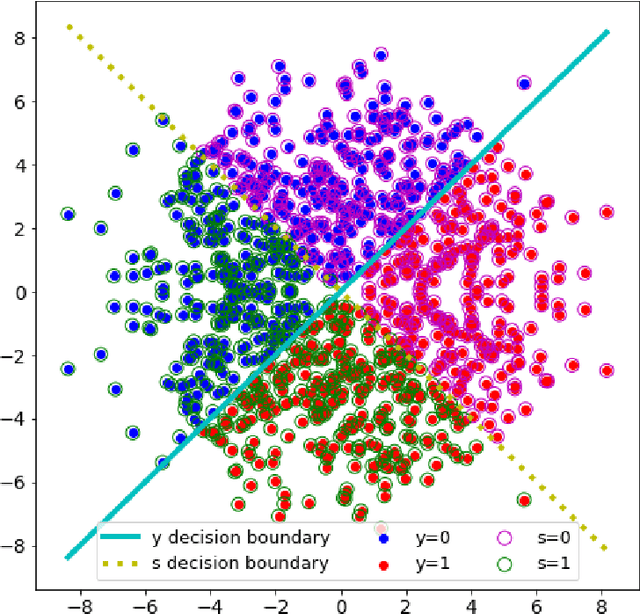
It is known that deep neural networks, trained for the classification of a non-sensitive target attribute, can reveal sensitive attributes of their input data; through features of different granularity extracted by the classifier. We, taking a step forward, show that deep classifiers can be trained to secretly encode a sensitive attribute of users' input data, at inference time, into the classifier's outputs for the target attribute. An attack that works even if users have a white-box view of the classifier, and can keep all internal representations hidden except for the classifier's estimation of the target attribute. We introduce an information-theoretical formulation of such adversaries and present efficient empirical implementations for training honest-but-curious (HBC) classifiers based on this formulation: deep models that can be accurate in predicting the target attribute, but also can utilize their outputs to secretly encode a sensitive attribute. Our evaluations on several tasks in real-world datasets show that a semi-trusted server can build a classifier that is not only perfectly honest but also accurately curious. Our work highlights a vulnerability that can be exploited by malicious machine learning service providers to attack their user's privacy in several seemingly safe scenarios; such as encrypted inferences, computations at the edge, or private knowledge distillation. We conclude by showing the difficulties in distinguishing between standard and HBC classifiers and discussing potential proactive defenses against this vulnerability of deep classifiers.

Layer-wise Characterization of Latent Information Leakage in Federated Learning

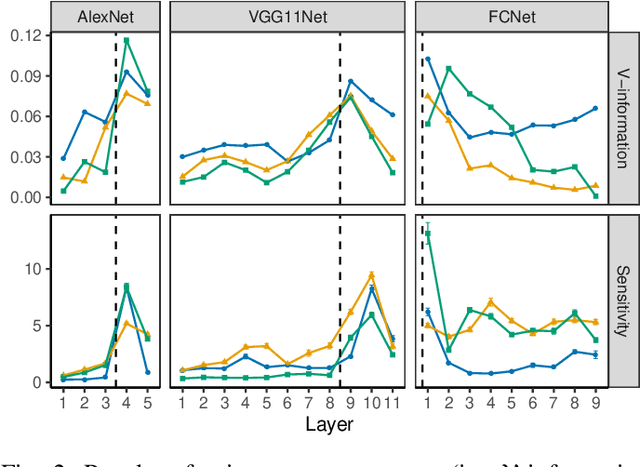
Training a deep neural network (DNN) via federated learning allows participants to share model updates (gradients), instead of the data itself. However, recent studies show that unintended latent information (e.g. gender or race) carried by the gradients can be discovered by attackers, compromising the promised privacy guarantee of federated learning. Existing privacy-preserving techniques (e.g. differential privacy) either have limited defensive capacity against the potential attacks, or suffer from considerable model utility loss. Moreover, characterizing the latent information carried by the gradients and the consequent privacy leakage has been a major theoretical and practical challenge. In this paper, we propose two new metrics to address these challenges: the empirical $\mathcal{V}$-information, a theoretically grounded notion of information which measures the amount of gradient information that is usable for an attacker, and the sensitivity analysis that utilizes the Jacobian matrix to measure the amount of changes in the gradients with respect to latent information which further quantifies private risk. We show that these metrics can localize the private information in each layer of a DNN and quantify the leakage depending on how sensitive the gradients are with respect to the latent information. As a practical application, we design LatenTZ: a federated learning framework that lets the most sensitive layers to run in the clients' Trusted Execution Environments (TEE). The implementation evaluation of LatenTZ shows that TEE-based approaches are promising for defending against powerful property inference attacks without a significant overhead in the clients' computing resources nor trading off the model's utility.

On stochastic mirror descent with interacting particles: convergence properties and variance reduction

An open problem in optimization with noisy information is the computation of an exact minimizer that is independent of the amount of noise. A standard practice in stochastic approximation algorithms is to use a decreasing step-size. However, to converge the step-size must decrease exponentially slow, and therefore this approach is not useful in practice. A second alternative is to use a fixed step-size and run independent replicas of the algorithm and average these. A third option is to run replicas of the algorithm and allow them to interact. It is unclear which of these options works best. To address this question, we reduce the problem of the computation of an exact minimizer with noisy gradient information to the study of stochastic mirror descent with interacting particles. We study the convergence of stochastic mirror descent and make explicit the tradeoffs between communication and variance reduction. We provide theoretical and numerical evidence to suggest that interaction helps to improve convergence and reduce the variance of the estimate.