Quantifying Information Leakage from Gradients

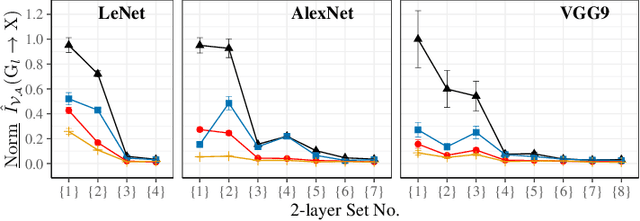
Sharing deep neural networks' gradients instead of training data could facilitate data privacy in collaborative learning. In practice however, gradients can disclose both private latent attributes and original data. Mathematical metrics are needed to quantify both original and latent information leakages from gradients computed over the training data. In this work, we first use an adaptation of the empirical $\mathcal{V}$-information to present an information-theoretic justification for the attack success rates in a layer-wise manner. We then move towards a deeper understanding of gradient leakages and propose more general and efficient metrics, using sensitivity and subspace distance to quantify the gradient changes w.r.t. original and latent information, respectively. Our empirical results, on six datasets and four models, reveal that gradients of the first layers contain the highest amount of original information, while the classifier/fully-connected layers placed after the feature extractor contain the highest latent information. Further, we show how training hyperparameters such as gradient aggregation can decrease information leakages. Our characterization provides a new understanding on gradient-based information leakages using the gradients' sensitivity w.r.t. changes in private information, and portends possible defenses such as layer-based protection or strong aggregation.