Data-driven initialization of deep learning solvers for Hamilton-Jacobi-Bellman PDEs

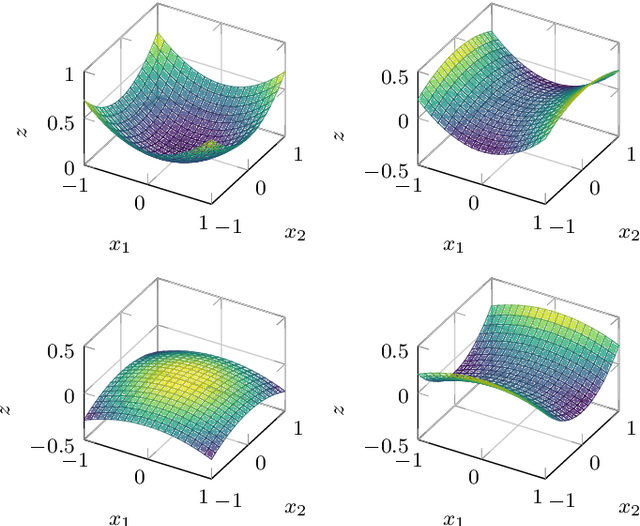
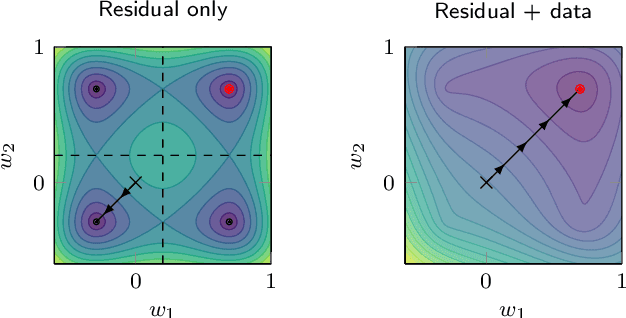
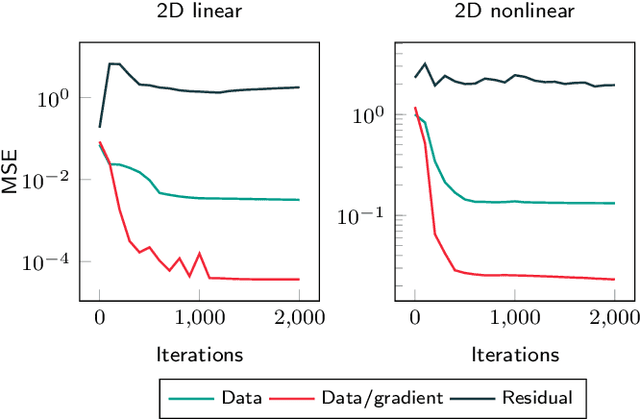
A deep learning approach for the approximation of the Hamilton-Jacobi-Bellman partial differential equation (HJB PDE) associated to the Nonlinear Quadratic Regulator (NLQR) problem. A state-dependent Riccati equation control law is first used to generate a gradient-augmented synthetic dataset for supervised learning. The resulting model becomes a warm start for the minimization of a loss function based on the residual of the HJB PDE. The combination of supervised learning and residual minimization avoids spurious solutions and mitigate the data inefficiency of a supervised learning-only approach. Numerical tests validate the different advantages of the proposed methodology.

Towards Robust and Stable Deep Learning Algorithms for Forward Backward Stochastic Differential Equations

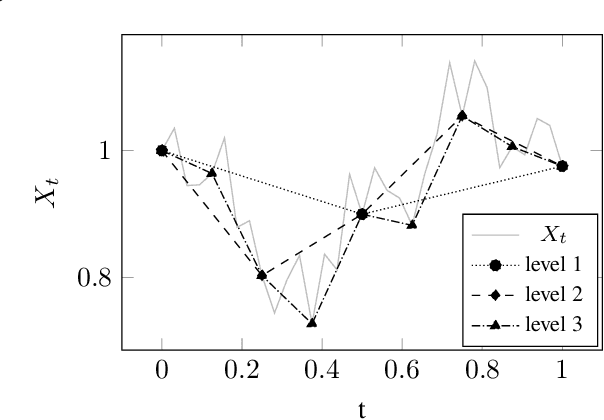
Applications in quantitative finance such as optimal trade execution, risk management of options, and optimal asset allocation involve the solution of high dimensional and nonlinear Partial Differential Equations (PDEs). The connection between PDEs and systems of Forward-Backward Stochastic Differential Equations (FBSDEs) enables the use of advanced simulation techniques to be applied even in the high dimensional setting. Unfortunately, when the underlying application contains nonlinear terms, then classical methods both for simulation and numerical methods for PDEs suffer from the curse of dimensionality. Inspired by the success of deep learning, several researchers have recently proposed to address the solution of FBSDEs using deep learning. We discuss the dynamical systems point of view of deep learning and compare several architectures in terms of stability, generalization, and robustness. In order to speed up the computations, we propose to use a multilevel discretization technique. Our preliminary results suggest that the multilevel discretization method improves solutions times by an order of magnitude compared to existing methods without sacrificing stability or robustness.

Combination of multiple Deep Learning architectures for Offensive Language Detection in Tweets

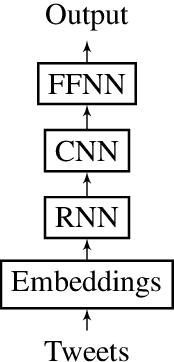
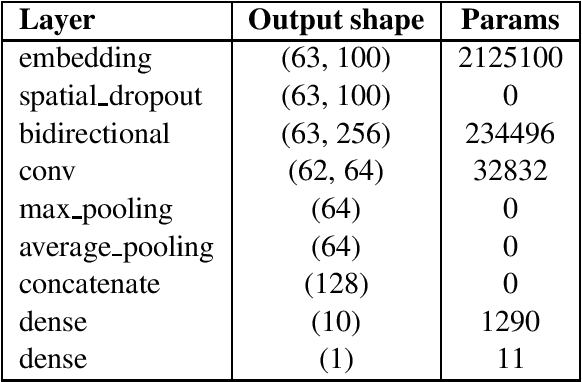
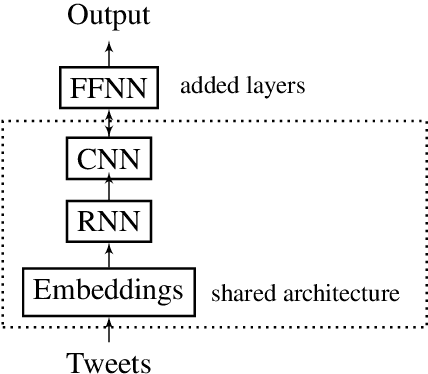
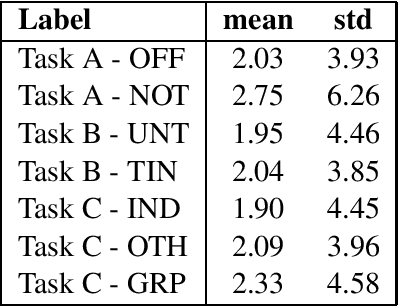
This report contains the details regarding our submission to the OffensEval 2019 (SemEval 2019 - Task 6). The competition was based on the Offensive Language Identification Dataset. We first discuss the details of the classifier implemented and the type of input data used and pre-processing performed. We then move onto critically evaluating our performance. We have achieved a macro-average F1-score of 0.76, 0.68, 0.54, respectively for Task a, Task b, and Task c, which we believe reflects on the level of sophistication of the models implemented. Finally, we will be discussing the difficulties encountered and possible improvements for the future.