Data/moment-driven approaches for fast predictive control of collective dynamics

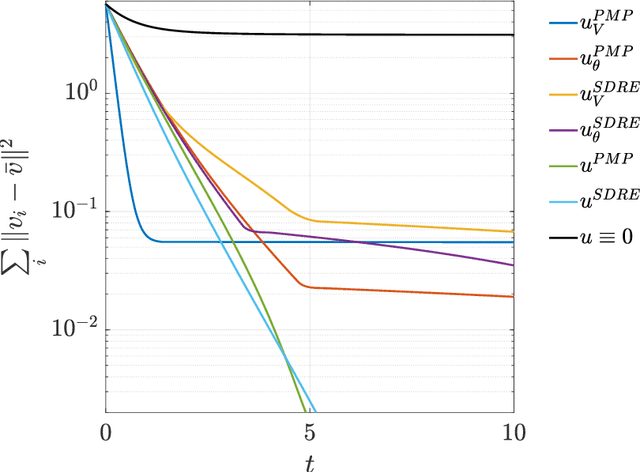
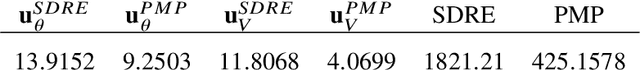
Feedback control synthesis for large-scale particle systems is reviewed in the framework of model predictive control (MPC). The high-dimensional character of collective dynamics hampers the performance of traditional MPC algorithms based on fast online dynamic optimization at every time step. Two alternatives to MPC are proposed. First, the use of supervised learning techniques for the offline approximation of optimal feedback laws is discussed. Then, a procedure based on sequential linearization of the dynamics based on macroscopic quantities of the particle ensemble is reviewed. Both approaches circumvent the online solution of optimal control problems enabling fast, real-time, feedback synthesis for large-scale particle systems. Numerical experiments assess the performance of the proposed algorithms.

Multi-level Optimal Control with Neural Surrogate Models

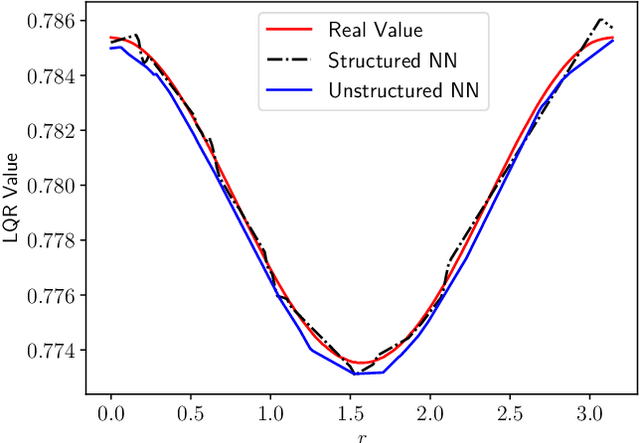
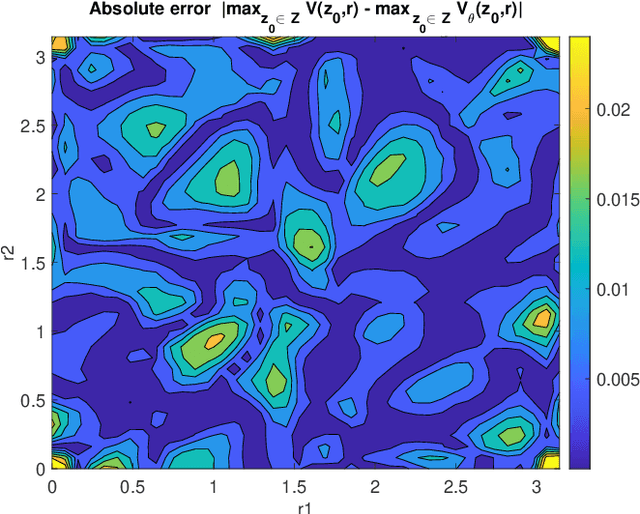
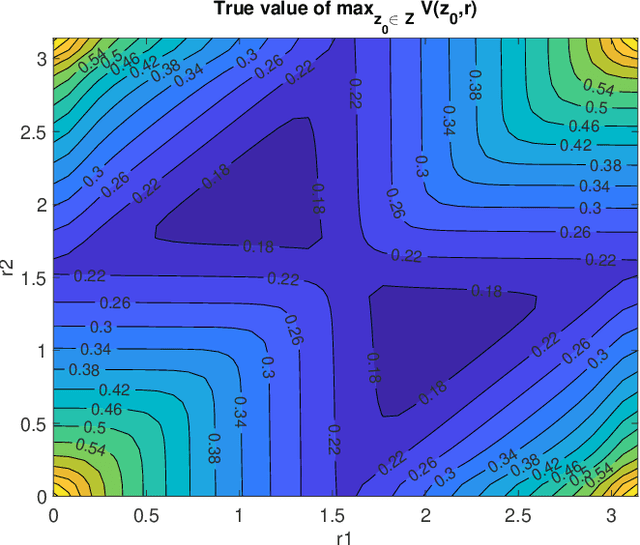
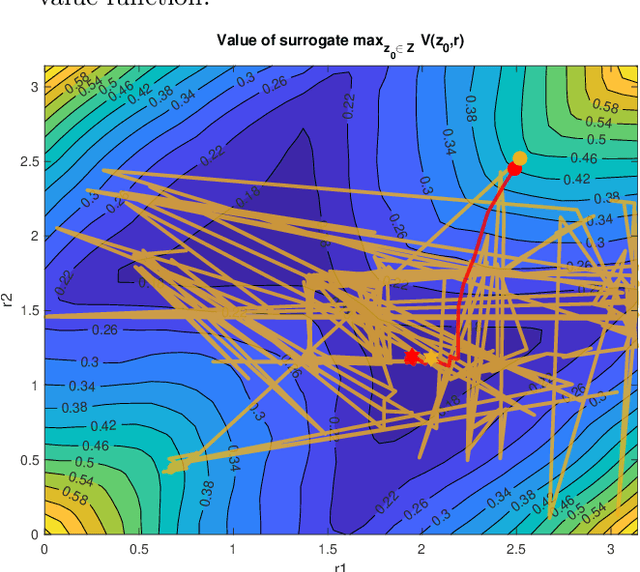
Optimal actuator and control design is studied as a multi-level optimisation problem, where the actuator design is evaluated based on the performance of the associated optimal closed loop. The evaluation of the optimal closed loop for a given actuator realisation is a computationally demanding task, for which the use of a neural network surrogate is proposed. The use of neural network surrogates to replace the lower level of the optimisation hierarchy enables the use of fast gradient-based and gradient-free consensus-based optimisation methods to determine the optimal actuator design. The effectiveness of the proposed surrogate models and optimisation methods is assessed in a test related to optimal actuator location for heat control.

Data-driven initialization of deep learning solvers for Hamilton-Jacobi-Bellman PDEs

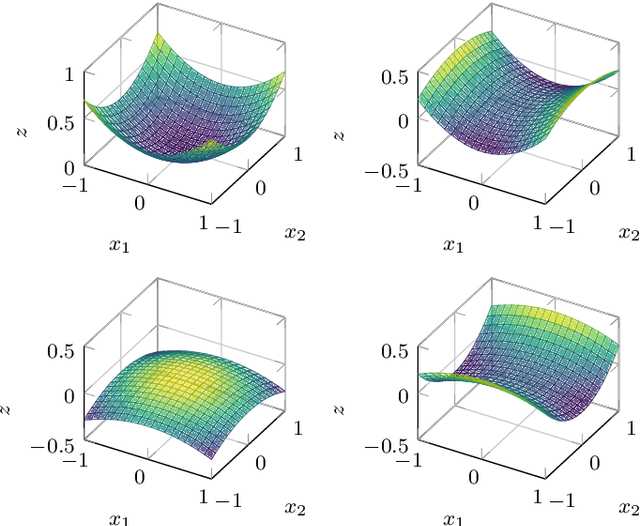
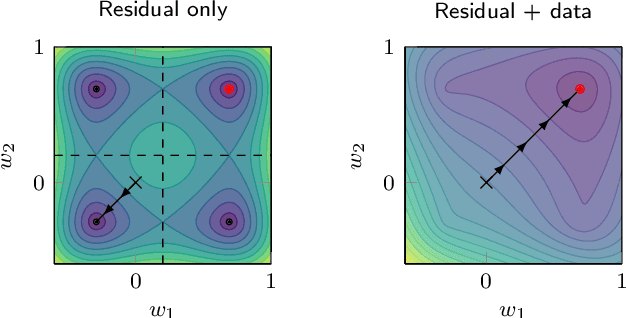
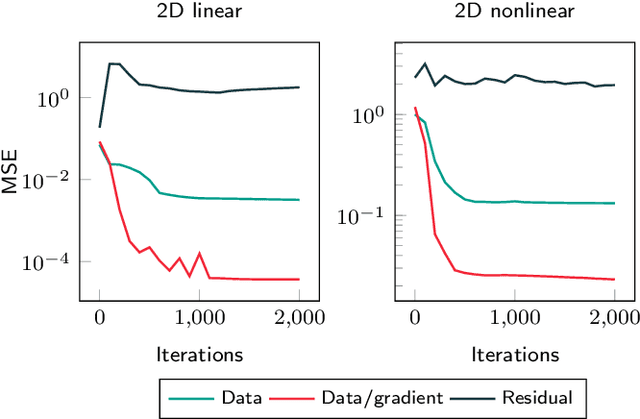
A deep learning approach for the approximation of the Hamilton-Jacobi-Bellman partial differential equation (HJB PDE) associated to the Nonlinear Quadratic Regulator (NLQR) problem. A state-dependent Riccati equation control law is first used to generate a gradient-augmented synthetic dataset for supervised learning. The resulting model becomes a warm start for the minimization of a loss function based on the residual of the HJB PDE. The combination of supervised learning and residual minimization avoids spurious solutions and mitigate the data inefficiency of a supervised learning-only approach. Numerical tests validate the different advantages of the proposed methodology.

Gradient-augmented Supervised Learning of Optimal Feedback Laws Using State-dependent Riccati Equations

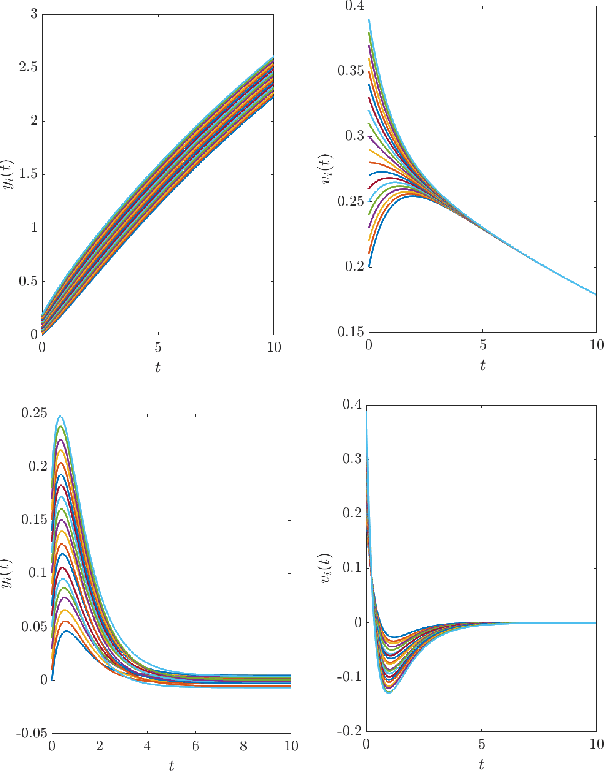
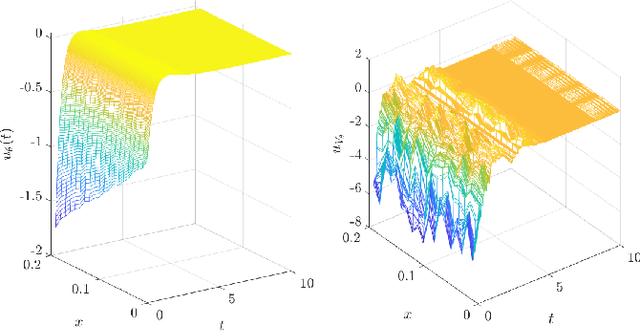
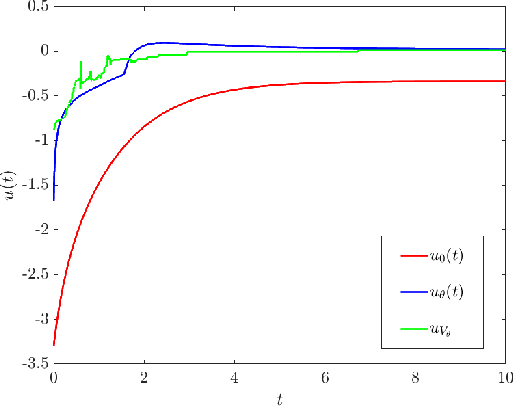
A supervised learning approach for the solution of large-scale nonlinear stabilization problems is presented. A stabilizing feedback law is trained from a dataset generated from State-dependent Riccati Equation solves. The training phase is enriched by the use gradient information in the loss function, which is weighted through the use of hyperparameters. High-dimensional nonlinear stabilization tests demonstrate that real-time sequential large-scale Algebraic Riccati Equation solves can be substituted by a suitably trained feedforward neural network.