Unified Enhancement of Privacy Bounds for Mixture Mechanisms via $f$-Differential Privacy

Differentially private (DP) machine learning algorithms incur many sources of randomness, such as random initialization, random batch subsampling, and shuffling. However, such randomness is difficult to take into account when proving differential privacy bounds because it induces mixture distributions for the algorithm's output that are difficult to analyze. This paper focuses on improving privacy bounds for shuffling models and one-iteration differentially private gradient descent (DP-GD) with random initializations using $f$-DP. We derive a closed-form expression of the trade-off function for shuffling models that outperforms the most up-to-date results based on $(\epsilon,\delta)$-DP. Moreover, we investigate the effects of random initialization on the privacy of one-iteration DP-GD. Our numerical computations of the trade-off function indicate that random initialization can enhance the privacy of DP-GD. Our analysis of $f$-DP guarantees for these mixture mechanisms relies on an inequality for trade-off functions introduced in this paper. This inequality implies the joint convexity of $F$-divergences. Finally, we study an $f$-DP analog of the advanced joint convexity of the hockey-stick divergence related to $(\epsilon,\delta)$-DP and apply it to analyze the privacy of mixture mechanisms.

Initialization Matters: Privacy-Utility Analysis of Overparameterized Neural Networks

We analytically investigate how over-parameterization of models in randomized machine learning algorithms impacts the information leakage about their training data. Specifically, we prove a privacy bound for the KL divergence between model distributions on worst-case neighboring datasets, and explore its dependence on the initialization, width, and depth of fully connected neural networks. We find that this KL privacy bound is largely determined by the expected squared gradient norm relative to model parameters during training. Notably, for the special setting of linearized network, our analysis indicates that the squared gradient norm (and therefore the escalation of privacy loss) is tied directly to the per-layer variance of the initialization distribution. By using this analysis, we demonstrate that privacy bound improves with increasing depth under certain initializations (LeCun and Xavier), while degrades with increasing depth under other initializations (He and NTK). Our work reveals a complex interplay between privacy and depth that depends on the chosen initialization distribution. We further prove excess empirical risk bounds under a fixed KL privacy budget, and show that the interplay between privacy utility trade-off and depth is similarly affected by the initialization.

Leave-one-out Distinguishability in Machine Learning

We introduce a new analytical framework to quantify the changes in a machine learning algorithm's output distribution following the inclusion of a few data points in its training set, a notion we define as leave-one-out distinguishability (LOOD). This problem is key to measuring data **memorization** and **information leakage** in machine learning, and the **influence** of training data points on model predictions. We illustrate how our method broadens and refines existing empirical measures of memorization and privacy risks associated with training data. We use Gaussian processes to model the randomness of machine learning algorithms, and validate LOOD with extensive empirical analysis of information leakage using membership inference attacks. Our theoretical framework enables us to investigate the causes of information leakage and where the leakage is high. For example, we analyze the influence of activation functions, on data memorization. Additionally, our method allows us to optimize queries that disclose the most significant information about the training data in the leave-one-out setting. We illustrate how optimal queries can be used for accurate **reconstruction** of training data.

Share Your Representation Only: Guaranteed Improvement of the Privacy-Utility Tradeoff in Federated Learning

Repeated parameter sharing in federated learning causes significant information leakage about private data, thus defeating its main purpose: data privacy. Mitigating the risk of this information leakage, using state of the art differentially private algorithms, also does not come for free. Randomized mechanisms can prevent convergence of models on learning even the useful representation functions, especially if there is more disagreement between local models on the classification functions (due to data heterogeneity). In this paper, we consider a representation federated learning objective that encourages various parties to collaboratively refine the consensus part of the model, with differential privacy guarantees, while separately allowing sufficient freedom for local personalization (without releasing it). We prove that in the linear representation setting, while the objective is non-convex, our proposed new algorithm \DPFEDREP\ converges to a ball centered around the \emph{global optimal} solution at a linear rate, and the radius of the ball is proportional to the reciprocal of the privacy budget. With this novel utility analysis, we improve the SOTA utility-privacy trade-off for this problem by a factor of $\sqrt{d}$, where $d$ is the input dimension. We empirically evaluate our method with the image classification task on CIFAR10, CIFAR100, and EMNIST, and observe a significant performance improvement over the prior work under the same small privacy budget. The code can be found in this link: https://github.com/shenzebang/CENTAUR-Privacy-Federated-Representation-Learning.

Differentially Private Learning Needs Hidden State (Or Much Faster Convergence)

Differential privacy analysis of randomized learning algorithms typically relies on composition theorems, where the implicit assumption is that the internal state of the iterative algorithm is revealed to the adversary. However, by assuming hidden states for DP algorithms (when only the last-iterate is observable), recent works prove a converging privacy bound for noisy gradient descent (on strongly convex smooth loss function) that is significantly smaller than composition bounds after $O(1/\text{step-size})$ epochs. In this paper, we extend this hidden-state analysis to the noisy mini-batch stochastic gradient descent algorithms on strongly-convex smooth loss functions. We prove converging R\'enyi DP bounds under various mini-batch sampling schemes, such as "shuffle and partition" (which are used in practical implementations of DP-SGD) and "sampling without replacement". We prove that, in these settings, our privacy bound is much smaller than the composition bound for training with a large number of iterations (which is the case for learning from high-dimensional data). Our converging privacy analysis, thus, shows that differentially private learning, with a tight bound, needs hidden state privacy analysis or a fast convergence. To complement our theoretical results, we run experiment on training classification models on MNIST, FMNIST and CIFAR-10 datasets, and observe a better accuracy given fixed privacy budgets, under the hidden-state analysis.

Enhanced Membership Inference Attacks against Machine Learning Models

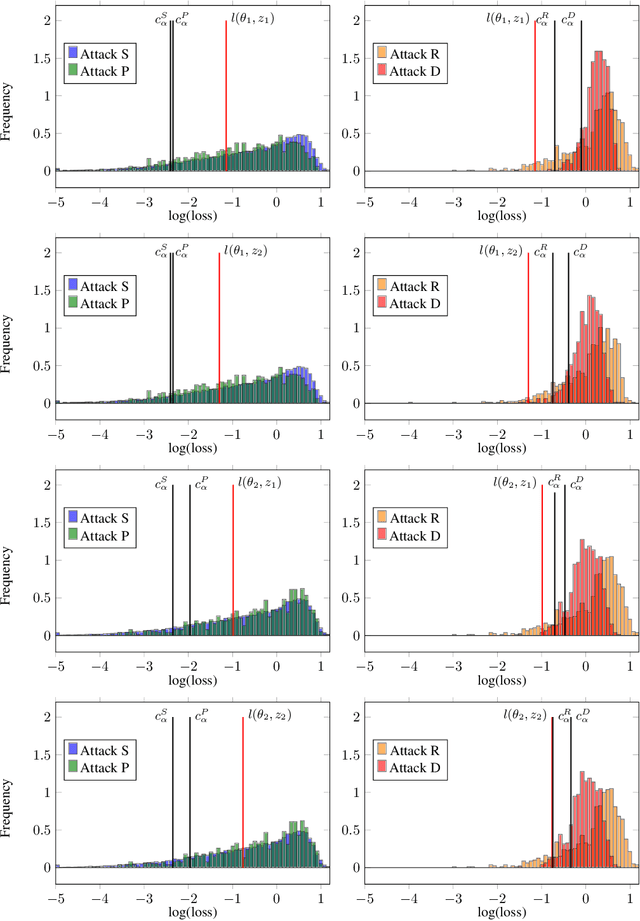
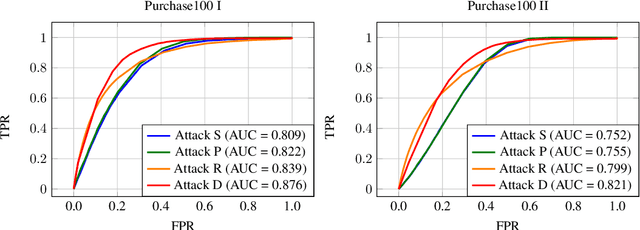
How much does a given trained model leak about each individual data record in its training set? Membership inference attacks are used as an auditing tool to quantify the private information that a model leaks about the individual data points in its training set. Membership inference attacks are influenced by different uncertainties that an attacker has to resolve about training data, the training algorithm, and the underlying data distribution. Thus attack success rates, of many attacks in the literature, do not precisely capture the information leakage of models about their data, as they also reflect other uncertainties that the attack algorithm has. In this paper, we explain the implicit assumptions and also the simplifications made in prior work using the framework of hypothesis testing. We also derive new attack algorithms from the framework that can achieve a high AUC score while also highlighting the different factors that affect their performance. Our algorithms capture a very precise approximation of privacy loss in models, and can be used as a tool to perform an accurate and informed estimation of privacy risk in machine learning models. We provide a thorough empirical evaluation of our attack strategies on various machine learning tasks and benchmark datasets.

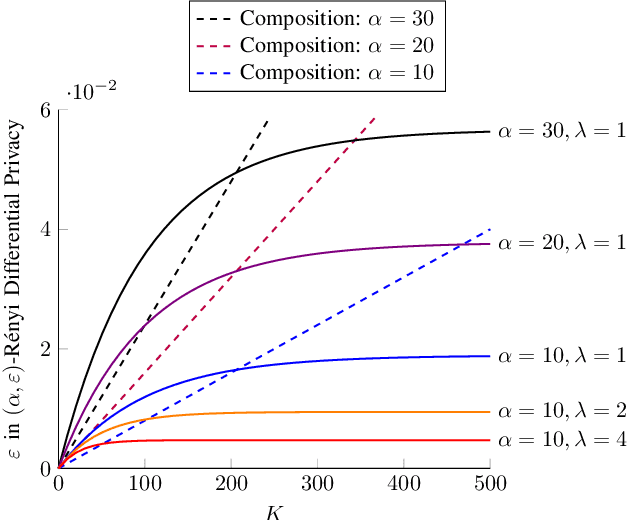
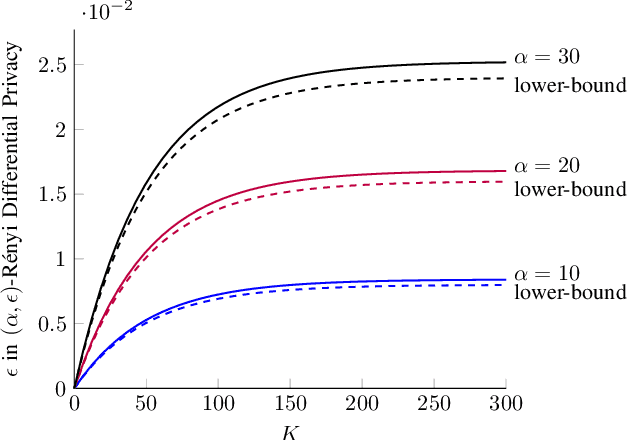
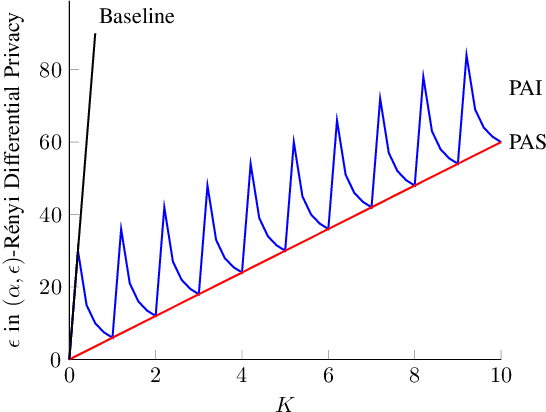
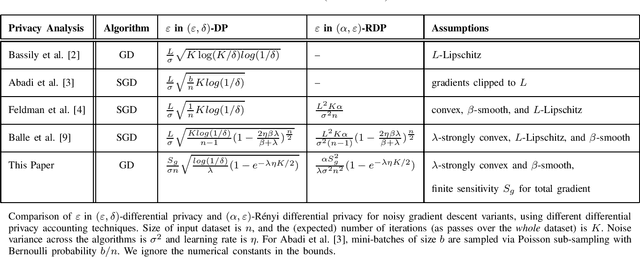
Differential Privacy Dynamics of Langevin Diffusion and Noisy Gradient Descent

We model the dynamics of privacy loss in Langevin diffusion and extend it to the noisy gradient descent algorithm: we compute a tight bound on R\'enyi differential privacy and the rate of its change throughout the learning process. We prove that the privacy loss converges exponentially fast. This significantly improves the prior privacy analysis of differentially private (stochastic) gradient descent algorithms, where (R\'enyi) privacy loss constantly increases over the training iterations. Unlike composition-based methods in differential privacy, our privacy analysis does not assume that the noisy gradients (or parameters) during the training could be revealed to the adversary. Our analysis tracks the dynamics of privacy loss through the algorithm's intermediate parameter distributions, thus allowing us to account for privacy amplification due to convergence. We prove that our privacy analysis is tight, and also provide a utility analysis for strongly convex, smooth and Lipshitz loss functions.