Differential Privacy Dynamics of Langevin Diffusion and Noisy Gradient Descent

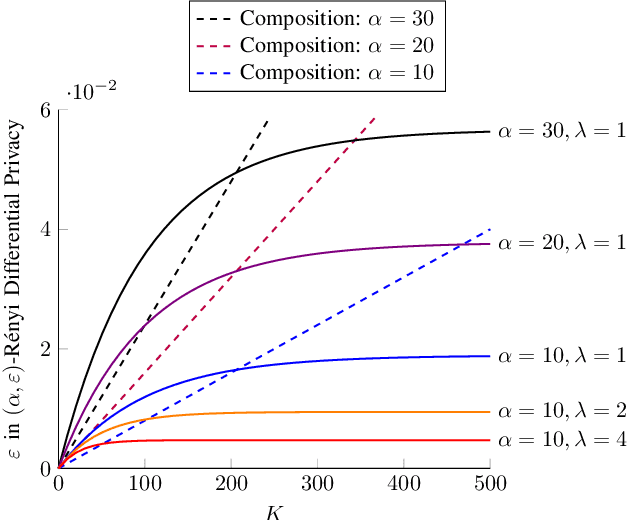
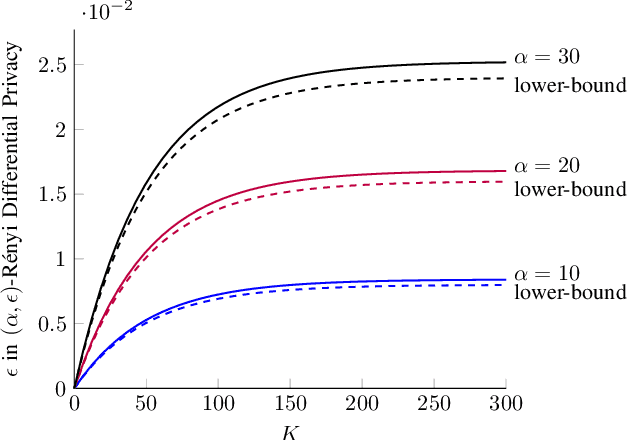
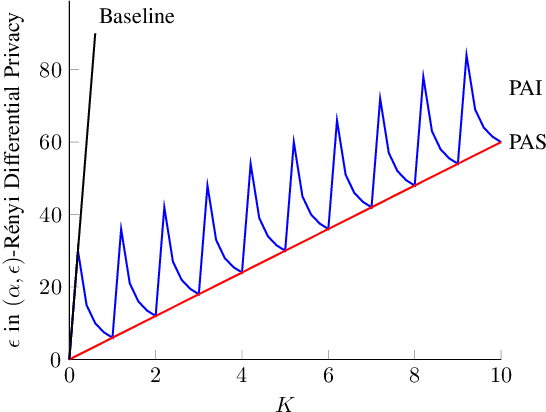
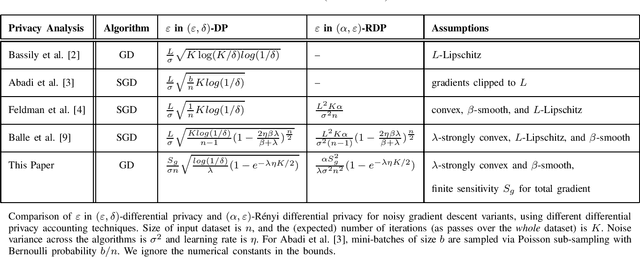
We model the dynamics of privacy loss in Langevin diffusion and extend it to the noisy gradient descent algorithm: we compute a tight bound on R\'enyi differential privacy and the rate of its change throughout the learning process. We prove that the privacy loss converges exponentially fast. This significantly improves the prior privacy analysis of differentially private (stochastic) gradient descent algorithms, where (R\'enyi) privacy loss constantly increases over the training iterations. Unlike composition-based methods in differential privacy, our privacy analysis does not assume that the noisy gradients (or parameters) during the training could be revealed to the adversary. Our analysis tracks the dynamics of privacy loss through the algorithm's intermediate parameter distributions, thus allowing us to account for privacy amplification due to convergence. We prove that our privacy analysis is tight, and also provide a utility analysis for strongly convex, smooth and Lipshitz loss functions.