Laplace Transform Interpretation of Differential Privacy

We introduce a set of useful expressions of Differential Privacy (DP) notions in terms of the Laplace transform of the privacy loss distribution. Its bare form expression appears in several related works on analyzing DP, either as an integral or an expectation. We show that recognizing the expression as a Laplace transform unlocks a new way to reason about DP properties by exploiting the duality between time and frequency domains. Leveraging our interpretation, we connect the $(q, \rho(q))$-R\'enyi DP curve and the $(\epsilon, \delta(\epsilon))$-DP curve as being the Laplace and inverse-Laplace transforms of one another. This connection shows that the R\'enyi divergence is well-defined for complex orders $q = \gamma + i \omega$. Using our Laplace transform-based analysis, we also prove an adaptive composition theorem for $(\epsilon, \delta)$-DP guarantees that is exactly tight (i.e., matches even in constants) for all values of $\epsilon$. Additionally, we resolve an issue regarding symmetry of $f$-DP on subsampling that prevented equivalence across all functional DP notions.

Forget Unlearning: Towards True Data-Deletion in Machine Learning

Unlearning has emerged as a technique to efficiently erase information of deleted records from learned models. We show, however, that the influence created by the original presence of a data point in the training set can still be detected after running certified unlearning algorithms (which can result in its reconstruction by an adversary). Thus, under realistic assumptions about the dynamics of model releases over time and in the presence of adaptive adversaries, we show that unlearning is not equivalent to data deletion and does not guarantee the "right to be forgotten." We then propose a more robust data-deletion guarantee and show that it is necessary to satisfy differential privacy to ensure true data deletion. Under our notion, we propose an accurate, computationally efficient, and secure data-deletion machine learning algorithm in the online setting based on noisy gradient descent algorithm.

Knowledge Cross-Distillation for Membership Privacy

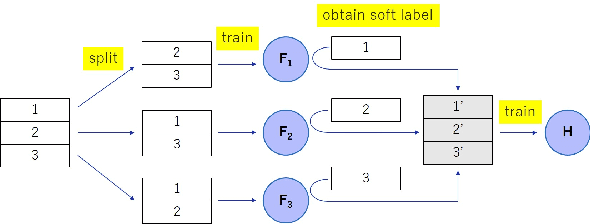
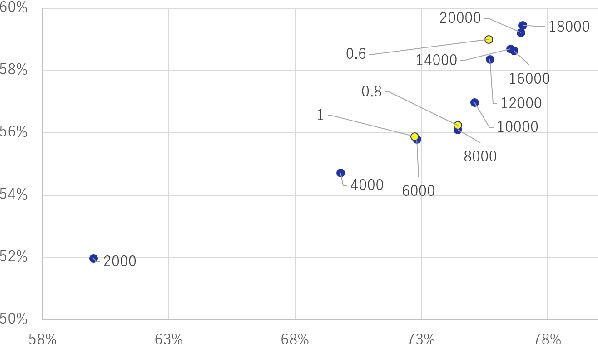
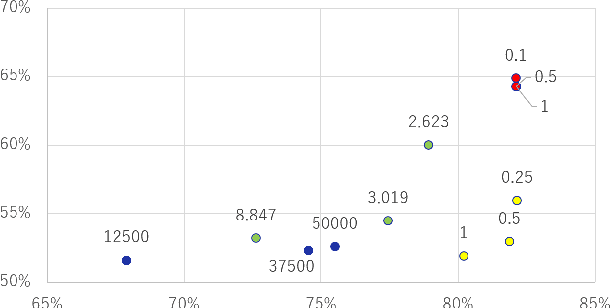
A membership inference attack (MIA) poses privacy risks on the training data of a machine learning model. With an MIA, an attacker guesses if the target data are a member of the training dataset. The state-of-the-art defense against MIAs, distillation for membership privacy (DMP), requires not only private data to protect but a large amount of unlabeled public data. However, in certain privacy-sensitive domains, such as medical and financial, the availability of public data is not obvious. Moreover, a trivial method to generate the public data by using generative adversarial networks significantly decreases the model accuracy, as reported by the authors of DMP. To overcome this problem, we propose a novel defense against MIAs using knowledge distillation without requiring public data. Our experiments show that the privacy protection and accuracy of our defense are comparable with those of DMP for the benchmark tabular datasets used in MIA researches, Purchase100 and Texas100, and our defense has much better privacy-utility trade-off than those of the existing defenses without using public data for image dataset CIFAR10.

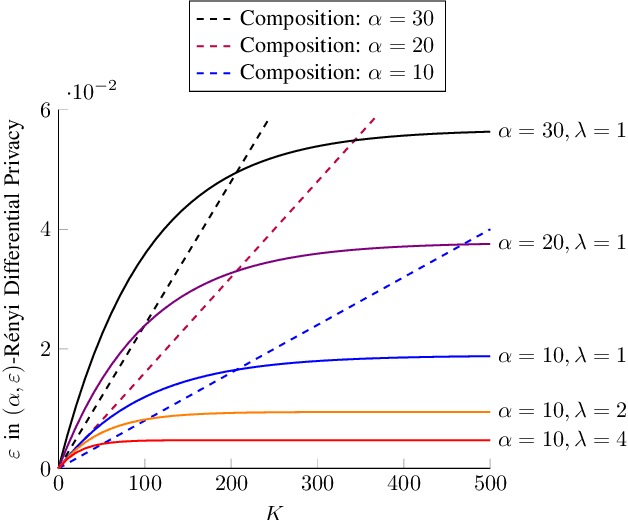
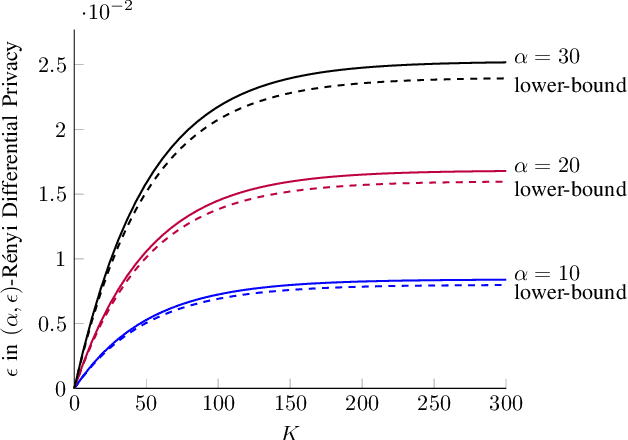
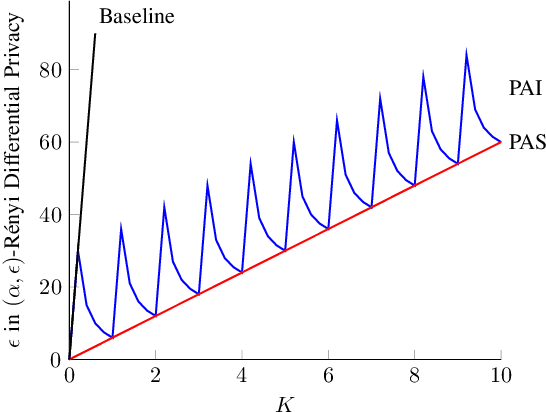
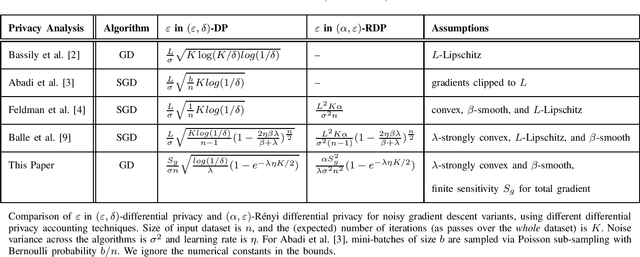
Differential Privacy Dynamics of Langevin Diffusion and Noisy Gradient Descent

We model the dynamics of privacy loss in Langevin diffusion and extend it to the noisy gradient descent algorithm: we compute a tight bound on R\'enyi differential privacy and the rate of its change throughout the learning process. We prove that the privacy loss converges exponentially fast. This significantly improves the prior privacy analysis of differentially private (stochastic) gradient descent algorithms, where (R\'enyi) privacy loss constantly increases over the training iterations. Unlike composition-based methods in differential privacy, our privacy analysis does not assume that the noisy gradients (or parameters) during the training could be revealed to the adversary. Our analysis tracks the dynamics of privacy loss through the algorithm's intermediate parameter distributions, thus allowing us to account for privacy amplification due to convergence. We prove that our privacy analysis is tight, and also provide a utility analysis for strongly convex, smooth and Lipshitz loss functions.

Unifying Ensemble Methods for Q-learning via Social Choice Theory

Ensemble methods have been widely applied in Reinforcement Learning (RL) in order to enhance stability, increase convergence speed, and improve exploration. These methods typically work by employing an aggregation mechanism over actions of different RL algorithms. We show that a variety of these methods can be unified by drawing parallels from committee voting rules in Social Choice Theory. We map the problem of designing an action aggregation mechanism in an ensemble method to a voting problem which, under different voting rules, yield popular ensemble-based RL algorithms like Majority Voting Q-learning or Bootstrapped Q-learning. Our unification framework, in turn, allows us to design new ensemble-RL algorithms with better performance. For instance, we map two diversity-centered committee voting rules, namely Single Non-Transferable Voting Rule and Chamberlin-Courant Rule, into new RL algorithms that demonstrate excellent exploratory behavior in our experiments.