LREF: A Novel LLM-based Relevance Framework for E-commerce

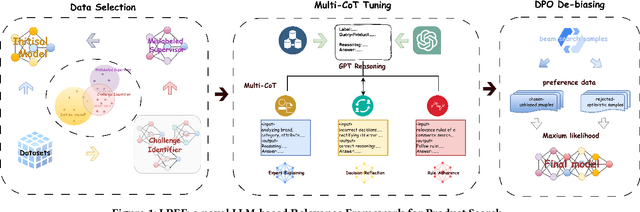
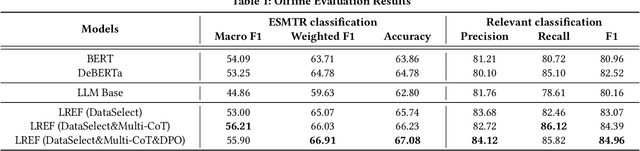
Query and product relevance prediction is a critical component for ensuring a smooth user experience in e-commerce search. Traditional studies mainly focus on BERT-based models to assess the semantic relevance between queries and products. However, the discriminative paradigm and limited knowledge capacity of these approaches restrict their ability to comprehend the relevance between queries and products fully. With the rapid advancement of Large Language Models (LLMs), recent research has begun to explore their application to industrial search systems, as LLMs provide extensive world knowledge and flexible optimization for reasoning processes. Nonetheless, directly leveraging LLMs for relevance prediction tasks introduces new challenges, including a high demand for data quality, the necessity for meticulous optimization of reasoning processes, and an optimistic bias that can result in over-recall. To overcome the above problems, this paper proposes a novel framework called the LLM-based RElevance Framework (LREF) aimed at enhancing e-commerce search relevance. The framework comprises three main stages: supervised fine-tuning (SFT) with Data Selection, Multiple Chain of Thought (Multi-CoT) tuning, and Direct Preference Optimization (DPO) for de-biasing. We evaluate the performance of the framework through a series of offline experiments on large-scale real-world datasets, as well as online A/B testing. The results indicate significant improvements in both offline and online metrics. Ultimately, the model was deployed in a well-known e-commerce application, yielding substantial commercial benefits.

Multi-Step Alignment as Markov Games: An Optimistic Online Gradient Descent Approach with Convergence Guarantees

Reinforcement Learning from Human Feedback (RLHF) has been highly successful in aligning large language models with human preferences. While prevalent methods like DPO have demonstrated strong performance, they frame interactions with the language model as a bandit problem, which limits their applicability in real-world scenarios where multi-turn conversations are common. Additionally, DPO relies on the Bradley-Terry model assumption, which does not adequately capture the non-transitive nature of human preferences. In this paper, we address these challenges by modeling the alignment problem as a two-player constant-sum Markov game, where each player seeks to maximize their winning rate against the other across all steps of the conversation. Our approach Multi-step Preference Optimization (MPO) is built upon the natural actor-critic framework~\citep{peters2008natural}. We further develop OMPO based on the optimistic online gradient descent algorithm~\citep{rakhlin2013online,joulani17a}. Theoretically, we provide a rigorous analysis for both algorithms on convergence and show that OMPO requires $\mathcal{O}(\epsilon^{-1})$ policy updates to converge to an $\epsilon$-approximate Nash equilibrium. We also validate the effectiveness of our method on multi-turn conversations dataset and math reasoning dataset.

Training Deep Learning Models with Norm-Constrained LMOs

In this work, we study optimization methods that leverage the linear minimization oracle (LMO) over a norm-ball. We propose a new stochastic family of algorithms that uses the LMO to adapt to the geometry of the problem and, perhaps surprisingly, show that they can be applied to unconstrained problems. The resulting update rule unifies several existing optimization methods under a single framework. Furthermore, we propose an explicit choice of norm for deep architectures, which, as a side benefit, leads to the transferability of hyperparameters across model sizes. Experimentally, we demonstrate significant speedups on nanoGPT training without any reliance on Adam. The proposed method is memory-efficient, requiring only one set of model weights and one set of gradients, which can be stored in half-precision.

Initialization Matters: Privacy-Utility Analysis of Overparameterized Neural Networks

We analytically investigate how over-parameterization of models in randomized machine learning algorithms impacts the information leakage about their training data. Specifically, we prove a privacy bound for the KL divergence between model distributions on worst-case neighboring datasets, and explore its dependence on the initialization, width, and depth of fully connected neural networks. We find that this KL privacy bound is largely determined by the expected squared gradient norm relative to model parameters during training. Notably, for the special setting of linearized network, our analysis indicates that the squared gradient norm (and therefore the escalation of privacy loss) is tied directly to the per-layer variance of the initialization distribution. By using this analysis, we demonstrate that privacy bound improves with increasing depth under certain initializations (LeCun and Xavier), while degrades with increasing depth under other initializations (He and NTK). Our work reveals a complex interplay between privacy and depth that depends on the chosen initialization distribution. We further prove excess empirical risk bounds under a fixed KL privacy budget, and show that the interplay between privacy utility trade-off and depth is similarly affected by the initialization.

Sample Complexity Bounds for Score-Matching: Causal Discovery and Generative Modeling

This paper provides statistical sample complexity bounds for score-matching and its applications in causal discovery. We demonstrate that accurate estimation of the score function is achievable by training a standard deep ReLU neural network using stochastic gradient descent. We establish bounds on the error rate of recovering causal relationships using the score-matching-based causal discovery method of Rolland et al. [2022], assuming a sufficiently good estimation of the score function. Finally, we analyze the upper bound of score-matching estimation within the score-based generative modeling, which has been applied for causal discovery but is also of independent interest within the domain of generative models.

Benign Overfitting in Deep Neural Networks under Lazy Training

This paper focuses on over-parameterized deep neural networks (DNNs) with ReLU activation functions and proves that when the data distribution is well-separated, DNNs can achieve Bayes-optimal test error for classification while obtaining (nearly) zero-training error under the lazy training regime. For this purpose, we unify three interrelated concepts of overparameterization, benign overfitting, and the Lipschitz constant of DNNs. Our results indicate that interpolating with smoother functions leads to better generalization. Furthermore, we investigate the special case where interpolating smooth ground-truth functions is performed by DNNs under the Neural Tangent Kernel (NTK) regime for generalization. Our result demonstrates that the generalization error converges to a constant order that only depends on label noise and initialization noise, which theoretically verifies benign overfitting. Our analysis provides a tight lower bound on the normalized margin under non-smooth activation functions, as well as the minimum eigenvalue of NTK under high-dimensional settings, which has its own interest in learning theory.

Extrapolation and Spectral Bias of Neural Nets with Hadamard Product: a Polynomial Net Study

Neural tangent kernel (NTK) is a powerful tool to analyze training dynamics of neural networks and their generalization bounds. The study on NTK has been devoted to typical neural network architectures, but is incomplete for neural networks with Hadamard products (NNs-Hp), e.g., StyleGAN and polynomial neural networks. In this work, we derive the finite-width NTK formulation for a special class of NNs-Hp, i.e., polynomial neural networks. We prove their equivalence to the kernel regression predictor with the associated NTK, which expands the application scope of NTK. Based on our results, we elucidate the separation of PNNs over standard neural networks with respect to extrapolation and spectral bias. Our two key insights are that when compared to standard neural networks, PNNs are able to fit more complicated functions in the extrapolation regime and admit a slower eigenvalue decay of the respective NTK. Besides, our theoretical results can be extended to other types of NNs-Hp, which expand the scope of our work. Our empirical results validate the separations in broader classes of NNs-Hp, which provide a good justification for a deeper understanding of neural architectures.

Robustness in deep learning: The good , the bad , and the ugly

We study the average robustness notion in deep neural networks in (selected) wide and narrow, deep and shallow, as well as lazy and non-lazy training settings. We prove that in the under-parameterized setting, width has a negative effect while it improves robustness in the over-parameterized setting. The effect of depth closely depends on the initialization and the training mode. In particular, when initialized with LeCun initialization, depth helps robustness with lazy training regime. In contrast, when initialized with Neural Tangent Kernel (NTK) and He-initialization, depth hurts the robustness. Moreover, under non-lazy training regime, we demonstrate how the width of a two-layer ReLU network benefits robustness. Our theoretical developments improve the results by Huang et al. [2021], Wu et al. [2021] and are consistent with Bubeck and Sellke [2021], Bubeck et al. [2021].

Generalization Properties of NAS under Activation and Skip Connection Search

Neural Architecture Search (NAS) has fostered the automatic discovery of neural architectures, which achieve state-of-the-art accuracy in image recognition. Despite the progress achieved with NAS, so far there is little attention to theoretical guarantees on NAS. In this work, we study the generalization properties of NAS under a unifying framework enabling (deep) layer skip connection search and activation function search. To this end, we derive the lower (and upper) bounds of the minimum eigenvalue of Neural Tangent Kernel under the (in)finite width regime from a search space including mixed activation functions, fully connected, and residual neural networks. Our analysis is non-trivial due to the coupling of various architectures and activation functions under the unifying framework. Then, we leverage the eigenvalue bounds to establish generalization error bounds of NAS in the stochastic gradient descent training. Importantly, we theoretically and experimentally show how the derived results can guide NAS to select the top-performing architectures, even in the case without training, leading to a training-free algorithm based on our theory. Accordingly, our numerical validation shed light on the design of computationally efficient methods for NAS.

Controlling the Complexity and Lipschitz Constant improves polynomial nets

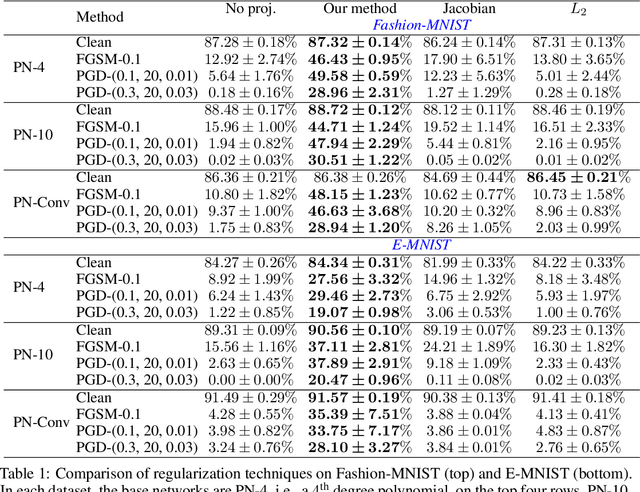
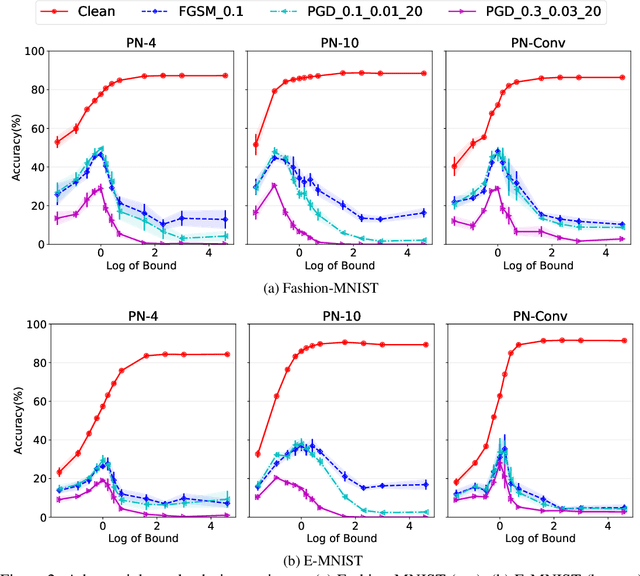
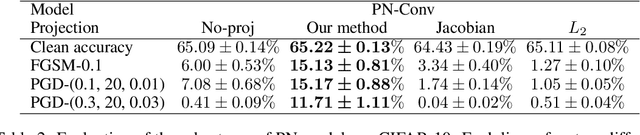
While the class of Polynomial Nets demonstrates comparable performance to neural networks (NN), it currently has neither theoretical generalization characterization nor robustness guarantees. To this end, we derive new complexity bounds for the set of Coupled CP-Decomposition (CCP) and Nested Coupled CP-decomposition (NCP) models of Polynomial Nets in terms of the $\ell_\infty$-operator-norm and the $\ell_2$-operator norm. In addition, we derive bounds on the Lipschitz constant for both models to establish a theoretical certificate for their robustness. The theoretical results enable us to propose a principled regularization scheme that we also evaluate experimentally in six datasets and show that it improves the accuracy as well as the robustness of the models to adversarial perturbations. We showcase how this regularization can be combined with adversarial training, resulting in further improvements.