MaD-Mix: Multi-Modal Data Mixtures via Latent Space Coupling for Vision-Language Model Training

Vision-Language Models (VLMs) are typically trained on a diverse set of multi-modal domains, yet current practices rely on costly manual tuning. We propose MaD-Mix, a principled and computationally efficient framework that derives multi-modal data mixtures for VLM training. MaD-Mix formulates data mixing as modality-aware domain alignment maximization and obtains closed-form multi-modal alignment scores from the Fenchel dual through inter-modal coupling variables. MaD-Mix systematically handles domains with missing modalities, allowing for the integration of language-only domains. Empirical evaluations across 0.5B and 7B models demonstrate that MaD-Mix accelerates VLM training across diverse benchmarks. MaD-Mix matches human-tuned data mixtures using 22% fewer training steps in image-text instruction tuning. In complex tri-modal video-image-text scenarios, where manual tuning becomes impractical, MaD-Mix boosts average accuracy over uniform weights, with negligible mixture computation overhead (< 1 GPU-hour), enabling scalable mixture design for modern VLM pipelines.

Chameleon: A Flexible Data-mixing Framework for Language Model Pretraining and Finetuning

Training data mixtures greatly impact the generalization performance of large language models. Existing domain reweighting methods often rely on costly weight computations and require retraining when new data is introduced. To this end, we introduce a flexible and efficient data mixing framework, Chameleon, that employs leverage scores to quantify domain importance within a learned embedding space. We first construct a domain affinity matrix over domain embeddings. The induced leverage scores determine a mixture that upweights domains sharing common representations in embedding space. This formulation allows direct transfer to new data by computing the new domain embeddings. In experiments, we demonstrate improvements over three key scenarios: (i) our computed weights improve performance on pretraining domains with a fraction of the compute of existing methods; (ii) Chameleon can adapt to data changes without proxy retraining, boosting few-shot reasoning accuracies when transferred to new data; (iii) our method enables efficient domain reweighting in finetuning, consistently improving test perplexity on all finetuning domains over uniform mixture. Our code is available at https://github.com/LIONS-EPFL/Chameleon.

Training Deep Learning Models with Norm-Constrained LMOs

In this work, we study optimization methods that leverage the linear minimization oracle (LMO) over a norm-ball. We propose a new stochastic family of algorithms that uses the LMO to adapt to the geometry of the problem and, perhaps surprisingly, show that they can be applied to unconstrained problems. The resulting update rule unifies several existing optimization methods under a single framework. Furthermore, we propose an explicit choice of norm for deep architectures, which, as a side benefit, leads to the transferability of hyperparameters across model sizes. Experimentally, we demonstrate significant speedups on nanoGPT training without any reliance on Adam. The proposed method is memory-efficient, requiring only one set of model weights and one set of gradients, which can be stored in half-precision.

SAMPa: Sharpness-aware Minimization Parallelized

Sharpness-aware minimization (SAM) has been shown to improve the generalization of neural networks. However, each SAM update requires \emph{sequentially} computing two gradients, effectively doubling the per-iteration cost compared to base optimizers like SGD. We propose a simple modification of SAM, termed SAMPa, which allows us to fully parallelize the two gradient computations. SAMPa achieves a twofold speedup of SAM under the assumption that communication costs between devices are negligible. Empirical results show that SAMPa ranks among the most efficient variants of SAM in terms of computational time. Additionally, our method consistently outperforms SAM across both vision and language tasks. Notably, SAMPa theoretically maintains convergence guarantees even for \emph{fixed} perturbation sizes, which is established through a novel Lyapunov function. We in fact arrive at SAMPa by treating this convergence guarantee as a hard requirement -- an approach we believe is promising for developing SAM-based methods in general. Our code is available at \url{https://github.com/LIONS-EPFL/SAMPa}.

Improving SAM Requires Rethinking its Optimization Formulation

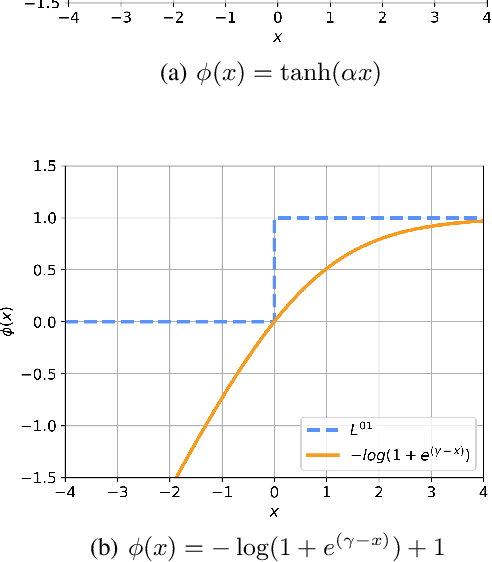
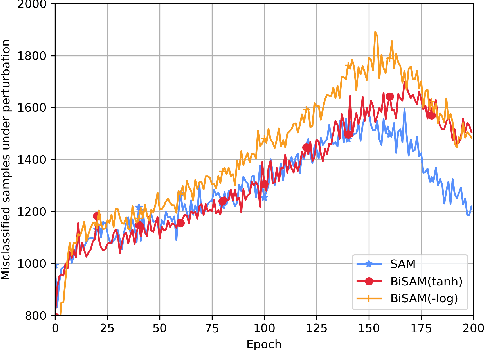
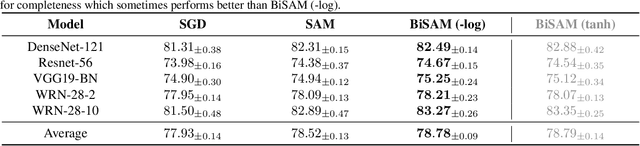
This paper rethinks Sharpness-Aware Minimization (SAM), which is originally formulated as a zero-sum game where the weights of a network and a bounded perturbation try to minimize/maximize, respectively, the same differentiable loss. To fundamentally improve this design, we argue that SAM should instead be reformulated using the 0-1 loss. As a continuous relaxation, we follow the simple conventional approach where the minimizing (maximizing) player uses an upper bound (lower bound) surrogate to the 0-1 loss. This leads to a novel formulation of SAM as a bilevel optimization problem, dubbed as BiSAM. BiSAM with newly designed lower-bound surrogate loss indeed constructs stronger perturbation. Through numerical evidence, we show that BiSAM consistently results in improved performance when compared to the original SAM and variants, while enjoying similar computational complexity. Our code is available at https://github.com/LIONS-EPFL/BiSAM.

Stable Nonconvex-Nonconcave Training via Linear Interpolation

This paper presents a theoretical analysis of linear interpolation as a principled method for stabilizing (large-scale) neural network training. We argue that instabilities in the optimization process are often caused by the nonmonotonicity of the loss landscape and show how linear interpolation can help by leveraging the theory of nonexpansive operators. We construct a new optimization scheme called relaxed approximate proximal point (RAPP), which is the first explicit method to achieve last iterate convergence rates for the full range of cohypomonotone problems. The construction extends to constrained and regularized settings. By replacing the inner optimizer in RAPP we rediscover the family of Lookahead algorithms for which we establish convergence in cohypomonotone problems even when the base optimizer is taken to be gradient descent ascent. The range of cohypomonotone problems in which Lookahead converges is further expanded by exploiting that Lookahead inherits the properties of the base optimizer. We corroborate the results with experiments on generative adversarial networks which demonstrates the benefits of the linear interpolation present in both RAPP and Lookahead.