Optimal Stopping with Gaussian Processes

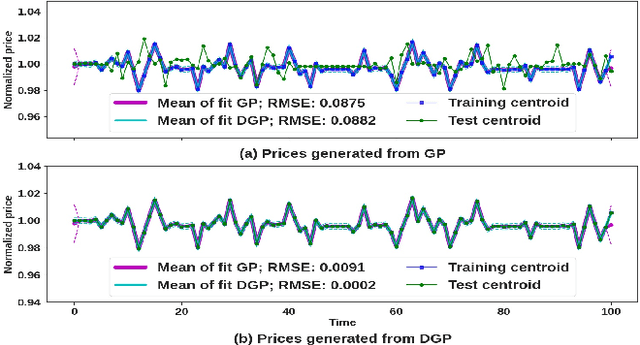
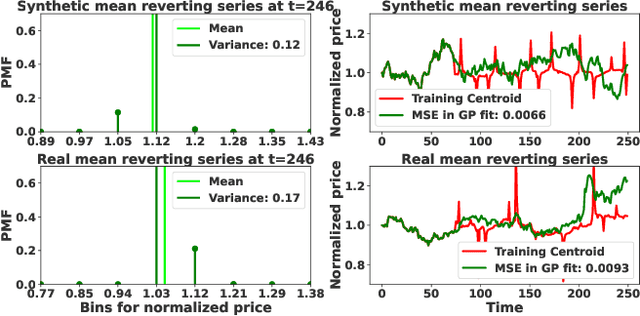
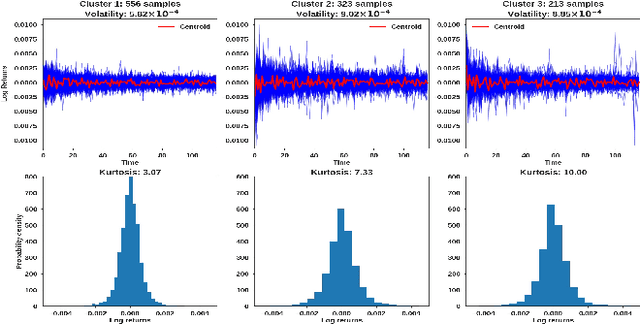
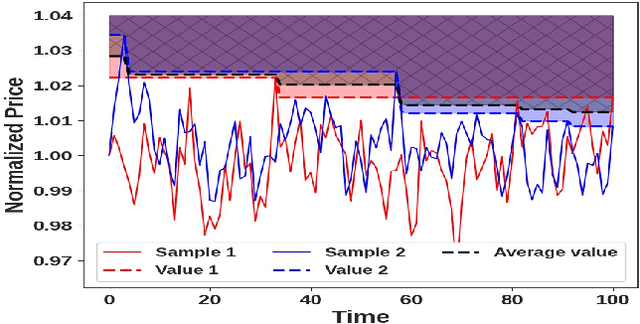
We propose a novel group of Gaussian Process based algorithms for fast approximate optimal stopping of time series with specific applications to financial markets. We show that structural properties commonly exhibited by financial time series (e.g., the tendency to mean-revert) allow the use of Gaussian and Deep Gaussian Process models that further enable us to analytically evaluate optimal stopping value functions and policies. We additionally quantify uncertainty in the value function by propagating the price model through the optimal stopping analysis. We compare and contrast our proposed methods against a sampling-based method, as well as a deep learning based benchmark that is currently considered the state-of-the-art in the literature. We show that our family of algorithms outperforms benchmarks on three historical time series datasets that include intra-day and end-of-day equity stock prices as well as the daily US treasury yield curve rates.

One-Shot Learning of Stochastic Differential Equations with Computational Graph Completion

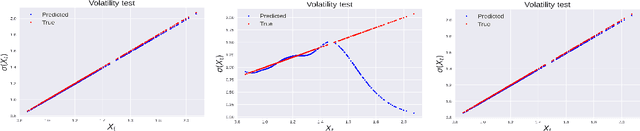
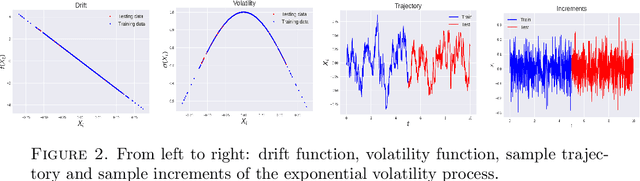
We consider the problem of learning Stochastic Differential Equations of the form $dX_t = f(X_t)dt+\sigma(X_t)dW_t $ from one sample trajectory. This problem is more challenging than learning deterministic dynamical systems because one sample trajectory only provides indirect information on the unknown functions $f$, $\sigma$, and stochastic process $dW_t$ representing the drift, the diffusion, and the stochastic forcing terms, respectively. We propose a simple kernel-based solution to this problem that can be decomposed as follows: (1) Represent the time-increment map $X_t \rightarrow X_{t+dt}$ as a Computational Graph in which $f$, $\sigma$ and $dW_t$ appear as unknown functions and random variables. (2) Complete the graph (approximate unknown functions and random variables) via Maximum a Posteriori Estimation (given the data) with Gaussian Process (GP) priors on the unknown functions. (3) Learn the covariance functions (kernels) of the GP priors from data with randomized cross-validation. Numerical experiments illustrate the efficacy, robustness, and scope of our method.

Uncertainty Quantification of the 4th kind; optimal posterior accuracy-uncertainty tradeoff with the minimum enclosing ball

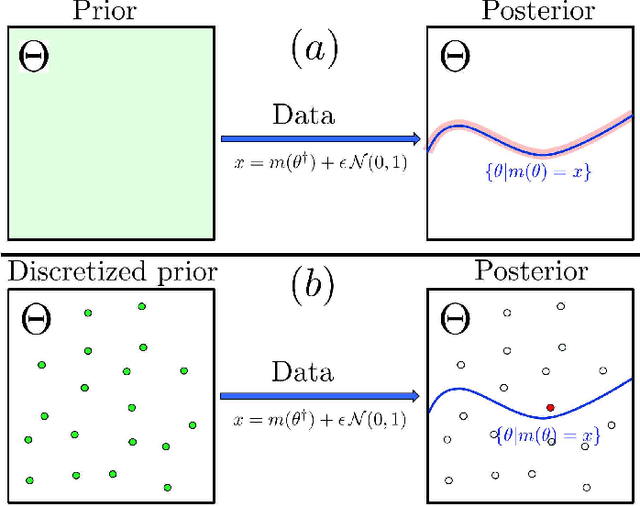
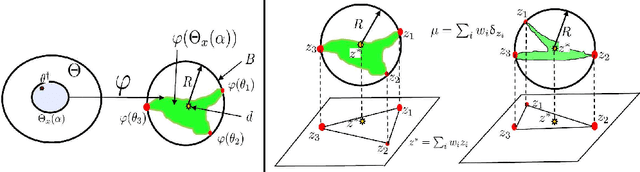
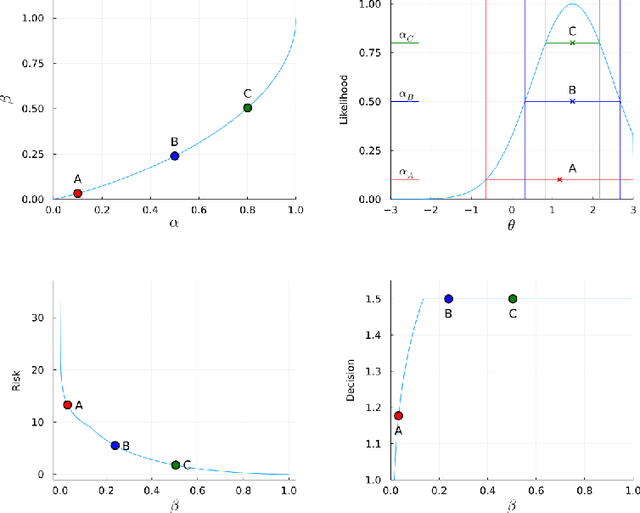
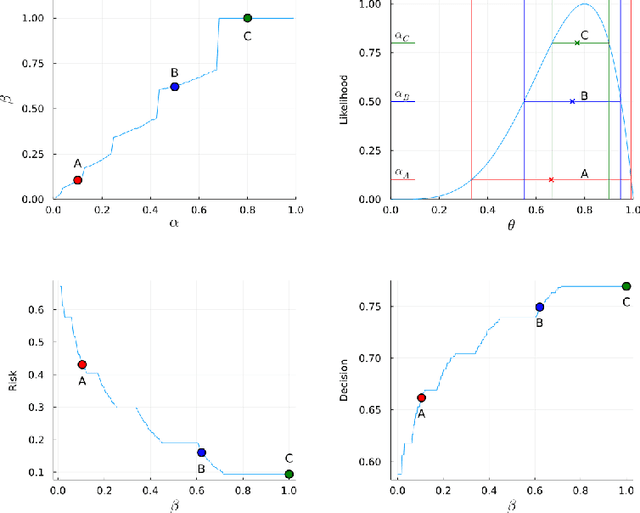
There are essentially three kinds of approaches to Uncertainty Quantification (UQ): (A) robust optimization, (B) Bayesian, (C) decision theory. Although (A) is robust, it is unfavorable with respect to accuracy and data assimilation. (B) requires a prior, it is generally brittle and posterior estimations can be slow. Although (C) leads to the identification of an optimal prior, its approximation suffers from the curse of dimensionality and the notion of risk is one that is averaged with respect to the distribution of the data. We introduce a 4th kind which is a hybrid between (A), (B), (C), and hypothesis testing. It can be summarized as, after observing a sample $x$, (1) defining a likelihood region through the relative likelihood and (2) playing a minmax game in that region to define optimal estimators and their risk. The resulting method has several desirable properties (a) an optimal prior is identified after measuring the data, and the notion of risk is a posterior one, (b) the determination of the optimal estimate and its risk can be reduced to computing the minimum enclosing ball of the image of the likelihood region under the quantity of interest map (which is fast and not subject to the curse of dimensionality). The method is characterized by a parameter in $ [0,1]$ acting as an assumed lower bound on the rarity of the observed data (the relative likelihood). When that parameter is near $1$, the method produces a posterior distribution concentrated around a maximum likelihood estimate with tight but low confidence UQ estimates. When that parameter is near $0$, the method produces a maximal risk posterior distribution with high confidence UQ estimates. In addition to navigating the accuracy-uncertainty tradeoff, the proposed method addresses the brittleness of Bayesian inference by navigating the robustness-accuracy tradeoff associated with data assimilation.

Deterministic Iteratively Built KD-Tree with KNN Search for Exact Applications

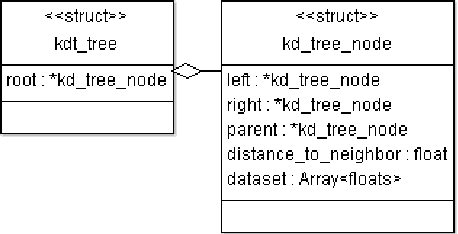
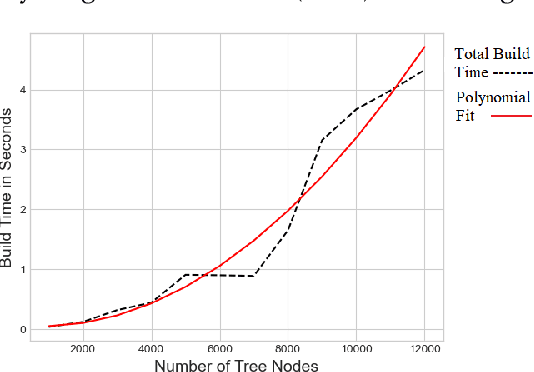
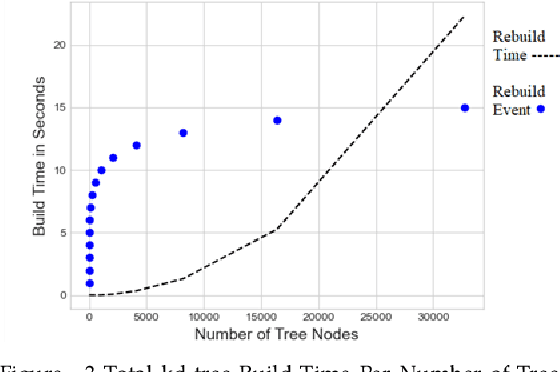
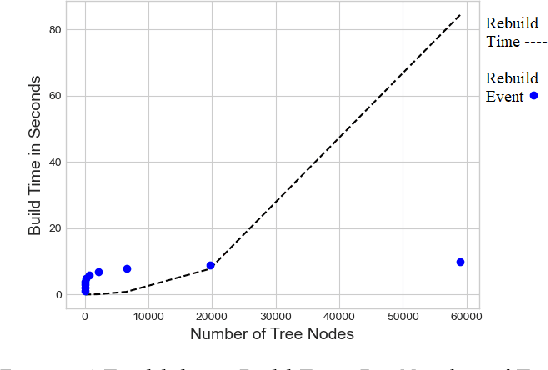
K-Nearest Neighbors (KNN) search is a fundamental algorithm in artificial intelligence software with applications in robotics, and autonomous vehicles. These wide-ranging applications utilize KNN either directly for simple classification or combine KNN results as input to other algorithms such as Locally Weighted Learning (LWL). Similar to binary trees, kd-trees become unbalanced as new data is added in online applications which can lead to rapid degradation in search performance unless the tree is rebuilt. Although approximate methods are suitable for graphics applications, which prioritize query speed over query accuracy, they are unsuitable for certain applications in autonomous systems, aeronautics, and robotic manipulation where exact solutions are desired. In this paper, we will attempt to assess the performance of non-recursive deterministic kd-tree functions and KNN functions. We will also present a "forest of interval kd-trees" which reduces the number of tree rebuilds, without compromising the exactness of query results.

Decision Theoretic Bootstrapping

The design and testing of supervised machine learning models combine two fundamental distributions: (1) the training data distribution (2) the testing data distribution. Although these two distributions are identical and identifiable when the data set is infinite; they are imperfectly known (and possibly distinct) when the data is finite (and possibly corrupted) and this uncertainty must be taken into account for robust Uncertainty Quantification (UQ). We present a general decision-theoretic bootstrapping solution to this problem: (1) partition the available data into a training subset and a UQ subset (2) take $m$ subsampled subsets of the training set and train $m$ models (3) partition the UQ set into $n$ sorted subsets and take a random fraction of them to define $n$ corresponding empirical distributions $\mu_{j}$ (4) consider the adversarial game where Player I selects a model $i\in\left\{ 1,\ldots,m\right\} $, Player II selects the UQ distribution $\mu_{j}$ and Player I receives a loss defined by evaluating the model $i$ against data points sampled from $\mu_{j}$ (5) identify optimal mixed strategies (probability distributions over models and UQ distributions) for both players. These randomized optimal mixed strategies provide optimal model mixtures and UQ estimates given the adversarial uncertainty of the training and testing distributions represented by the game. The proposed approach provides (1) some degree of robustness to distributional shift in both the distribution of training data and that of the testing data (2) conditional probability distributions on the output space forming aleatory representations of the uncertainty on the output as a function of the input variable.

Adversarial Poisoning Attacks and Defense for General Multi-Class Models Based On Synthetic Reduced Nearest Neighbors

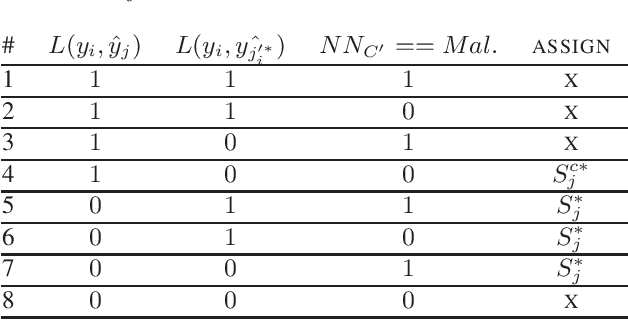
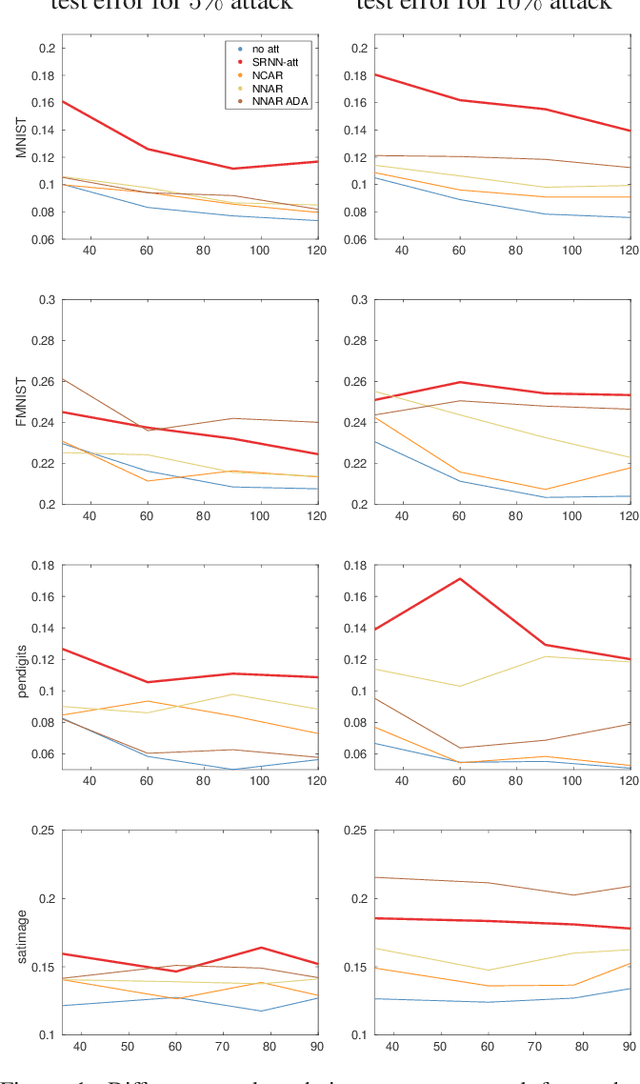
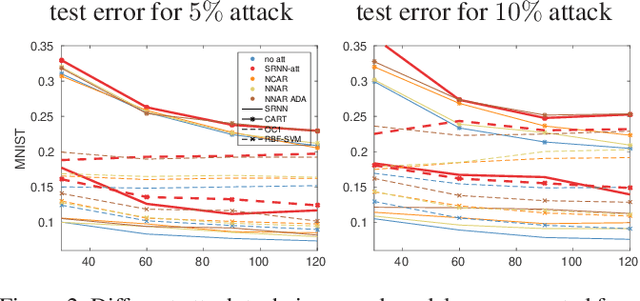
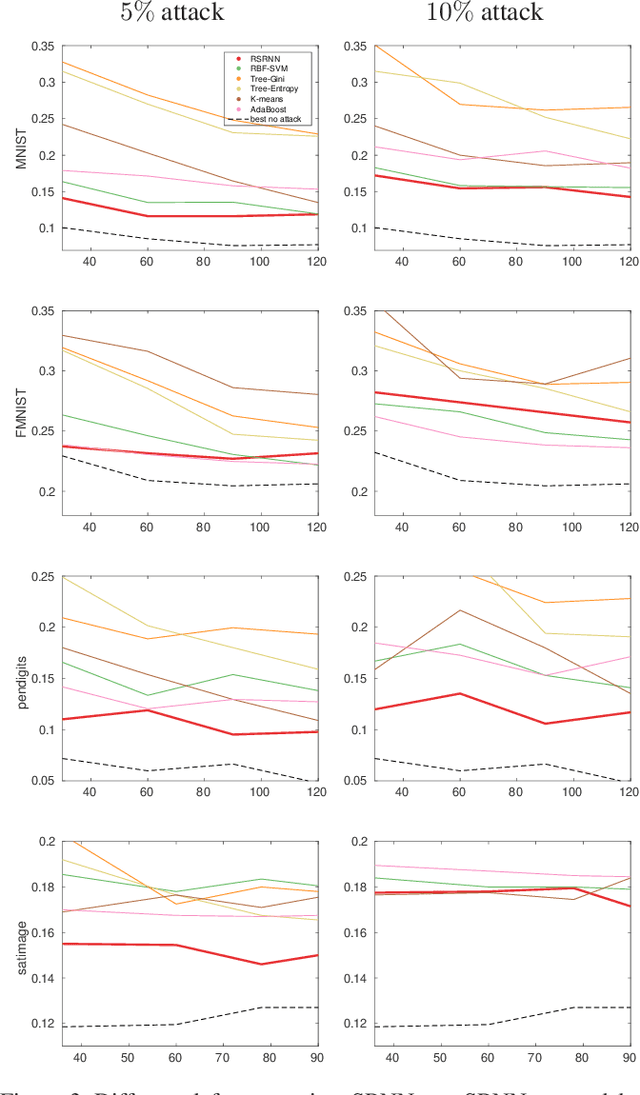
State-of-the-art machine learning models are vulnerable to data poisoning attacks whose purpose is to undermine the integrity of the model. However, the current literature on data poisoning attacks is mainly focused on ad hoc techniques that are only applicable to specific machine learning models. Additionally, the existing data poisoning attacks in the literature are limited to either binary classifiers or to gradient-based algorithms. To address these limitations, this paper first proposes a novel model-free label-flipping attack based on the multi-modality of the data, in which the adversary targets the clusters of classes while constrained by a label-flipping budget. The complexity of our proposed attack algorithm is linear in time over the size of the dataset. Also, the proposed attack can increase the error up to two times for the same attack budget. Second, a novel defense technique based on the Synthetic Reduced Nearest Neighbor (SRNN) model is proposed. The defense technique can detect and exclude flipped samples on the fly during the training procedure. Through extensive experimental analysis, we demonstrate that (i) the proposed attack technique can deteriorate the accuracy of several models drastically, and (ii) under the proposed attack, the proposed defense technique significantly outperforms other conventional machine learning models in recovering the accuracy of the targeted model.

Discrete linear-complexity reinforcement learning in continuous action spaces for Q-learning algorithms

In this article, we sketch an algorithm that extends the Q-learning algorithms to the continuous action space domain. Our method is based on the discretization of the action space. Despite the commonly used discretization methods, our method does not increase the discretized problem dimensionality exponentially. We will show that our proposed method is linear in complexity when the discretization is employed. The variant of the Q-learning algorithm presented in this work, labeled as Finite Step Q-Learning (FSQ), can be deployed to both shallow and deep neural network architectures.

Parameter Selection Algorithm For Continuous Variables

In this article, we propose a new algorithm for supervised learning methods, by which one can both capture the non-linearity in data and also find the best subset model. To produce an enhanced subset of the original variables, an ideal selection method should have the potential of adding a supplementary level of regression analysis that would capture complex relationships in the data via mathematical transformation of the predictors and exploration of synergistic effects of combined variables. The method that we present here has the potential to produce an optimal subset of variables, rendering the overall process of model selection to be more efficient. The core objective of this paper is to introduce a new estimation technique for the classical least square regression framework. This new automatic variable transformation and model selection method could offer an optimal and stable model that minimizes the mean square error and variability, while combining all possible subset selection methodology and including variable transformations and interaction. Moreover, this novel method controls multicollinearity, leading to an optimal set of explanatory variables.