ELATE: Evolutionary Language model for Automated Time-series Engineering

Time-series prediction involves forecasting future values using machine learning models. Feature engineering, whereby existing features are transformed to make new ones, is critical for enhancing model performance, but is often manual and time-intensive. Existing automation attempts rely on exhaustive enumeration, which can be computationally costly and lacks domain-specific insights. We introduce ELATE (Evolutionary Language model for Automated Time-series Engineering), which leverages a language model within an evolutionary framework to automate feature engineering for time-series data. ELATE employs time-series statistical measures and feature importance metrics to guide and prune features, while the language model proposes new, contextually relevant feature transformations. Our experiments demonstrate that ELATE improves forecasting accuracy by an average of 8.4% across various domains.

Model Evaluation in the Dark: Robust Classifier Metrics with Missing Labels

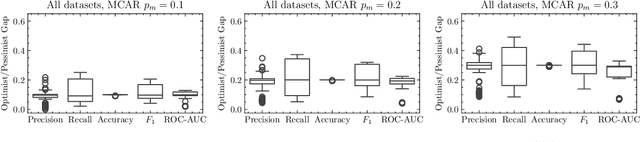
Missing data in supervised learning is well-studied, but the specific issue of missing labels during model evaluation has been overlooked. Ignoring samples with missing values, a common solution, can introduce bias, especially when data is Missing Not At Random (MNAR). We propose a multiple imputation technique for evaluating classifiers using metrics such as precision, recall, and ROC-AUC. This method not only offers point estimates but also a predictive distribution for these quantities when labels are missing. We empirically show that the predictive distribution's location and shape are generally correct, even in the MNAR regime. Moreover, we establish that this distribution is approximately Gaussian and provide finite-sample convergence bounds. Additionally, a robustness proof is presented, confirming the validity of the approximation under a realistic error model.

MAFE: Multi-Agent Fair Environments for Decision-Making Systems

Fairness constraints applied to machine learning (ML) models in static contexts have been shown to potentially produce adverse outcomes among demographic groups over time. To address this issue, emerging research focuses on creating fair solutions that persist over time. While many approaches treat this as a single-agent decision-making problem, real-world systems often consist of multiple interacting entities that influence outcomes. Explicitly modeling these entities as agents enables more flexible analysis of their interventions and the effects they have on a system's underlying dynamics. A significant challenge in conducting research on multi-agent systems is the lack of realistic environments that leverage the limited real-world data available for analysis. To address this gap, we introduce the concept of a Multi-Agent Fair Environment (MAFE) and present and analyze three MAFEs that model distinct social systems. Experimental results demonstrate the utility of our MAFEs as testbeds for developing multi-agent fair algorithms.

Are Logistic Models Really Interpretable?

The demand for open and trustworthy AI models points towards widespread publishing of model weights. Consumers of these model weights must be able to act accordingly with the information provided. That said, one of the simplest AI classification models, Logistic Regression (LR), has an unwieldy interpretation of its model weights, with greater difficulties when extending LR to generalised additive models. In this work, we show via a User Study that skilled participants are unable to reliably reproduce the action of small LR models given the trained parameters. As an antidote to this, we define Linearised Additive Models (LAMs), an optimal piecewise linear approximation that augments any trained additive model equipped with a sigmoid link function, requiring no retraining. We argue that LAMs are more interpretable than logistic models -- survey participants are shown to solve model reasoning tasks with LAMs much more accurately than with LR given the same information. Furthermore, we show that LAMs do not suffer from large performance penalties in terms of ROC-AUC and calibration with respect to their logistic counterparts on a broad suite of public financial modelling data.

Cross-Domain Graph Data Scaling: A Showcase with Diffusion Models

Models for natural language and images benefit from data scaling behavior: the more data fed into the model, the better they perform. This 'better with more' phenomenon enables the effectiveness of large-scale pre-training on vast amounts of data. However, current graph pre-training methods struggle to scale up data due to heterogeneity across graphs. To achieve effective data scaling, we aim to develop a general model that is able to capture diverse data patterns of graphs and can be utilized to adaptively help the downstream tasks. To this end, we propose UniAug, a universal graph structure augmentor built on a diffusion model. We first pre-train a discrete diffusion model on thousands of graphs across domains to learn the graph structural patterns. In the downstream phase, we provide adaptive enhancement by conducting graph structure augmentation with the help of the pre-trained diffusion model via guided generation. By leveraging the pre-trained diffusion model for structure augmentation, we consistently achieve performance improvements across various downstream tasks in a plug-and-play manner. To the best of our knowledge, this study represents the first demonstration of a data-scaling graph structure augmentor on graphs across domains.

Characterizing Multimodal Long-form Summarization: A Case Study on Financial Reports

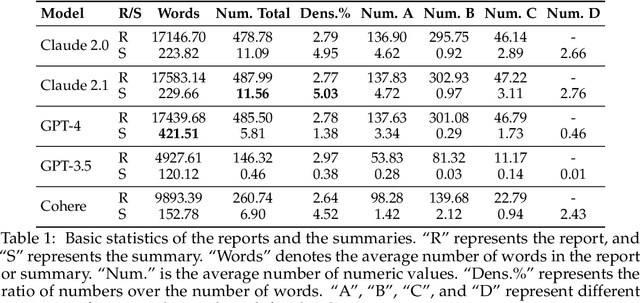
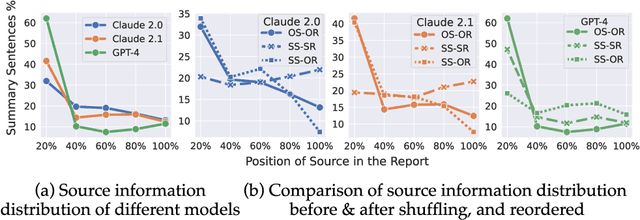
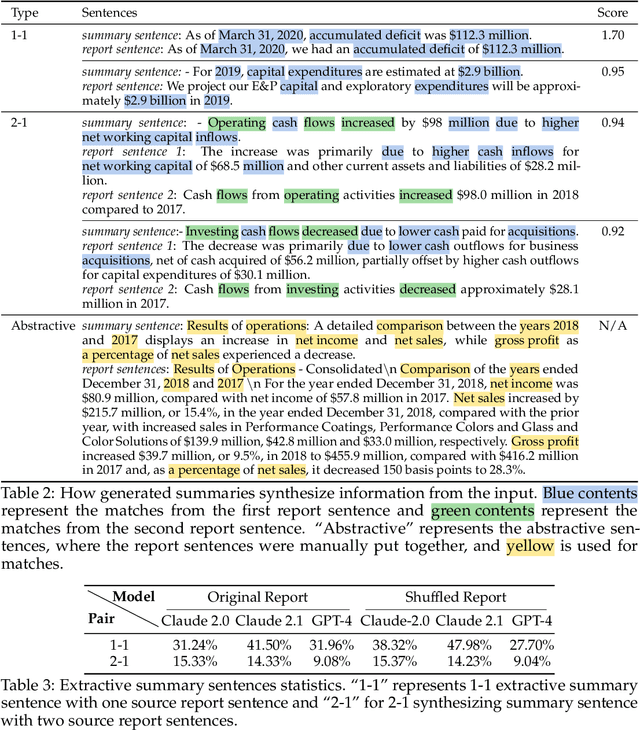
As large language models (LLMs) expand the power of natural language processing to handle long inputs, rigorous and systematic analyses are necessary to understand their abilities and behavior. A salient application is summarization, due to its ubiquity and controversy (e.g., researchers have declared the death of summarization). In this paper, we use financial report summarization as a case study because financial reports not only are long but also use numbers and tables extensively. We propose a computational framework for characterizing multimodal long-form summarization and investigate the behavior of Claude 2.0/2.1, GPT-4/3.5, and Command. We find that GPT-3.5 and Command fail to perform this summarization task meaningfully. For Claude 2 and GPT-4, we analyze the extractiveness of the summary and identify a position bias in LLMs. This position bias disappears after shuffling the input for Claude, which suggests that Claude has the ability to recognize important information. We also conduct a comprehensive investigation on the use of numeric data in LLM-generated summaries and offer a taxonomy of numeric hallucination. We employ prompt engineering to improve GPT-4's use of numbers with limited success. Overall, our analyses highlight the strong capability of Claude 2 in handling long multimodal inputs compared to GPT-4.

Surrogate Assisted Monte Carlo Tree Search in Combinatorial Optimization

Industries frequently adjust their facilities network by opening new branches in promising areas and closing branches in areas where they expect low profits. In this paper, we examine a particular class of facility location problems. Our objective is to minimize the loss of sales resulting from the removal of several retail stores. However, estimating sales accurately is expensive and time-consuming. To overcome this challenge, we leverage Monte Carlo Tree Search (MCTS) assisted by a surrogate model that computes evaluations faster. Results suggest that MCTS supported by a fast surrogate function can generate solutions faster while maintaining a consistent solution compared to MCTS that does not benefit from the surrogate function.

Balancing Fairness and Accuracy in Data-Restricted Binary Classification

Applications that deal with sensitive information may have restrictions placed on the data available to a machine learning (ML) classifier. For example, in some applications, a classifier may not have direct access to sensitive attributes, affecting its ability to produce accurate and fair decisions. This paper proposes a framework that models the trade-off between accuracy and fairness under four practical scenarios that dictate the type of data available for analysis. Prior works examine this trade-off by analyzing the outputs of a scoring function that has been trained to implicitly learn the underlying distribution of the feature vector, class label, and sensitive attribute of a dataset. In contrast, our framework directly analyzes the behavior of the optimal Bayesian classifier on this underlying distribution by constructing a discrete approximation it from the dataset itself. This approach enables us to formulate multiple convex optimization problems, which allow us to answer the question: How is the accuracy of a Bayesian classifier affected in different data restricting scenarios when constrained to be fair? Analysis is performed on a set of fairness definitions that include group and individual fairness. Experiments on three datasets demonstrate the utility of the proposed framework as a tool for quantifying the trade-offs among different fairness notions and their distributional dependencies.

Bounding the Excess Risk for Linear Models Trained on Marginal-Preserving, Differentially-Private, Synthetic Data

The growing use of machine learning (ML) has raised concerns that an ML model may reveal private information about an individual who has contributed to the training dataset. To prevent leakage of sensitive data, we consider using differentially-private (DP), synthetic training data instead of real training data to train an ML model. A key desirable property of synthetic data is its ability to preserve the low-order marginals of the original distribution. Our main contribution comprises novel upper and lower bounds on the excess empirical risk of linear models trained on such synthetic data, for continuous and Lipschitz loss functions. We perform extensive experimentation alongside our theoretical results.

A Canonical Data Transformation for Achieving Inter- and Within-group Fairness

Increases in the deployment of machine learning algorithms for applications that deal with sensitive data have brought attention to the issue of fairness in machine learning. Many works have been devoted to applications that require different demographic groups to be treated fairly. However, algorithms that aim to satisfy inter-group fairness (also called group fairness) may inadvertently treat individuals within the same demographic group unfairly. To address this issue, we introduce a formal definition of within-group fairness that maintains fairness among individuals from within the same group. We propose a pre-processing framework to meet both inter- and within-group fairness criteria with little compromise in accuracy. The framework maps the feature vectors of members from different groups to an inter-group-fair canonical domain before feeding them into a scoring function. The mapping is constructed to preserve the relative relationship between the scores obtained from the unprocessed feature vectors of individuals from the same demographic group, guaranteeing within-group fairness. We apply this framework to the COMPAS risk assessment and Law School datasets and compare its performance in achieving inter-group and within-group fairness to two regularization-based methods.