On the Connection between Game-Theoretic Feature Attributions and Counterfactual Explanations
Paper and Code
Jul 13, 2023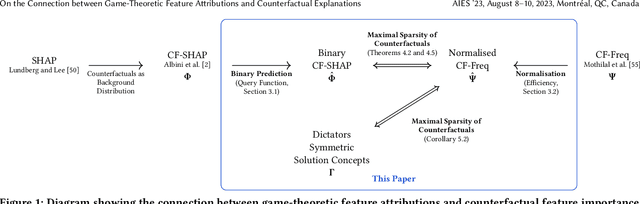


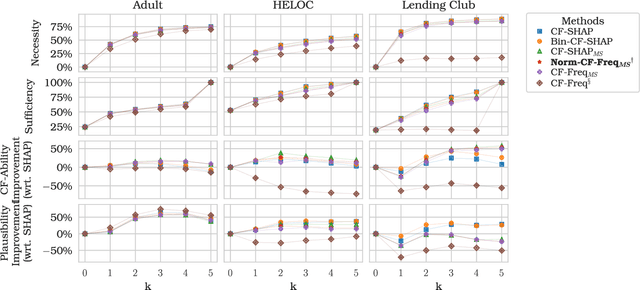
Explainable Artificial Intelligence (XAI) has received widespread interest in recent years, and two of the most popular types of explanations are feature attributions, and counterfactual explanations. These classes of approaches have been largely studied independently and the few attempts at reconciling them have been primarily empirical. This work establishes a clear theoretical connection between game-theoretic feature attributions, focusing on but not limited to SHAP, and counterfactuals explanations. After motivating operative changes to Shapley values based feature attributions and counterfactual explanations, we prove that, under conditions, they are in fact equivalent. We then extend the equivalency result to game-theoretic solution concepts beyond Shapley values. Moreover, through the analysis of the conditions of such equivalence, we shed light on the limitations of naively using counterfactual explanations to provide feature importances. Experiments on three datasets quantitatively show the difference in explanations at every stage of the connection between the two approaches and corroborate the theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge