Closure operators: Complexity and applications to classification and decision-making

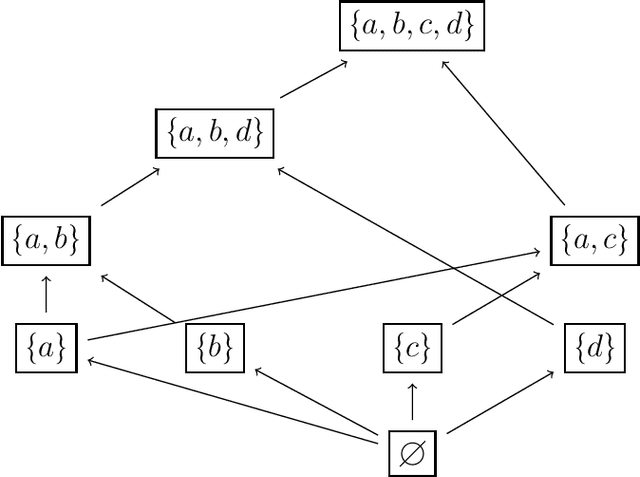
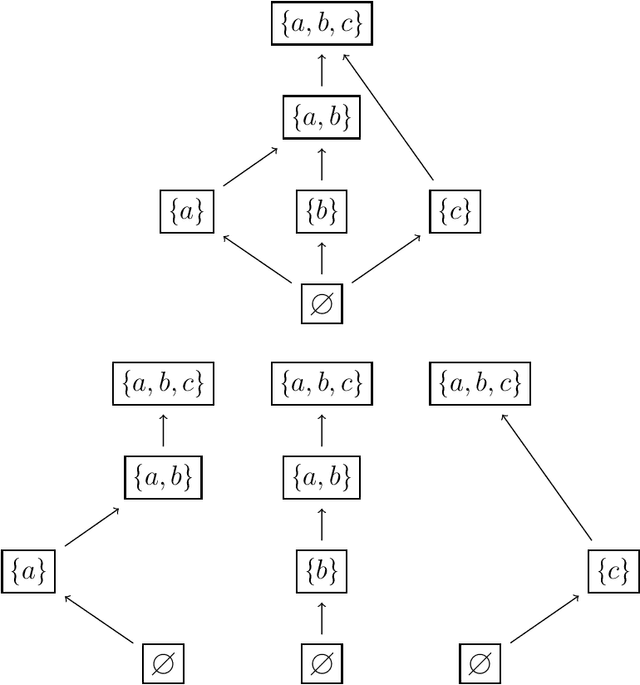
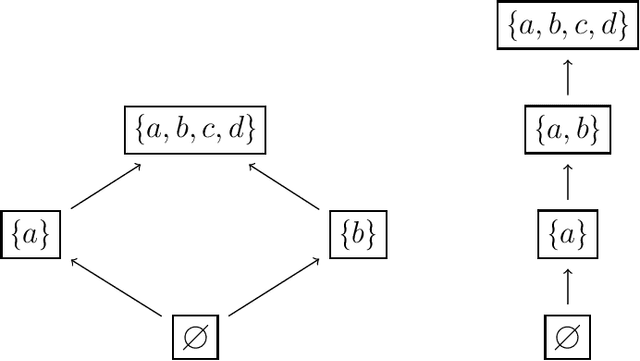
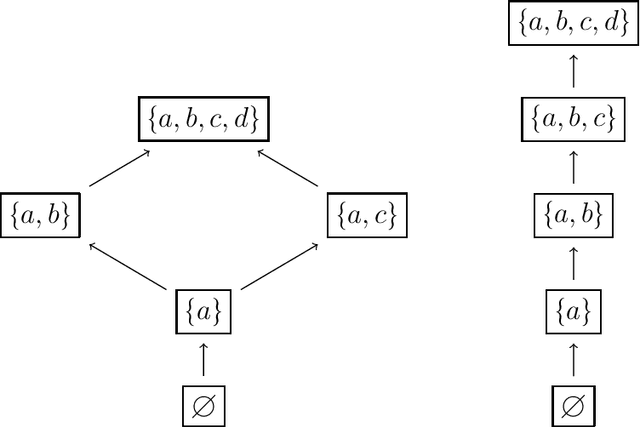
We study the complexity of closure operators, with applications to machine learning and decision theory. In machine learning, closure operators emerge naturally in data classification and clustering. In decision theory, they can model equivalence of choice menus, and therefore situations with a preference for flexibility. Our contribution is to formulate a notion of complexity of closure operators, which translate into the complexity of a classifier in ML, or of a utility function in decision theory.

Aggregation of Pareto optimal models

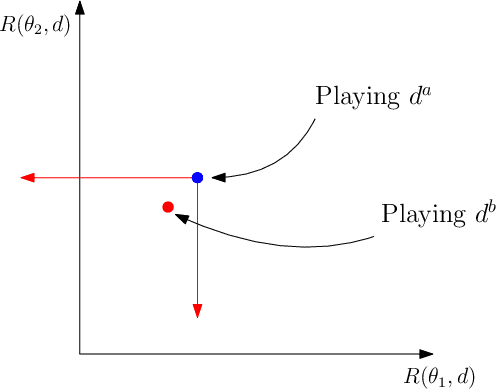
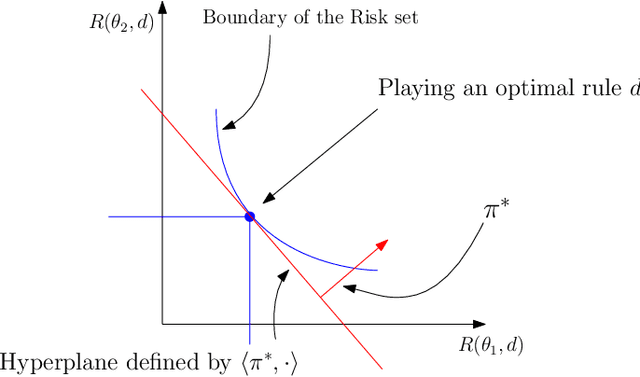
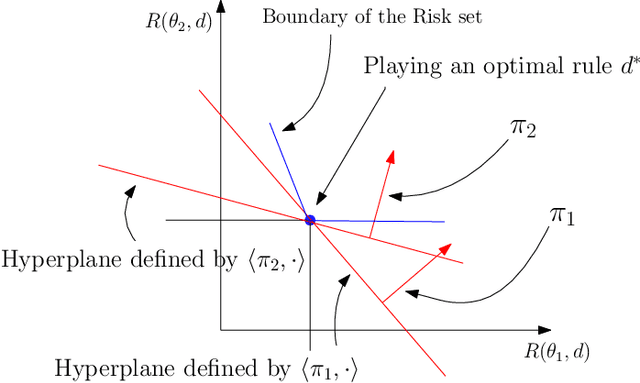
In statistical decision theory, a model is said to be Pareto optimal (or admissible) if no other model carries less risk for at least one state of nature while presenting no more risk for others. How can you rationally aggregate/combine a finite set of Pareto optimal models while preserving Pareto efficiency? This question is nontrivial because weighted model averaging does not, in general, preserve Pareto efficiency. This paper presents an answer in four logical steps: (1) A rational aggregation rule should preserve Pareto efficiency (2) Due to the complete class theorem, Pareto optimal models must be Bayesian, i.e., they minimize a risk where the true state of nature is averaged with respect to some prior. Therefore each Pareto optimal model can be associated with a prior, and Pareto efficiency can be maintained by aggregating Pareto optimal models through their priors. (3) A prior can be interpreted as a preference ranking over models: prior $\pi$ prefers model A over model B if the average risk of A is lower than the average risk of B. (4) A rational/consistent aggregation rule should preserve this preference ranking: If both priors $\pi$ and $\pi'$ prefer model A over model B, then the prior obtained by aggregating $\pi$ and $\pi'$ must also prefer A over B. Under these four steps, we show that all rational/consistent aggregation rules are as follows: Give each individual Pareto optimal model a weight, introduce a weak order/ranking over the set of Pareto optimal models, aggregate a finite set of models S as the model associated with the prior obtained as the weighted average of the priors of the highest-ranked models in S. This result shows that all rational/consistent aggregation rules must follow a generalization of hierarchical Bayesian modeling. Following our main result, we present applications to Kernel smoothing, time-depreciating models, and voting mechanisms.

Uncertainty Quantification of the 4th kind; optimal posterior accuracy-uncertainty tradeoff with the minimum enclosing ball

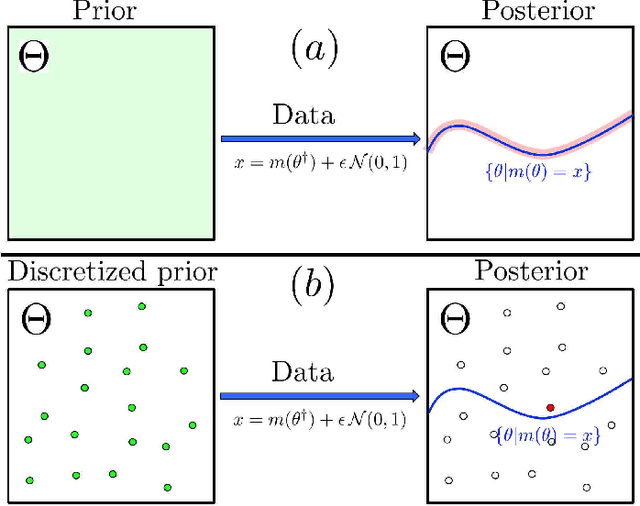
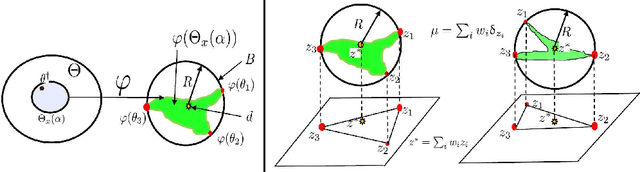
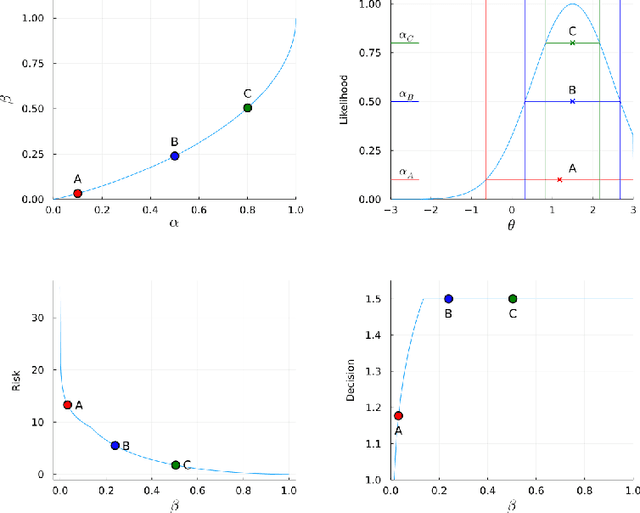
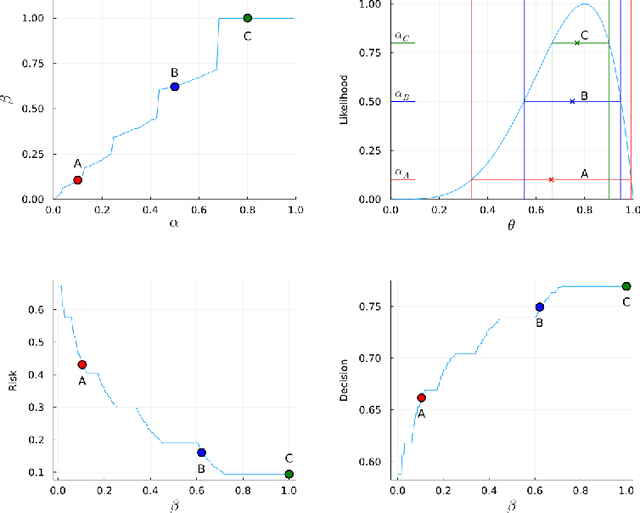
There are essentially three kinds of approaches to Uncertainty Quantification (UQ): (A) robust optimization, (B) Bayesian, (C) decision theory. Although (A) is robust, it is unfavorable with respect to accuracy and data assimilation. (B) requires a prior, it is generally brittle and posterior estimations can be slow. Although (C) leads to the identification of an optimal prior, its approximation suffers from the curse of dimensionality and the notion of risk is one that is averaged with respect to the distribution of the data. We introduce a 4th kind which is a hybrid between (A), (B), (C), and hypothesis testing. It can be summarized as, after observing a sample $x$, (1) defining a likelihood region through the relative likelihood and (2) playing a minmax game in that region to define optimal estimators and their risk. The resulting method has several desirable properties (a) an optimal prior is identified after measuring the data, and the notion of risk is a posterior one, (b) the determination of the optimal estimate and its risk can be reduced to computing the minimum enclosing ball of the image of the likelihood region under the quantity of interest map (which is fast and not subject to the curse of dimensionality). The method is characterized by a parameter in $ [0,1]$ acting as an assumed lower bound on the rarity of the observed data (the relative likelihood). When that parameter is near $1$, the method produces a posterior distribution concentrated around a maximum likelihood estimate with tight but low confidence UQ estimates. When that parameter is near $0$, the method produces a maximal risk posterior distribution with high confidence UQ estimates. In addition to navigating the accuracy-uncertainty tradeoff, the proposed method addresses the brittleness of Bayesian inference by navigating the robustness-accuracy tradeoff associated with data assimilation.

Decision Theoretic Bootstrapping

The design and testing of supervised machine learning models combine two fundamental distributions: (1) the training data distribution (2) the testing data distribution. Although these two distributions are identical and identifiable when the data set is infinite; they are imperfectly known (and possibly distinct) when the data is finite (and possibly corrupted) and this uncertainty must be taken into account for robust Uncertainty Quantification (UQ). We present a general decision-theoretic bootstrapping solution to this problem: (1) partition the available data into a training subset and a UQ subset (2) take $m$ subsampled subsets of the training set and train $m$ models (3) partition the UQ set into $n$ sorted subsets and take a random fraction of them to define $n$ corresponding empirical distributions $\mu_{j}$ (4) consider the adversarial game where Player I selects a model $i\in\left\{ 1,\ldots,m\right\} $, Player II selects the UQ distribution $\mu_{j}$ and Player I receives a loss defined by evaluating the model $i$ against data points sampled from $\mu_{j}$ (5) identify optimal mixed strategies (probability distributions over models and UQ distributions) for both players. These randomized optimal mixed strategies provide optimal model mixtures and UQ estimates given the adversarial uncertainty of the training and testing distributions represented by the game. The proposed approach provides (1) some degree of robustness to distributional shift in both the distribution of training data and that of the testing data (2) conditional probability distributions on the output space forming aleatory representations of the uncertainty on the output as a function of the input variable.