Uncertainty Quantification of the 4th kind; optimal posterior accuracy-uncertainty tradeoff with the minimum enclosing ball

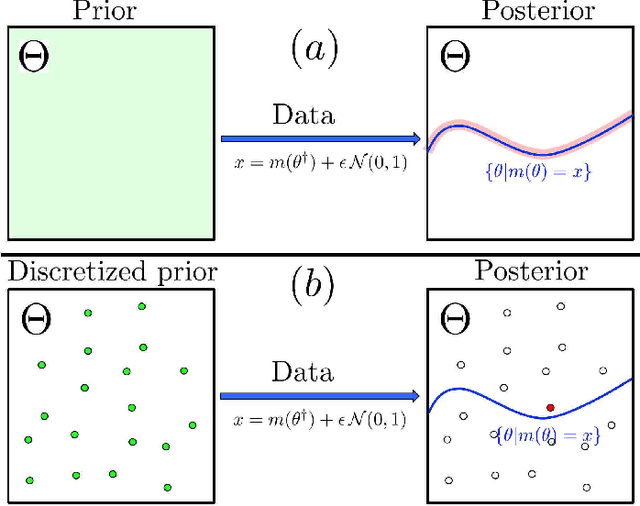
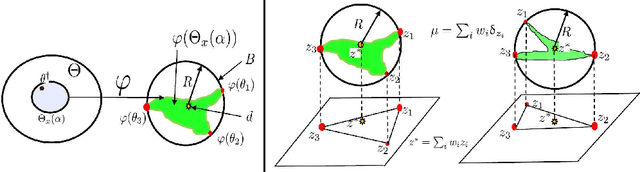
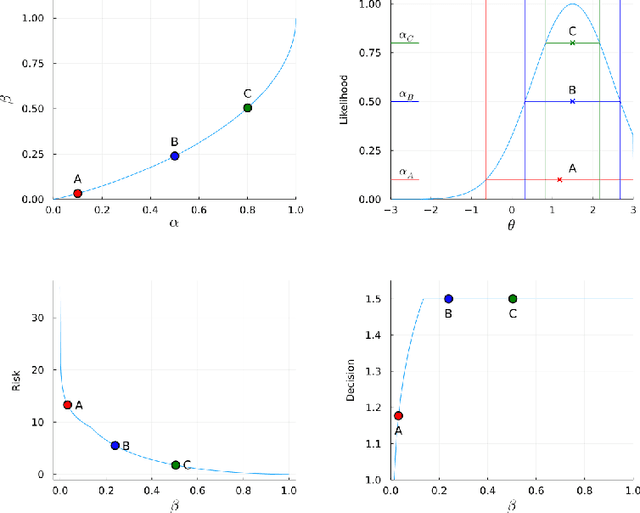
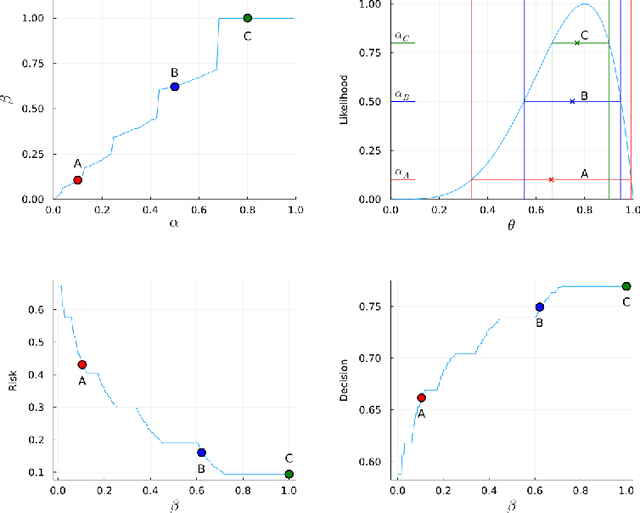
There are essentially three kinds of approaches to Uncertainty Quantification (UQ): (A) robust optimization, (B) Bayesian, (C) decision theory. Although (A) is robust, it is unfavorable with respect to accuracy and data assimilation. (B) requires a prior, it is generally brittle and posterior estimations can be slow. Although (C) leads to the identification of an optimal prior, its approximation suffers from the curse of dimensionality and the notion of risk is one that is averaged with respect to the distribution of the data. We introduce a 4th kind which is a hybrid between (A), (B), (C), and hypothesis testing. It can be summarized as, after observing a sample $x$, (1) defining a likelihood region through the relative likelihood and (2) playing a minmax game in that region to define optimal estimators and their risk. The resulting method has several desirable properties (a) an optimal prior is identified after measuring the data, and the notion of risk is a posterior one, (b) the determination of the optimal estimate and its risk can be reduced to computing the minimum enclosing ball of the image of the likelihood region under the quantity of interest map (which is fast and not subject to the curse of dimensionality). The method is characterized by a parameter in $ [0,1]$ acting as an assumed lower bound on the rarity of the observed data (the relative likelihood). When that parameter is near $1$, the method produces a posterior distribution concentrated around a maximum likelihood estimate with tight but low confidence UQ estimates. When that parameter is near $0$, the method produces a maximal risk posterior distribution with high confidence UQ estimates. In addition to navigating the accuracy-uncertainty tradeoff, the proposed method addresses the brittleness of Bayesian inference by navigating the robustness-accuracy tradeoff associated with data assimilation.

Kernel Mode Decomposition and programmable/interpretable regression networks

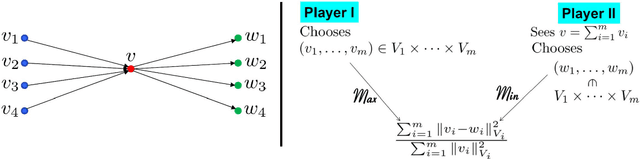
Mode decomposition is a prototypical pattern recognition problem that can be addressed from the (a priori distinct) perspectives of numerical approximation, statistical inference and deep learning. Could its analysis through these combined perspectives be used as a Rosetta stone for deciphering mechanisms at play in deep learning? Motivated by this question we introduce programmable and interpretable regression networks for pattern recognition and address mode decomposition as a prototypical problem. The programming of these networks is achieved by assembling elementary modules decomposing and recomposing kernels and data. These elementary steps are repeated across levels of abstraction and interpreted from the equivalent perspectives of optimal recovery, game theory and Gaussian process regression (GPR). The prototypical mode/kernel decomposition module produces an optimal approximation $(w_1,w_2,\cdots,w_m)$ of an element $(v_1,v_2,\ldots,v_m)$ of a product of Hilbert subspaces of a common Hilbert space from the observation of the sum $v:=v_1+\cdots+v_m$. The prototypical mode/kernel recomposition module performs partial sums of the recovered modes $w_i$ based on the alignment between each recovered mode $w_i$ and the data $v$. We illustrate the proposed framework by programming regression networks approximating the modes $v_i= a_i(t)y_i\big(\theta_i(t)\big)$ of a (possibly noisy) signal $\sum_i v_i$ when the amplitudes $a_i$, instantaneous phases $\theta_i$ and periodic waveforms $y_i$ may all be unknown and show near machine precision recovery under regularity and separation assumptions on the instantaneous amplitudes $a_i$ and frequencies $\dot{\theta}_i$. The structure of some of these networks share intriguing similarities with convolutional neural networks while being interpretable, programmable and amenable to theoretical analysis.

Universal Scalable Robust Solvers from Computational Information Games and fast eigenspace adapted Multiresolution Analysis

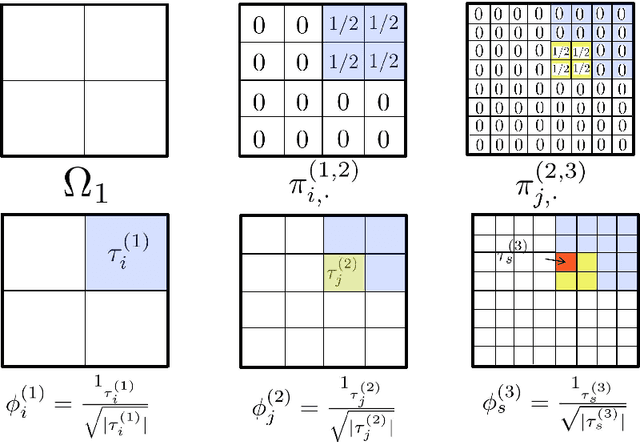
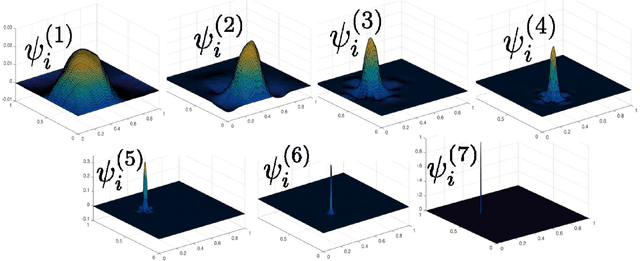
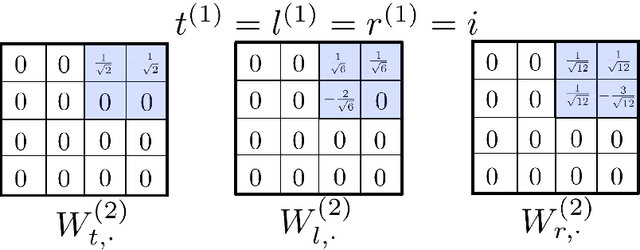
We show how the discovery of robust scalable numerical solvers for arbitrary bounded linear operators can be automated as a Game Theory problem by reformulating the process of computing with partial information and limited resources as that of playing underlying hierarchies of adversarial information games. When the solution space is a Banach space $B$ endowed with a quadratic norm $\|\cdot\|$, the optimal measure (mixed strategy) for such games (e.g. the adversarial recovery of $u\in B$, given partial measurements $[\phi_i, u]$ with $\phi_i\in B^*$, using relative error in $\|\cdot\|$-norm as a loss) is a centered Gaussian field $\xi$ solely determined by the norm $\|\cdot\|$, whose conditioning (on measurements) produces optimal bets. When measurements are hierarchical, the process of conditioning this Gaussian field produces a hierarchy of elementary bets (gamblets). These gamblets generalize the notion of Wavelets and Wannier functions in the sense that they are adapted to the norm $\|\cdot\|$ and induce a multi-resolution decomposition of $B$ that is adapted to the eigensubspaces of the operator defining the norm $\|\cdot\|$. When the operator is localized, we show that the resulting gamblets are localized both in space and frequency and introduce the Fast Gamblet Transform (FGT) with rigorous accuracy and (near-linear) complexity estimates. As the FFT can be used to solve and diagonalize arbitrary PDEs with constant coefficients, the FGT can be used to decompose a wide range of continuous linear operators (including arbitrary continuous linear bijections from $H^s_0$ to $H^{-s}$ or to $L^2$) into a sequence of independent linear systems with uniformly bounded condition numbers and leads to $\mathcal{O}(N \operatorname{polylog} N)$ solvers and eigenspace adapted Multiresolution Analysis (resulting in near linear complexity approximation of all eigensubspaces).

Towards Machine Wald

The past century has seen a steady increase in the need of estimating and predicting complex systems and making (possibly critical) decisions with limited information. Although computers have made possible the numerical evaluation of sophisticated statistical models, these models are still designed \emph{by humans} because there is currently no known recipe or algorithm for dividing the design of a statistical model into a sequence of arithmetic operations. Indeed enabling computers to \emph{think} as \emph{humans} have the ability to do when faced with uncertainty is challenging in several major ways: (1) Finding optimal statistical models remains to be formulated as a well posed problem when information on the system of interest is incomplete and comes in the form of a complex combination of sample data, partial knowledge of constitutive relations and a limited description of the distribution of input random variables. (2) The space of admissible scenarios along with the space of relevant information, assumptions, and/or beliefs, tend to be infinite dimensional, whereas calculus on a computer is necessarily discrete and finite. With this purpose, this paper explores the foundations of a rigorous framework for the scientific computation of optimal statistical estimators/models and reviews their connections with Decision Theory, Machine Learning, Bayesian Inference, Stochastic Optimization, Robust Optimization, Optimal Uncertainty Quantification and Information Based Complexity.

Fast rates for support vector machines using Gaussian kernels

For binary classification we establish learning rates up to the order of $n^{-1}$ for support vector machines (SVMs) with hinge loss and Gaussian RBF kernels. These rates are in terms of two assumptions on the considered distributions: Tsybakov's noise assumption to establish a small estimation error, and a new geometric noise condition which is used to bound the approximation error. Unlike previously proposed concepts for bounding the approximation error, the geometric noise assumption does not employ any smoothness assumption.

Learning from dependent observations

In most papers establishing consistency for learning algorithms it is assumed that the observations used for training are realizations of an i.i.d. process. In this paper we go far beyond this classical framework by showing that support vector machines (SVMs) essentially only require that the data-generating process satisfies a certain law of large numbers. We then consider the learnability of SVMs for $\a$-mixing (not necessarily stationary) processes for both classification and regression, where for the latter we explicitly allow unbounded noise.

Bayesian Stratified Sampling to Assess Corpus Utility

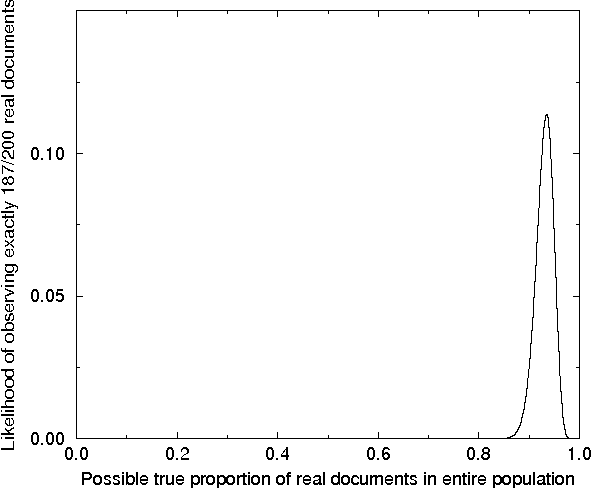
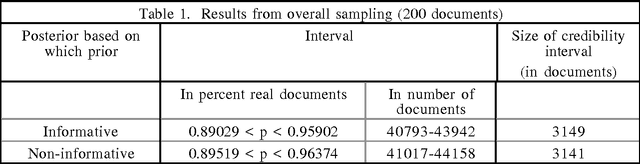
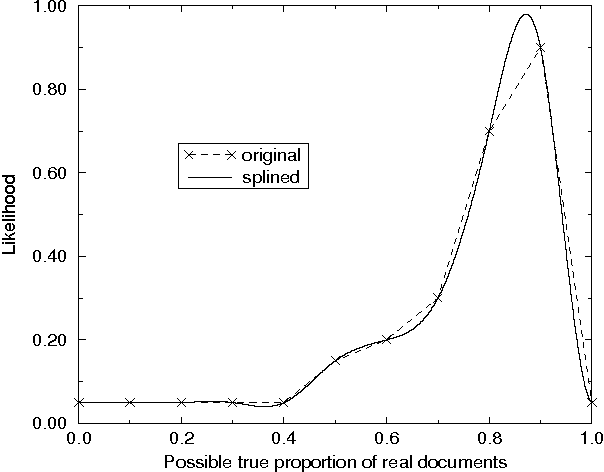
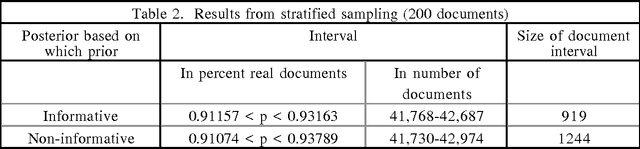
This paper describes a method for asking statistical questions about a large text corpus. We exemplify the method by addressing the question, "What percentage of Federal Register documents are real documents, of possible interest to a text researcher or analyst?" We estimate an answer to this question by evaluating 200 documents selected from a corpus of 45,820 Federal Register documents. Stratified sampling is used to reduce the sampling uncertainty of the estimate from over 3100 documents to fewer than 1000. The stratification is based on observed characteristics of real documents, while the sampling procedure incorporates a Bayesian version of Neyman allocation. A possible application of the method is to establish baseline statistics used to estimate recall rates for information retrieval systems.