Kernel Mode Decomposition and programmable/interpretable regression networks
Paper and Code
Jul 19, 2019

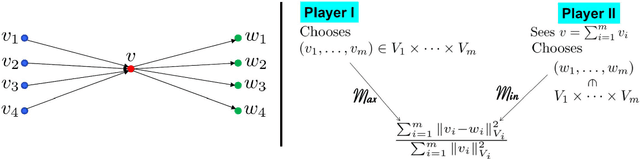

Mode decomposition is a prototypical pattern recognition problem that can be addressed from the (a priori distinct) perspectives of numerical approximation, statistical inference and deep learning. Could its analysis through these combined perspectives be used as a Rosetta stone for deciphering mechanisms at play in deep learning? Motivated by this question we introduce programmable and interpretable regression networks for pattern recognition and address mode decomposition as a prototypical problem. The programming of these networks is achieved by assembling elementary modules decomposing and recomposing kernels and data. These elementary steps are repeated across levels of abstraction and interpreted from the equivalent perspectives of optimal recovery, game theory and Gaussian process regression (GPR). The prototypical mode/kernel decomposition module produces an optimal approximation $(w_1,w_2,\cdots,w_m)$ of an element $(v_1,v_2,\ldots,v_m)$ of a product of Hilbert subspaces of a common Hilbert space from the observation of the sum $v:=v_1+\cdots+v_m$. The prototypical mode/kernel recomposition module performs partial sums of the recovered modes $w_i$ based on the alignment between each recovered mode $w_i$ and the data $v$. We illustrate the proposed framework by programming regression networks approximating the modes $v_i= a_i(t)y_i\big(\theta_i(t)\big)$ of a (possibly noisy) signal $\sum_i v_i$ when the amplitudes $a_i$, instantaneous phases $\theta_i$ and periodic waveforms $y_i$ may all be unknown and show near machine precision recovery under regularity and separation assumptions on the instantaneous amplitudes $a_i$ and frequencies $\dot{\theta}_i$. The structure of some of these networks share intriguing similarities with convolutional neural networks while being interpretable, programmable and amenable to theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge