Deep regularization and direct training of the inner layers of Neural Networks with Kernel Flows

We introduce a new regularization method for Artificial Neural Networks (ANNs) based on Kernel Flows (KFs). KFs were introduced as a method for kernel selection in regression/kriging based on the minimization of the loss of accuracy incurred by halving the number of interpolation points in random batches of the dataset. Writing $f_\theta(x) = \big(f^{(n)}_{\theta_n}\circ f^{(n-1)}_{\theta_{n-1}} \circ \dots \circ f^{(1)}_{\theta_1}\big)(x)$ for the functional representation of compositional structure of the ANN, the inner layers outputs $h^{(i)}(x) = \big(f^{(i)}_{\theta_i}\circ f^{(i-1)}_{\theta_{i-1}} \circ \dots \circ f^{(1)}_{\theta_1}\big)(x)$ define a hierarchy of feature maps and kernels $k^{(i)}(x,x')=\exp(- \gamma_i \|h^{(i)}(x)-h^{(i)}(x')\|_2^2)$. When combined with a batch of the dataset these kernels produce KF losses $e_2^{(i)}$ (the $L^2$ regression error incurred by using a random half of the batch to predict the other half) depending on parameters of inner layers $\theta_1,\ldots,\theta_i$ (and $\gamma_i$). The proposed method simply consists in aggregating a subset of these KF losses with a classical output loss. We test the proposed method on CNNs and WRNs without alteration of structure nor output classifier and report reduced test errors, decreased generalization gaps, and increased robustness to distribution shift without significant increase in computational complexity. We suspect that these results might be explained by the fact that while conventional training only employs a linear functional (a generalized moment) of the empirical distribution defined by the dataset and can be prone to trapping in the Neural Tangent Kernel regime (under over-parameterizations), the proposed loss function (defined as a nonlinear functional of the empirical distribution) effectively trains the underlying kernel defined by the CNN beyond regressing the data with that kernel.

Kernel Mode Decomposition and programmable/interpretable regression networks

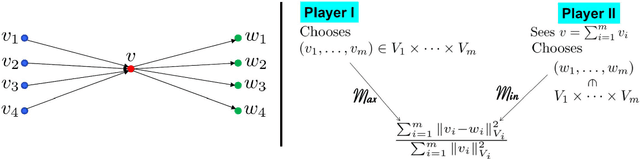
Mode decomposition is a prototypical pattern recognition problem that can be addressed from the (a priori distinct) perspectives of numerical approximation, statistical inference and deep learning. Could its analysis through these combined perspectives be used as a Rosetta stone for deciphering mechanisms at play in deep learning? Motivated by this question we introduce programmable and interpretable regression networks for pattern recognition and address mode decomposition as a prototypical problem. The programming of these networks is achieved by assembling elementary modules decomposing and recomposing kernels and data. These elementary steps are repeated across levels of abstraction and interpreted from the equivalent perspectives of optimal recovery, game theory and Gaussian process regression (GPR). The prototypical mode/kernel decomposition module produces an optimal approximation $(w_1,w_2,\cdots,w_m)$ of an element $(v_1,v_2,\ldots,v_m)$ of a product of Hilbert subspaces of a common Hilbert space from the observation of the sum $v:=v_1+\cdots+v_m$. The prototypical mode/kernel recomposition module performs partial sums of the recovered modes $w_i$ based on the alignment between each recovered mode $w_i$ and the data $v$. We illustrate the proposed framework by programming regression networks approximating the modes $v_i= a_i(t)y_i\big(\theta_i(t)\big)$ of a (possibly noisy) signal $\sum_i v_i$ when the amplitudes $a_i$, instantaneous phases $\theta_i$ and periodic waveforms $y_i$ may all be unknown and show near machine precision recovery under regularity and separation assumptions on the instantaneous amplitudes $a_i$ and frequencies $\dot{\theta}_i$. The structure of some of these networks share intriguing similarities with convolutional neural networks while being interpretable, programmable and amenable to theoretical analysis.

Kernel Flows: from learning kernels from data into the abyss

Learning can be seen as approximating an unknown function by interpolating the training data. Kriging offers a solution to this problem based on the prior specification of a kernel. We explore a numerical approximation approach to kernel selection/construction based on the simple premise that a kernel must be good if the number of interpolation points can be halved without significant loss in accuracy (measured using the intrinsic RKHS norm $\|\cdot\|$ associated with the kernel). We first test and motivate this idea on a simple problem of recovering the Green's function of an elliptic PDE (with inhomogeneous coefficients) from the sparse observation of one of its solutions. Next we consider the problem of learning non-parametric families of deep kernels of the form $K_1(F_n(x),F_n(x'))$ with $F_{n+1}=(I_d+\epsilon G_{n+1})\circ F_n$ and $G_{n+1} \in \operatorname{Span}\{K_1(F_n(x_i),\cdot)\}$. With the proposed approach constructing the kernel becomes equivalent to integrating a stochastic data driven dynamical system, which allows for the training of very deep (bottomless) networks and the exploration of their properties. These networks learn by constructing flow maps in the kernel and input spaces via incremental data-dependent deformations/perturbations (appearing as the cooperative counterpart of adversarial examples) and, at profound depths, they (1) can achieve accurate classification from only one data point per class (2) appear to learn archetypes of each class (3) expand distances between points that are in different classes and contract distances between points in the same class. For kernels parameterized by the weights of Convolutional Neural Networks, minimizing approximation errors incurred by halving random subsets of interpolation points, appears to outperform training (the same CNN architecture) with relative entropy and dropout.