Universal Scalable Robust Solvers from Computational Information Games and fast eigenspace adapted Multiresolution Analysis
Paper and Code
May 29, 2017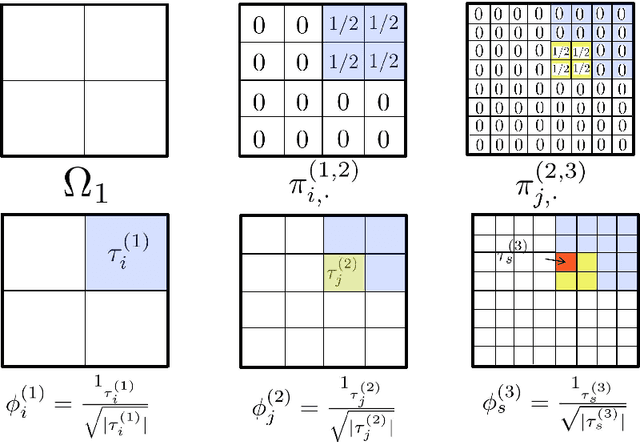

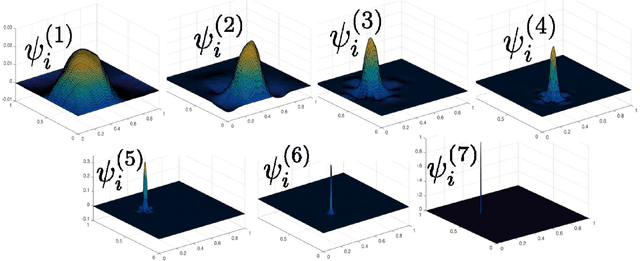
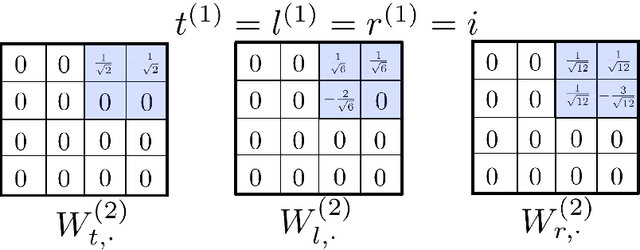
We show how the discovery of robust scalable numerical solvers for arbitrary bounded linear operators can be automated as a Game Theory problem by reformulating the process of computing with partial information and limited resources as that of playing underlying hierarchies of adversarial information games. When the solution space is a Banach space $B$ endowed with a quadratic norm $\|\cdot\|$, the optimal measure (mixed strategy) for such games (e.g. the adversarial recovery of $u\in B$, given partial measurements $[\phi_i, u]$ with $\phi_i\in B^*$, using relative error in $\|\cdot\|$-norm as a loss) is a centered Gaussian field $\xi$ solely determined by the norm $\|\cdot\|$, whose conditioning (on measurements) produces optimal bets. When measurements are hierarchical, the process of conditioning this Gaussian field produces a hierarchy of elementary bets (gamblets). These gamblets generalize the notion of Wavelets and Wannier functions in the sense that they are adapted to the norm $\|\cdot\|$ and induce a multi-resolution decomposition of $B$ that is adapted to the eigensubspaces of the operator defining the norm $\|\cdot\|$. When the operator is localized, we show that the resulting gamblets are localized both in space and frequency and introduce the Fast Gamblet Transform (FGT) with rigorous accuracy and (near-linear) complexity estimates. As the FFT can be used to solve and diagonalize arbitrary PDEs with constant coefficients, the FGT can be used to decompose a wide range of continuous linear operators (including arbitrary continuous linear bijections from $H^s_0$ to $H^{-s}$ or to $L^2$) into a sequence of independent linear systems with uniformly bounded condition numbers and leads to $\mathcal{O}(N \operatorname{polylog} N)$ solvers and eigenspace adapted Multiresolution Analysis (resulting in near linear complexity approximation of all eigensubspaces).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge