Deep Learning with Kernel Flow Regularization for Time Series Forecasting

Long Short-Term Memory (LSTM) neural networks have been widely used for time series forecasting problems. However, LSTMs are prone to overfitting and performance reduction during test phases. Several different regularization techniques have been shown in literature to prevent overfitting problems in neural networks. In this paper, first, we introduce application of kernel flow methods for time series forecasting in general. Afterward, we examine the effectiveness of applying kernel flow regularization on LSTM layers to avoid overfitting problems. We describe a regularization method by applying kernel flow loss function on LSTM layers. In experimental results, we show that kernel flow outperforms baseline models on time series forecasting benchmarks. We also compare the effect of dropout and kernel flow regularization techniques on LSTMs. The experimental results illustrate that kernel flow achieves similar regularization effect to dropout. It also shows that the best results is obtained using both kernel flow and dropout regularizations with early stopping on LSTM layers on some time series datasets (e.g. power-load demand forecasts).

Uncertainty Quantification of the 4th kind; optimal posterior accuracy-uncertainty tradeoff with the minimum enclosing ball

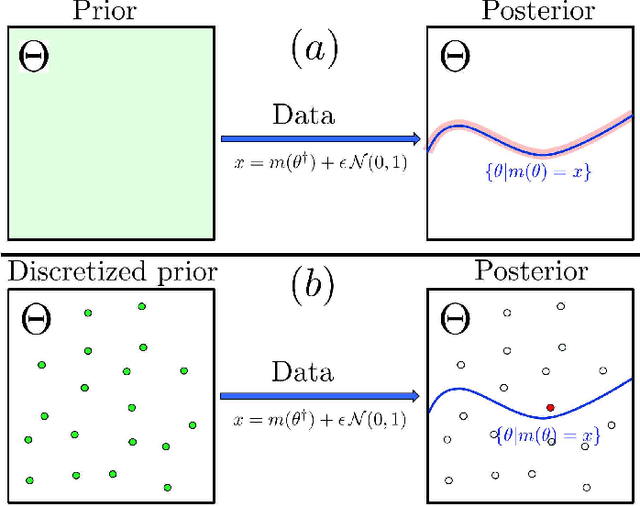
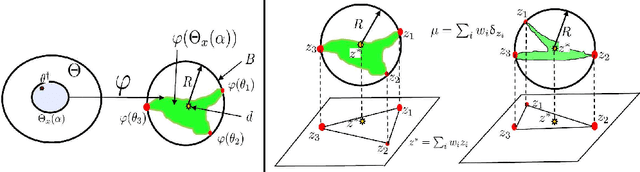
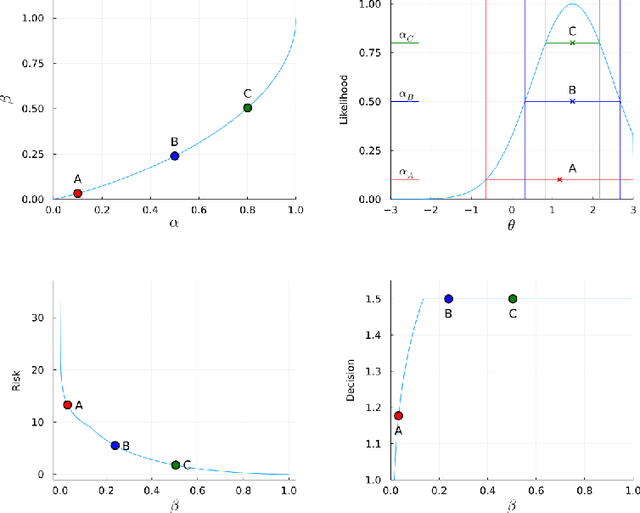
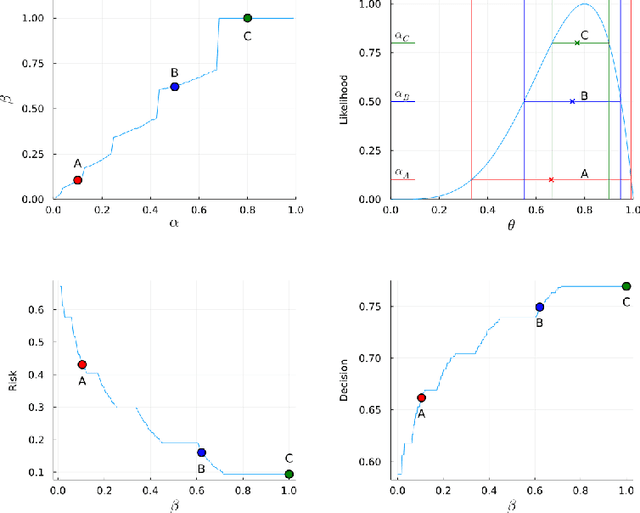
There are essentially three kinds of approaches to Uncertainty Quantification (UQ): (A) robust optimization, (B) Bayesian, (C) decision theory. Although (A) is robust, it is unfavorable with respect to accuracy and data assimilation. (B) requires a prior, it is generally brittle and posterior estimations can be slow. Although (C) leads to the identification of an optimal prior, its approximation suffers from the curse of dimensionality and the notion of risk is one that is averaged with respect to the distribution of the data. We introduce a 4th kind which is a hybrid between (A), (B), (C), and hypothesis testing. It can be summarized as, after observing a sample $x$, (1) defining a likelihood region through the relative likelihood and (2) playing a minmax game in that region to define optimal estimators and their risk. The resulting method has several desirable properties (a) an optimal prior is identified after measuring the data, and the notion of risk is a posterior one, (b) the determination of the optimal estimate and its risk can be reduced to computing the minimum enclosing ball of the image of the likelihood region under the quantity of interest map (which is fast and not subject to the curse of dimensionality). The method is characterized by a parameter in $ [0,1]$ acting as an assumed lower bound on the rarity of the observed data (the relative likelihood). When that parameter is near $1$, the method produces a posterior distribution concentrated around a maximum likelihood estimate with tight but low confidence UQ estimates. When that parameter is near $0$, the method produces a maximal risk posterior distribution with high confidence UQ estimates. In addition to navigating the accuracy-uncertainty tradeoff, the proposed method addresses the brittleness of Bayesian inference by navigating the robustness-accuracy tradeoff associated with data assimilation.