Kernel Methods for the Approximation of the Eigenfunctions of the Koopman Operator

The Koopman operator provides a linear framework to study nonlinear dynamical systems. Its spectra offer valuable insights into system dynamics, but the operator can exhibit both discrete and continuous spectra, complicating direct computations. In this paper, we introduce a kernel-based method to construct the principal eigenfunctions of the Koopman operator without explicitly computing the operator itself. These principal eigenfunctions are associated with the equilibrium dynamics, and their eigenvalues match those of the linearization of the nonlinear system at the equilibrium point. We exploit the structure of the principal eigenfunctions by decomposing them into linear and nonlinear components. The linear part corresponds to the left eigenvector of the system's linearization at the equilibrium, while the nonlinear part is obtained by solving a partial differential equation (PDE) using kernel methods. Our approach avoids common issues such as spectral pollution and spurious eigenvalues, which can arise in previous methods. We demonstrate the effectiveness of our algorithm through numerical examples.

Learning dynamical systems from data: A simple cross-validation perspective, part III: Irregularly-Sampled Time Series

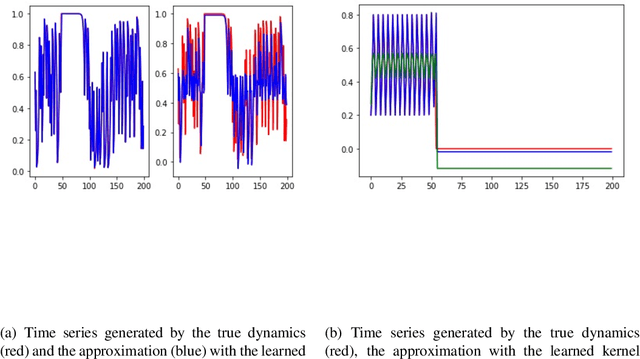
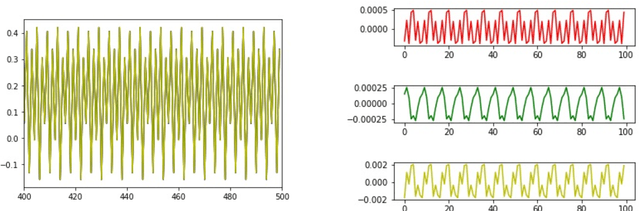
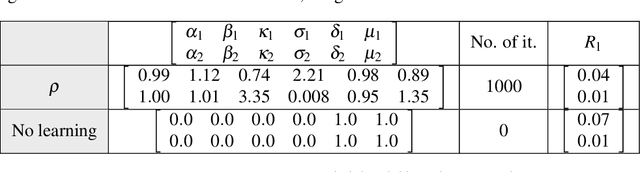
A simple and interpretable way to learn a dynamical system from data is to interpolate its vector-field with a kernel. In particular, this strategy is highly efficient (both in terms of accuracy and complexity) when the kernel is data-adapted using Kernel Flows (KF)~\cite{Owhadi19} (which uses gradient-based optimization to learn a kernel based on the premise that a kernel is good if there is no significant loss in accuracy if half of the data is used for interpolation). Despite its previous successes, this strategy (based on interpolating the vector field driving the dynamical system) breaks down when the observed time series is not regularly sampled in time. In this work, we propose to address this problem by directly approximating the vector field of the dynamical system by incorporating time differences between observations in the (KF) data-adapted kernels. We compare our approach with the classical one over different benchmark dynamical systems and show that it significantly improves the forecasting accuracy while remaining simple, fast, and robust.