Self-Normalized Resets for Plasticity in Continual Learning

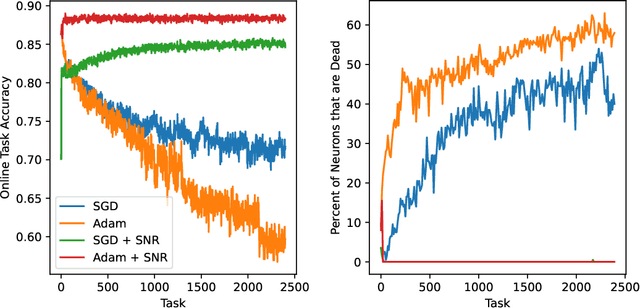
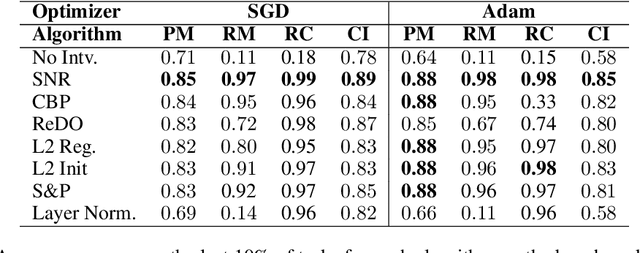
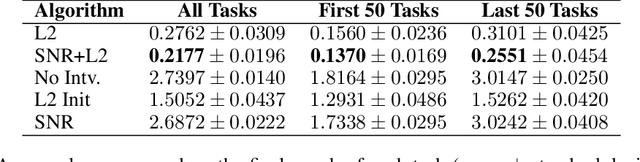
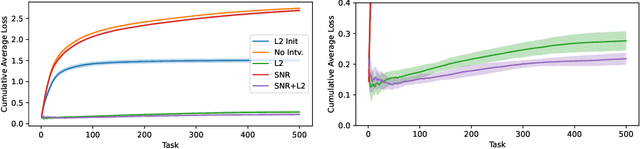
Plasticity Loss is an increasingly important phenomenon that refers to the empirical observation that as a neural network is continually trained on a sequence of changing tasks, its ability to adapt to a new task diminishes over time. We introduce Self-Normalized Resets (SNR), a simple adaptive algorithm that mitigates plasticity loss by resetting a neuron's weights when evidence suggests its firing rate has effectively dropped to zero. Across a battery of continual learning problems and network architectures, we demonstrate that SNR consistently attains superior performance compared to its competitor algorithms. We also demonstrate that SNR is robust to its sole hyperparameter, its rejection percentile threshold, while competitor algorithms show significant sensitivity. SNR's threshold-based reset mechanism is motivated by a simple hypothesis test that we derive. Seen through the lens of this hypothesis test, competing reset proposals yield suboptimal error rates in correctly detecting inactive neurons, potentially explaining our experimental observations. We also conduct a theoretical investigation of the optimization landscape for the problem of learning a single ReLU. We show that even when initialized adversarially, an idealized version of SNR learns the target ReLU, while regularization-based approaches can fail to learn.

Correcting for Interference in Experiments: A Case Study at Douyin

Interference is a ubiquitous problem in experiments conducted on two-sided content marketplaces, such as Douyin (China's analog of TikTok). In many cases, creators are the natural unit of experimentation, but creators interfere with each other through competition for viewers' limited time and attention. "Naive" estimators currently used in practice simply ignore the interference, but in doing so incur bias on the order of the treatment effect. We formalize the problem of inference in such experiments as one of policy evaluation. Off-policy estimators, while unbiased, are impractically high variance. We introduce a novel Monte-Carlo estimator, based on "Differences-in-Qs" (DQ) techniques, which achieves bias that is second-order in the treatment effect, while remaining sample-efficient to estimate. On the theoretical side, our contribution is to develop a generalized theory of Taylor expansions for policy evaluation, which extends DQ theory to all major MDP formulations. On the practical side, we implement our estimator on Douyin's experimentation platform, and in the process develop DQ into a truly "plug-and-play" estimator for interference in real-world settings: one which provides robust, low-bias, low-variance treatment effect estimates; admits computationally cheap, asymptotically exact uncertainty quantification; and reduces MSE by 99\% compared to the best existing alternatives in our applications.

Policy Optimization for Personalized Interventions in Behavioral Health

Problem definition: Behavioral health interventions, delivered through digital platforms, have the potential to significantly improve health outcomes, through education, motivation, reminders, and outreach. We study the problem of optimizing personalized interventions for patients to maximize some long-term outcome, in a setting where interventions are costly and capacity-constrained. Methodology/results: This paper provides a model-free approach to solving this problem. We find that generic model-free approaches from the reinforcement learning literature are too data intensive for healthcare applications, while simpler bandit approaches make progress at the expense of ignoring long-term patient dynamics. We present a new algorithm we dub DecompPI that approximates one step of policy iteration. Implementing DecompPI simply consists of a prediction task from offline data, alleviating the need for online experimentation. Theoretically, we show that under a natural set of structural assumptions on patient dynamics, DecompPI surprisingly recovers at least 1/2 of the improvement possible between a naive baseline policy and the optimal policy. At the same time, DecompPI is both robust to estimation errors and interpretable. Through an empirical case study on a mobile health platform for improving treatment adherence for tuberculosis, we find that DecompPI can provide the same efficacy as the status quo with approximately half the capacity of interventions. Managerial implications: DecompPI is general and is easily implementable for organizations aiming to improve long-term behavior through targeted interventions. Our case study suggests that the platform's costs of deploying interventions can potentially be cut by 50%, which facilitates the ability to scale up the system in a cost-efficient fashion.

Markovian Interference in Experiments

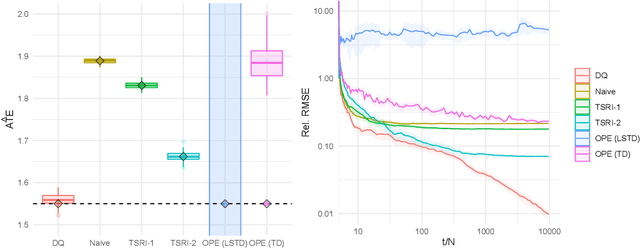
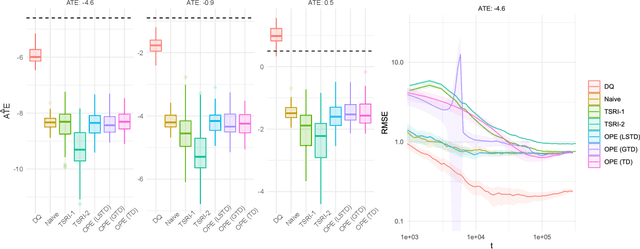
We consider experiments in dynamical systems where interventions on some experimental units impact other units through a limiting constraint (such as a limited inventory). Despite outsize practical importance, the best estimators for this `Markovian' interference problem are largely heuristic in nature, and their bias is not well understood. We formalize the problem of inference in such experiments as one of policy evaluation. Off-policy estimators, while unbiased, apparently incur a large penalty in variance relative to state-of-the-art heuristics. We introduce an on-policy estimator: the Differences-In-Q's (DQ) estimator. We show that the DQ estimator can in general have exponentially smaller variance than off-policy evaluation. At the same time, its bias is second order in the impact of the intervention. This yields a striking bias-variance tradeoff so that the DQ estimator effectively dominates state-of-the-art alternatives. From a theoretical perspective, we introduce three separate novel techniques that are of independent interest in the theory of Reinforcement Learning (RL). Our empirical evaluation includes a set of experiments on a city-scale ride-hailing simulator.

Uncertainty Quantification For Low-Rank Matrix Completion With Heterogeneous and Sub-Exponential Noise

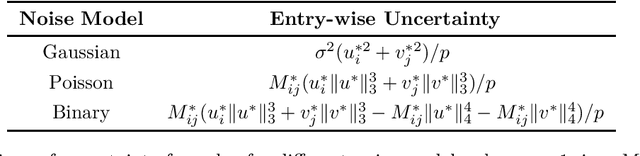
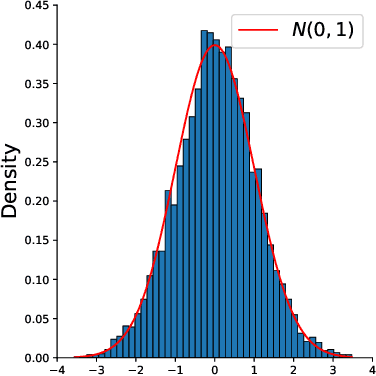
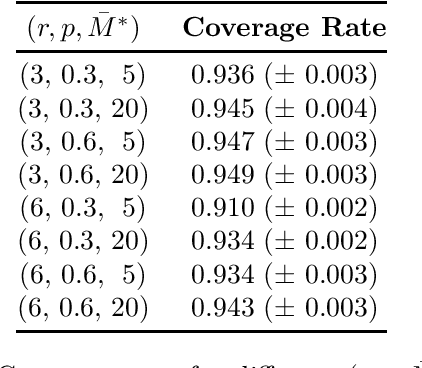
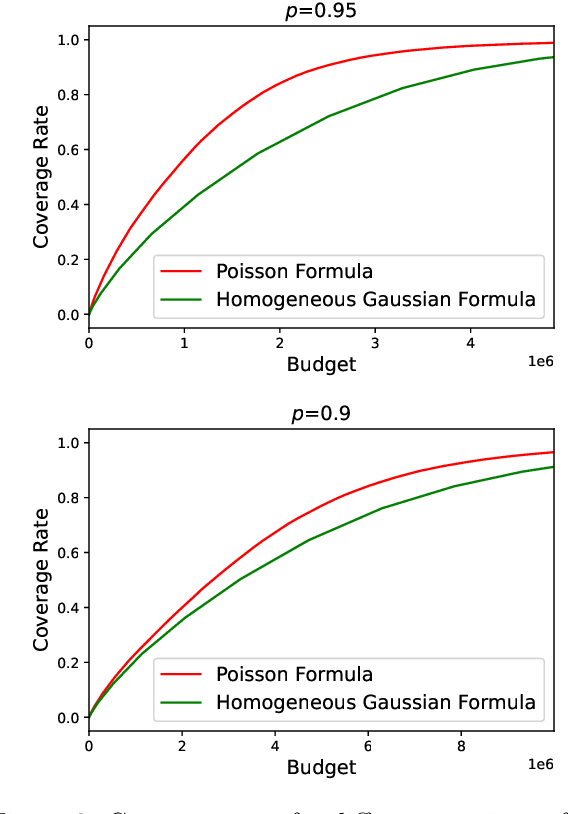
The problem of low-rank matrix completion with heterogeneous and sub-exponential (as opposed to homogeneous and Gaussian) noise is particularly relevant to a number of applications in modern commerce. Examples include panel sales data and data collected from web-commerce systems such as recommendation engines. An important unresolved question for this problem is characterizing the distribution of estimated matrix entries under common low-rank estimators. Such a characterization is essential to any application that requires quantification of uncertainty in these estimates and has heretofore only been available under the assumption of homogenous Gaussian noise. Here we characterize the distribution of estimated matrix entries when the observation noise is heterogeneous sub-exponential and provide, as an application, explicit formulas for this distribution when observed entries are Poisson or Binary distributed.

Learning Treatment Effects in Panels with General Intervention Patterns

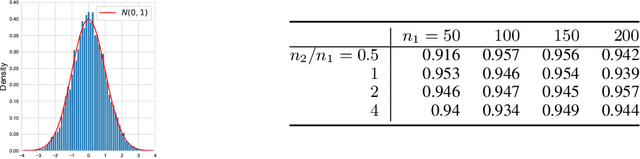
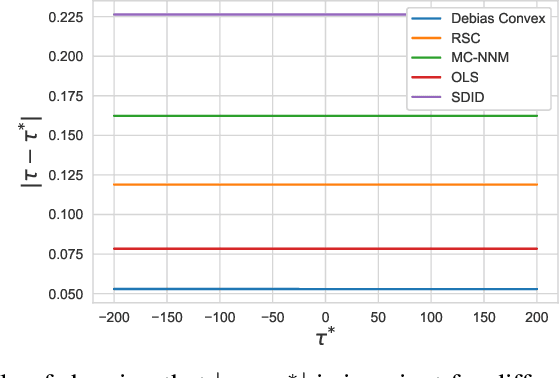
The problem of causal inference with panel data is a central econometric question. The following is a fundamental version of this problem: Let $M^*$ be a low rank matrix and $E$ be a zero-mean noise matrix. For a `treatment' matrix $Z$ with entries in $\{0,1\}$ we observe the matrix $O$ with entries $O_{ij} := M^*_{ij} + E_{ij} + \mathcal{T}_{ij} Z_{ij}$ where $\mathcal{T}_{ij} $ are unknown, heterogenous treatment effects. The problem requires we estimate the average treatment effect $\tau^* := \sum_{ij} \mathcal{T}_{ij} Z_{ij} / \sum_{ij} Z_{ij}$. The synthetic control paradigm provides an approach to estimating $\tau^*$ when $Z$ places support on a single row. This paper extends that framework to allow rate-optimal recovery of $\tau^*$ for general $Z$, thus broadly expanding its applicability. Our guarantees are the first of their type in this general setting. Computational experiments on synthetic and real-world data show a substantial advantage over competing estimators.

Fair Exploration via Axiomatic Bargaining

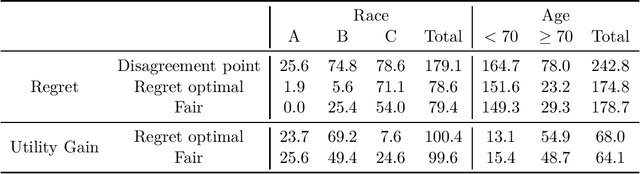
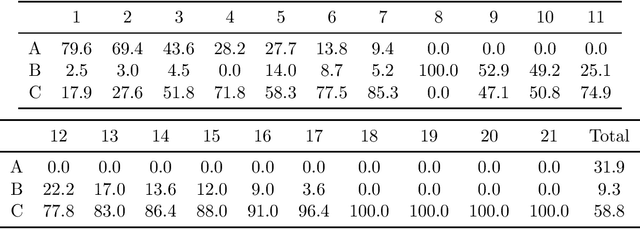
Motivated by the consideration of fairly sharing the cost of exploration between multiple groups in learning problems, we develop the Nash bargaining solution in the context of multi-armed bandits. Specifically, the 'grouped' bandit associated with any multi-armed bandit problem associates, with each time step, a single group from some finite set of groups. The utility gained by a given group under some learning policy is naturally viewed as the reduction in that group's regret relative to the regret that group would have incurred 'on its own'. We derive policies that yield the Nash bargaining solution relative to the set of incremental utilities possible under any policy. We show that on the one hand, the 'price of fairness' under such policies is limited, while on the other hand, regret optimal policies are arbitrarily unfair under generic conditions. Our theoretical development is complemented by a case study on contextual bandits for warfarin dosing where we are concerned with the cost of exploration across multiple races and age groups.

Optimizing Offer Sets in Sub-Linear Time

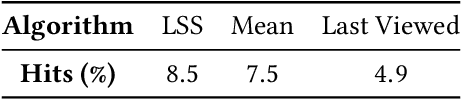
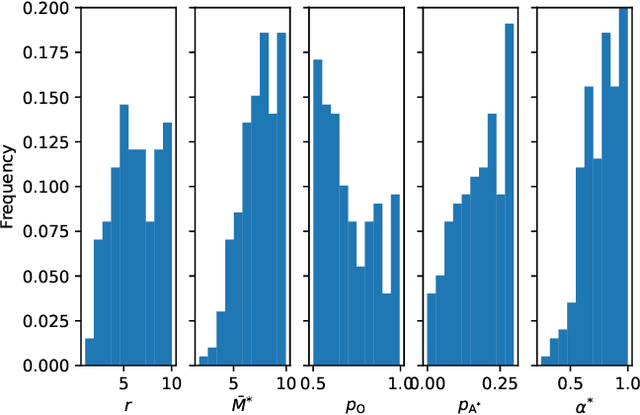
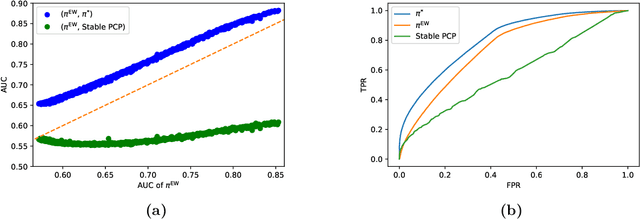
Personalization and recommendations are now accepted as core competencies in just about every online setting, ranging from media platforms to e-commerce to social networks. While the challenge of estimating user preferences has garnered significant attention, the operational problem of using such preferences to construct personalized offer sets to users is still a challenge, particularly in modern settings where a massive number of items and a millisecond response time requirement mean that even enumerating all of the items is impossible. Faced with such settings, existing techniques are either (a) entirely heuristic with no principled justification, or (b) theoretically sound, but simply too slow to work. Thus motivated, we propose an algorithm for personalized offer set optimization that runs in time sub-linear in the number of items while enjoying a uniform performance guarantee. Our algorithm works for an extremely general class of problems and models of user choice that includes the mixed multinomial logit model as a special case. We achieve a sub-linear runtime by leveraging the dimensionality reduction from learning an accurate latent factor model, along with existing sub-linear time approximate near neighbor algorithms. Our algorithm can be entirely data-driven, relying on samples of the user, where a `sample' refers to the user interaction data typically collected by firms. We evaluate our approach on a massive content discovery dataset from Outbrain that includes millions of advertisements. Results show that our implementation indeed runs fast and with increased performance relative to existing fast heuristics.

Solving the Phantom Inventory Problem: Near-optimal Entry-wise Anomaly Detection

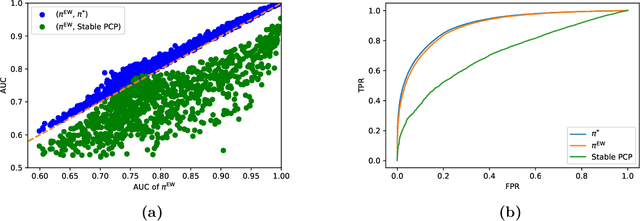
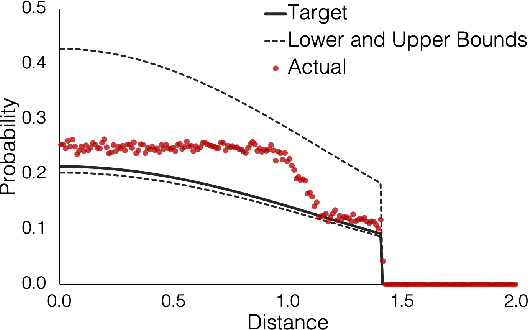
We observe that a crucial inventory management problem ('phantom inventory'), that by some measures costs retailers approximately 4% in annual sales can be viewed as a problem of identifying anomalies in a (low-rank) Poisson matrix. State of the art approaches to anomaly detection in low-rank matrices apparently fall short. Specifically, from a theoretical perspective, recovery guarantees for these approaches require that non-anomalous entries be observed with vanishingly small noise (which is not the case in our problem, and indeed in many applications). So motivated, we propose a conceptually simple entry-wise approach to anomaly detection in low-rank Poisson matrices. Our approach accommodates a general class of probabilistic anomaly models. We extend recent work on entry-wise error guarantees for matrix completion, establishing such guarantees for sub-exponential matrices, where in addition to missing entries, a fraction of entries are corrupted by (an also unknown) anomaly model. We show that for any given budget on the false positive rate (FPR), our approach achieves a true positive rate (TPR) that approaches the TPR of an (unachievable) optimal algorithm at a min-max optimal rate. Using data from a massive consumer goods retailer, we show that our approach provides significant improvements over incumbent approaches to anomaly detection.

The Limits to Learning an SIR Process: Granular Forecasting for Covid-19

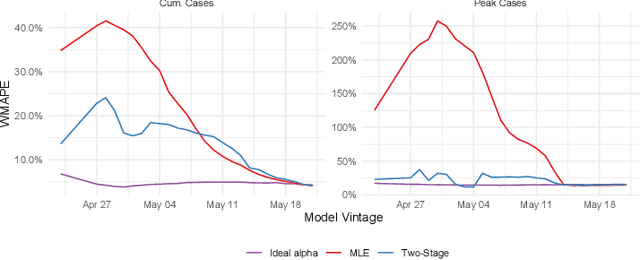
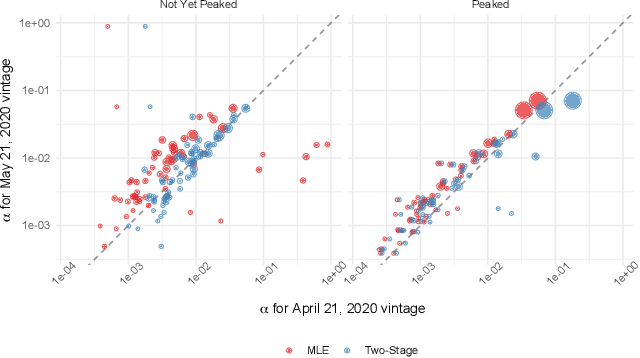
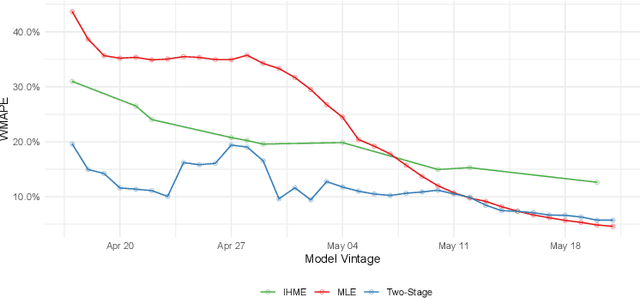
A multitude of forecasting efforts have arisen to support management of the ongoing COVID-19 epidemic. These efforts typically rely on a variant of the SIR process and have illustrated that building effective forecasts for an epidemic in its early stages is challenging. This is perhaps surprising since these models rely on a small number of parameters and typically provide an excellent retrospective fit to the evolution of a disease. So motivated, we provide an analysis of the limits to estimating an SIR process. We show that no unbiased estimator can hope to learn this process until observing enough of the epidemic so that one is approximately two-thirds of the way to reaching the peak for new infections. Our analysis provides insight into a regularization strategy that permits effective learning across simultaneously and asynchronously evolving epidemics. This strategy has been used to produce accurate, granular predictions for the COVID-19 epidemic that has found large-scale practical application in a large US state.