Solving the Phantom Inventory Problem: Near-optimal Entry-wise Anomaly Detection
Paper and Code
Jun 23, 2020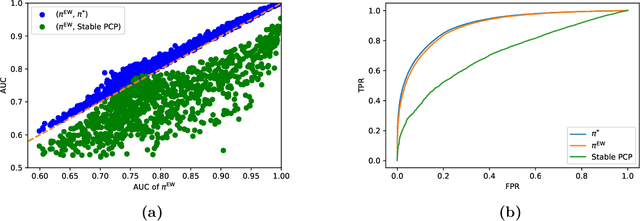
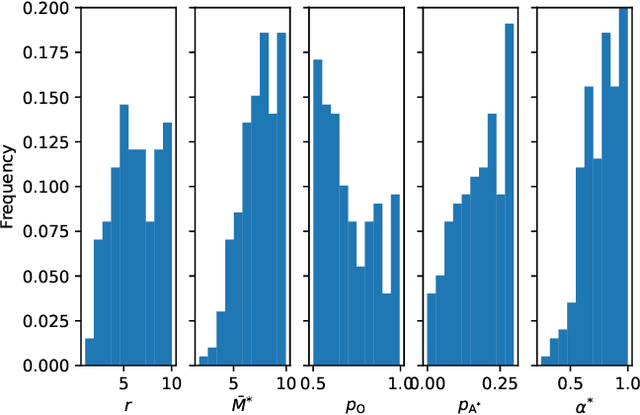
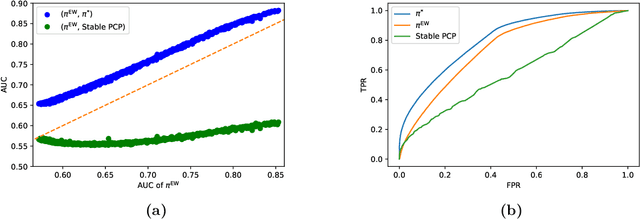
We observe that a crucial inventory management problem ('phantom inventory'), that by some measures costs retailers approximately 4% in annual sales can be viewed as a problem of identifying anomalies in a (low-rank) Poisson matrix. State of the art approaches to anomaly detection in low-rank matrices apparently fall short. Specifically, from a theoretical perspective, recovery guarantees for these approaches require that non-anomalous entries be observed with vanishingly small noise (which is not the case in our problem, and indeed in many applications). So motivated, we propose a conceptually simple entry-wise approach to anomaly detection in low-rank Poisson matrices. Our approach accommodates a general class of probabilistic anomaly models. We extend recent work on entry-wise error guarantees for matrix completion, establishing such guarantees for sub-exponential matrices, where in addition to missing entries, a fraction of entries are corrupted by (an also unknown) anomaly model. We show that for any given budget on the false positive rate (FPR), our approach achieves a true positive rate (TPR) that approaches the TPR of an (unachievable) optimal algorithm at a min-max optimal rate. Using data from a massive consumer goods retailer, we show that our approach provides significant improvements over incumbent approaches to anomaly detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge