Heterogeneous Treatment Effects in Panel Data

We address a core problem in causal inference: estimating heterogeneous treatment effects using panel data with general treatment patterns. Many existing methods either do not utilize the potential underlying structure in panel data or have limitations in the allowable treatment patterns. In this work, we propose and evaluate a new method that first partitions observations into disjoint clusters with similar treatment effects using a regression tree, and then leverages the (assumed) low-rank structure of the panel data to estimate the average treatment effect for each cluster. Our theoretical results establish the convergence of the resulting estimates to the true treatment effects. Computation experiments with semi-synthetic data show that our method achieves superior accuracy compared to alternative approaches, using a regression tree with no more than 40 leaves. Hence, our method provides more accurate and interpretable estimates than alternative methods.

The Limits to Learning an SIR Process: Granular Forecasting for Covid-19

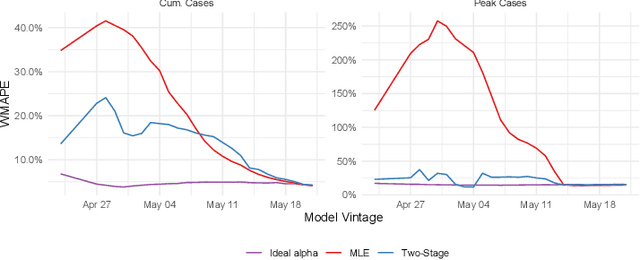
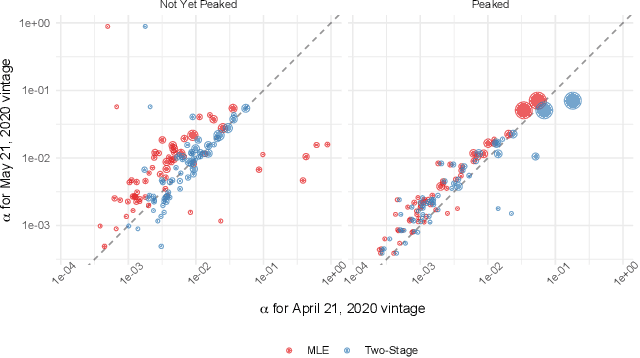
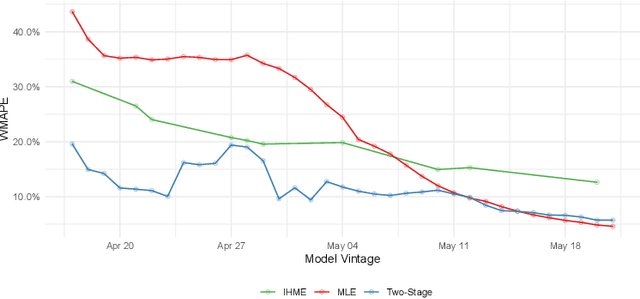
A multitude of forecasting efforts have arisen to support management of the ongoing COVID-19 epidemic. These efforts typically rely on a variant of the SIR process and have illustrated that building effective forecasts for an epidemic in its early stages is challenging. This is perhaps surprising since these models rely on a small number of parameters and typically provide an excellent retrospective fit to the evolution of a disease. So motivated, we provide an analysis of the limits to estimating an SIR process. We show that no unbiased estimator can hope to learn this process until observing enough of the epidemic so that one is approximately two-thirds of the way to reaching the peak for new infections. Our analysis provides insight into a regularization strategy that permits effective learning across simultaneously and asynchronously evolving epidemics. This strategy has been used to produce accurate, granular predictions for the COVID-19 epidemic that has found large-scale practical application in a large US state.