CoRe: Coherency Regularization for Hierarchical Time Series

Hierarchical time series forecasting presents unique challenges, particularly when dealing with noisy data that may not perfectly adhere to aggregation constraints. This paper introduces a novel approach to soft coherency in hierarchical time series forecasting using neural networks. We present a network coherency regularization method, which we denote as CoRe (Coherency Regularization), a technique that trains neural networks to produce forecasts that are inherently coherent across hierarchies, without strictly enforcing aggregation constraints. Our method offers several key advantages. (1) It provides theoretical guarantees on the coherency of forecasts, even for out-of-sample data. (2) It is adaptable to scenarios where data may contain errors or missing values, making it more robust than strict coherency methods. (3) It can be easily integrated into existing neural network architectures for time series forecasting. We demonstrate the effectiveness of our approach on multiple benchmark datasets, comparing it against state-of-the-art methods in both coherent and noisy data scenarios. Additionally, our method can be used within existing generative probabilistic forecasting frameworks to generate coherent probabilistic forecasts. Our results show improved generalization and forecast accuracy, particularly in the presence of data inconsistencies. On a variety of datasets, including both strictly hierarchically coherent and noisy data, our training method has either equal or better accuracy at all levels of the hierarchy while being strictly more coherent out-of-sample than existing soft-coherency methods.

Inter-Series Transformer: Attending to Products in Time Series Forecasting

Time series forecasting is an important task in many fields ranging from supply chain management to weather forecasting. Recently, Transformer neural network architectures have shown promising results in forecasting on common time series benchmark datasets. However, application to supply chain demand forecasting, which can have challenging characteristics such as sparsity and cross-series effects, has been limited. In this work, we explore the application of Transformer-based models to supply chain demand forecasting. In particular, we develop a new Transformer-based forecasting approach using a shared, multi-task per-time series network with an initial component applying attention across time series, to capture interactions and help address sparsity. We provide a case study applying our approach to successfully improve demand prediction for a medical device manufacturing company. To further validate our approach, we also apply it to public demand forecasting datasets as well and demonstrate competitive to superior performance compared to a variety of baseline and state-of-the-art forecast methods across the private and public datasets.

Heterogeneous Treatment Effects in Panel Data

We address a core problem in causal inference: estimating heterogeneous treatment effects using panel data with general treatment patterns. Many existing methods either do not utilize the potential underlying structure in panel data or have limitations in the allowable treatment patterns. In this work, we propose and evaluate a new method that first partitions observations into disjoint clusters with similar treatment effects using a regression tree, and then leverages the (assumed) low-rank structure of the panel data to estimate the average treatment effect for each cluster. Our theoretical results establish the convergence of the resulting estimates to the true treatment effects. Computation experiments with semi-synthetic data show that our method achieves superior accuracy compared to alternative approaches, using a regression tree with no more than 40 leaves. Hence, our method provides more accurate and interpretable estimates than alternative methods.

Tightness of prescriptive tree-based mixed-integer optimization formulations

We focus on modeling the relationship between an input feature vector and the predicted outcome of a trained decision tree using mixed-integer optimization. This can be used in many practical applications where a decision tree or tree ensemble is incorporated into an optimization problem to model the predicted outcomes of a decision. We propose tighter mixed-integer optimization formulations than those previously introduced. Existing formulations can be shown to have linear relaxations that have fractional extreme points, even for the simple case of modeling a single decision tree. A formulation we propose, based on a projected union of polyhedra approach, is ideal for a single decision tree. While the formulation is generally not ideal for tree ensembles or if additional constraints are added, it generally has fewer extreme points, leading to a faster time to solve, particularly if the formulation has relatively few trees. However, previous work has shown that formulations based on a binary representation of the feature vector perform well computationally and hence are attractive for use in practical applications. We present multiple approaches to tighten existing formulations with binary vectors, and show that fractional extreme points are removed when there are multiple splits on the same feature. At an extreme, we prove that this results in ideal formulations for tree ensembles modeling a one-dimensional feature vector. Building on this result, we also show via numerical simulations that these additional constraints result in significantly tighter linear relaxations when the feature vector is low dimensional. We also present instances where the time to solve to optimality is significantly improved using these formulations.

Optimizing Objective Functions from Trained ReLU Neural Networks via Sampling

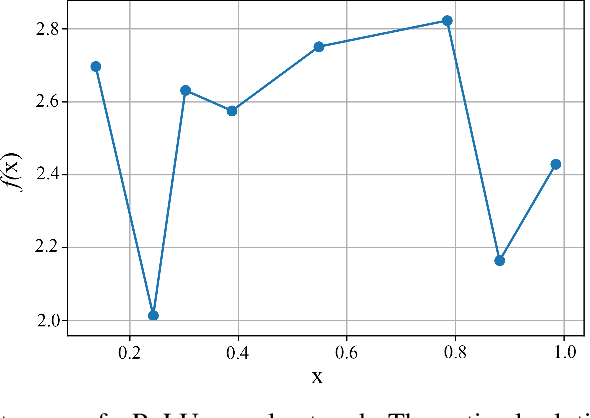
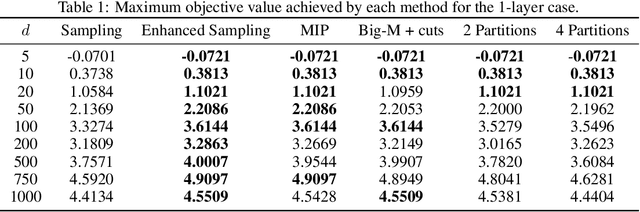
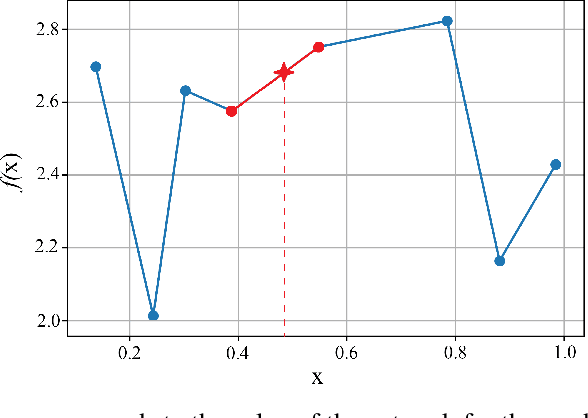
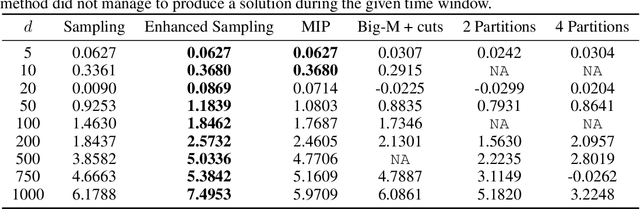
This paper introduces scalable, sampling-based algorithms that optimize trained neural networks with ReLU activations. We first propose an iterative algorithm that takes advantage of the piecewise linear structure of ReLU neural networks and reduces the initial mixed-integer optimization problem (MIP) into multiple easy-to-solve linear optimization problems (LPs) through sampling. Subsequently, we extend this approach by searching around the neighborhood of the LP solution computed at each iteration. This scheme allows us to devise a second, enhanced algorithm that reduces the initial MIP problem into smaller, easier-to-solve MIPs. We analytically show the convergence of the methods and we provide a sample complexity guarantee. We also validate the performance of our algorithms by comparing them against state-of-the-art MIP-based methods. Finally, we show computationally how the sampling algorithms can be used effectively to warm-start MIP-based methods.