Tightness of prescriptive tree-based mixed-integer optimization formulations

We focus on modeling the relationship between an input feature vector and the predicted outcome of a trained decision tree using mixed-integer optimization. This can be used in many practical applications where a decision tree or tree ensemble is incorporated into an optimization problem to model the predicted outcomes of a decision. We propose tighter mixed-integer optimization formulations than those previously introduced. Existing formulations can be shown to have linear relaxations that have fractional extreme points, even for the simple case of modeling a single decision tree. A formulation we propose, based on a projected union of polyhedra approach, is ideal for a single decision tree. While the formulation is generally not ideal for tree ensembles or if additional constraints are added, it generally has fewer extreme points, leading to a faster time to solve, particularly if the formulation has relatively few trees. However, previous work has shown that formulations based on a binary representation of the feature vector perform well computationally and hence are attractive for use in practical applications. We present multiple approaches to tighten existing formulations with binary vectors, and show that fractional extreme points are removed when there are multiple splits on the same feature. At an extreme, we prove that this results in ideal formulations for tree ensembles modeling a one-dimensional feature vector. Building on this result, we also show via numerical simulations that these additional constraints result in significantly tighter linear relaxations when the feature vector is low dimensional. We also present instances where the time to solve to optimality is significantly improved using these formulations.

Convex Loss Functions for Contextual Pricing with Observational Posted-Price Data

We study an off-policy contextual pricing problem where the seller has access to samples of prices which customers were previously offered, whether they purchased at that price, and auxiliary features describing the customer and/or item being sold. This is in contrast to the well-studied setting in which samples of the customer's valuation (willingness to pay) are observed. In our setting, the observed data is influenced by the historic pricing policy, and we do not know how customers would have responded to alternative prices. We introduce suitable loss functions for this pricing setting which can be directly optimized to find an effective pricing policy with expected revenue guarantees without the need for estimation of an intermediate demand function. We focus on convex loss functions. This is particularly relevant when linear pricing policies are desired for interpretability reasons, resulting in a tractable convex revenue optimization problem. We further propose generalized hinge and quantile pricing loss functions, which price at a multiplicative factor of the conditional expected value or a particular quantile of the valuation distribution when optimized, despite the valuation data not being observed. We prove expected revenue bounds for these pricing policies respectively when the valuation distribution is log-concave, and provide generalization bounds for the finite sample case. Finally, we conduct simulations on both synthetic and real-world data to demonstrate that this approach is competitive with, and in some settings outperforms, state-of-the-art methods in contextual pricing.

Enhancing Counterfactual Classification via Self-Training

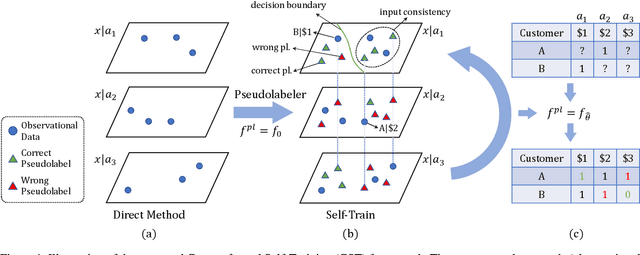
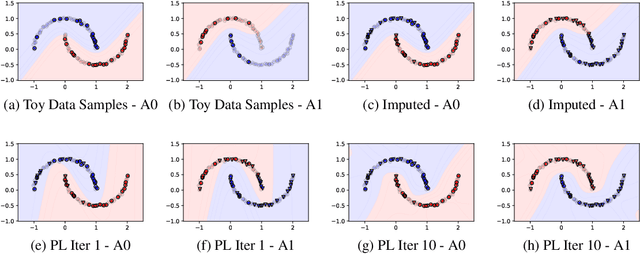
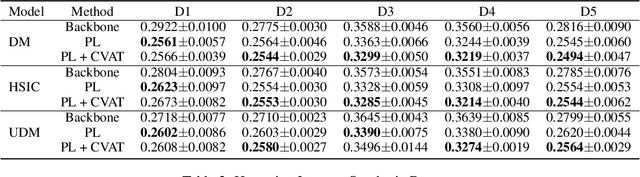
Unlike traditional supervised learning, in many settings only partial feedback is available. We may only observe outcomes for the chosen actions, but not the counterfactual outcomes associated with other alternatives. Such settings encompass a wide variety of applications including pricing, online marketing and precision medicine. A key challenge is that observational data are influenced by historical policies deployed in the system, yielding a biased data distribution. We approach this task as a domain adaptation problem and propose a self-training algorithm which imputes outcomes with categorical values for finite unseen actions in the observational data to simulate a randomized trial through pseudolabeling, which we refer to as Counterfactual Self-Training (CST). CST iteratively imputes pseudolabels and retrains the model. In addition, we show input consistency loss can further improve CST performance which is shown in recent theoretical analysis of pseudolabeling. We demonstrate the effectiveness of the proposed algorithms on both synthetic and real datasets.

Loss Functions for Discrete Contextual Pricing with Observational Data

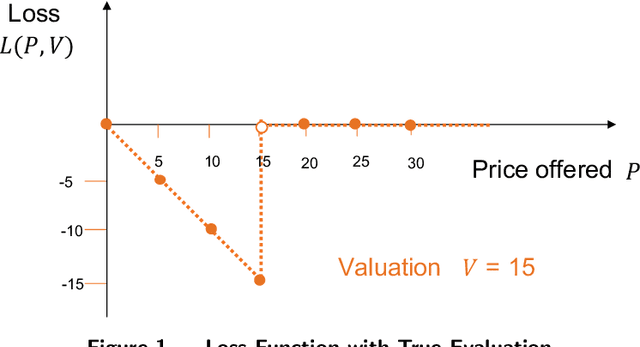
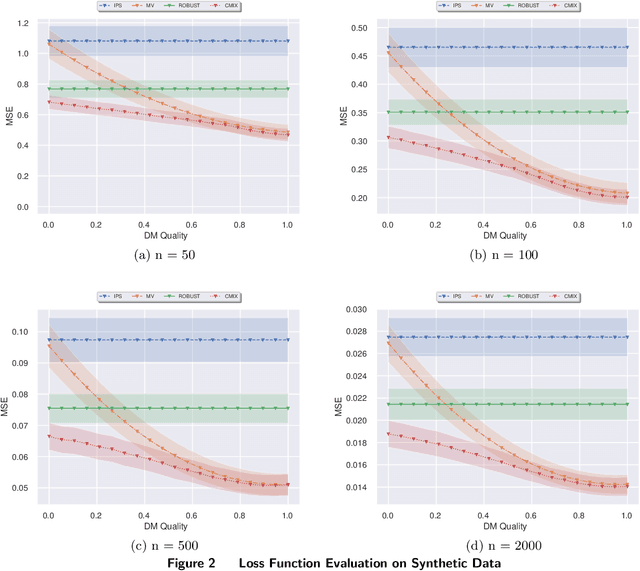
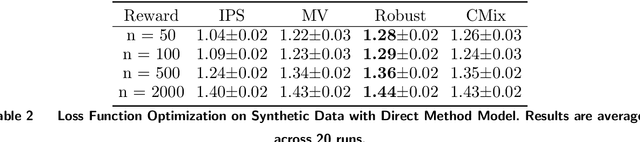
We study a pricing setting where each customer is offered a contextualized price based on customer and/or product features that are predictive of the customer's valuation for that product. Often only historical sales records are available, where we observe whether each customer purchased a product at the price prescribed rather than the customer's true valuation. As such, the data is influenced by the historical sales policy which introduces difficulties in a) estimating future loss/regret for pricing policies without the possibility of conducting real experiments and b) optimizing new policies for downstream tasks such as revenue management. We study how to formulate loss functions which can be used for optimizing pricing policies directly, rather than going through an intermediate demand estimation stage, which can be biased in practice due to model misspecification, regularization or poor calibration. While existing approaches have been proposed when valuation data is available, we propose loss functions for the observational data setting. To achieve this, we adapt ideas from machine learning with corrupted labels, where we can consider each observed customer's outcome (purchased or not for a prescribed price), as a (known) probabilistic transformation of the customer's valuation. From this transformation we derive a class of suitable unbiased loss functions. Within this class we identify minimum variance estimators, those which are robust to poor demand function estimation, and provide guidance on when the estimated demand function is useful. Furthermore, we also show that when applied to our contextual pricing setting, estimators popular in the off-policy evaluation literature fall within this class of loss functions, and also offer managerial insights on when each estimator is likely to perform well in practice.

Model Distillation for Revenue Optimization: Interpretable Personalized Pricing

Data-driven pricing strategies are becoming increasingly common, where customers are offered a personalized price based on features that are predictive of their valuation of a product. It is desirable to have this pricing policy be simple and interpretable, so it can be verified, checked for fairness, and easily implemented. However, efforts to incorporate machine learning into a pricing framework often lead to complex pricing policies which are not interpretable, resulting in mixed results in practice. We present a customized, prescriptive tree-based algorithm that distills knowledge from a complex black box machine learning algorithm, segments customers with similar valuations and prescribes prices in such a way that maximizes revenue while maintaining interpretability. We quantify the regret of a resulting policy and demonstrate its efficacy in applications with both synthetic and real-world datasets.