Loss Functions for Discrete Contextual Pricing with Observational Data
Paper and Code
Nov 18, 2021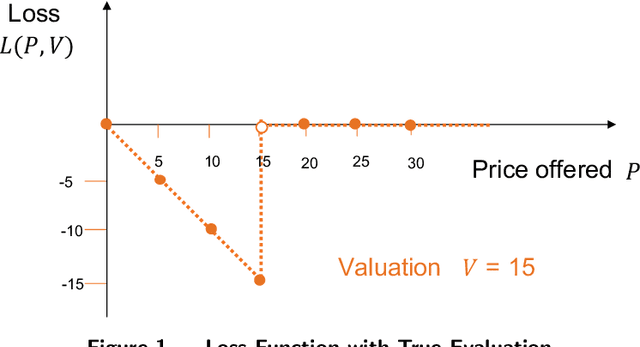

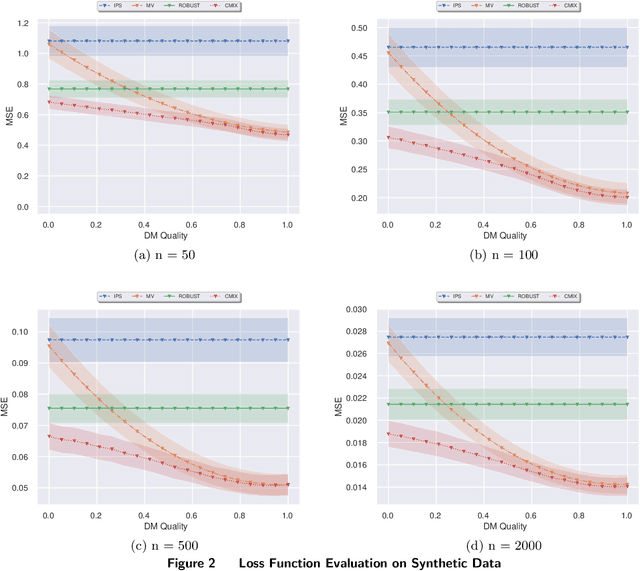
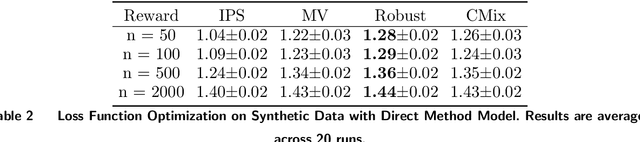
We study a pricing setting where each customer is offered a contextualized price based on customer and/or product features that are predictive of the customer's valuation for that product. Often only historical sales records are available, where we observe whether each customer purchased a product at the price prescribed rather than the customer's true valuation. As such, the data is influenced by the historical sales policy which introduces difficulties in a) estimating future loss/regret for pricing policies without the possibility of conducting real experiments and b) optimizing new policies for downstream tasks such as revenue management. We study how to formulate loss functions which can be used for optimizing pricing policies directly, rather than going through an intermediate demand estimation stage, which can be biased in practice due to model misspecification, regularization or poor calibration. While existing approaches have been proposed when valuation data is available, we propose loss functions for the observational data setting. To achieve this, we adapt ideas from machine learning with corrupted labels, where we can consider each observed customer's outcome (purchased or not for a prescribed price), as a (known) probabilistic transformation of the customer's valuation. From this transformation we derive a class of suitable unbiased loss functions. Within this class we identify minimum variance estimators, those which are robust to poor demand function estimation, and provide guidance on when the estimated demand function is useful. Furthermore, we also show that when applied to our contextual pricing setting, estimators popular in the off-policy evaluation literature fall within this class of loss functions, and also offer managerial insights on when each estimator is likely to perform well in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge