Causal LLM Routing: End-to-End Regret Minimization from Observational Data

LLM routing aims to select the most appropriate model for each query, balancing competing performance metrics such as accuracy and cost across a pool of language models. Prior approaches typically adopt a decoupled strategy, where the metrics are first predicted and the model is then selected based on these estimates. This setup is prone to compounding errors and often relies on full-feedback data, where each query is evaluated by all candidate models, which is costly to obtain and maintain in practice. In contrast, we learn from observational data, which records only the outcome of the model actually deployed. We propose a causal end-to-end framework that learns routing policies by minimizing decision-making regret from observational data. To enable efficient optimization, we introduce two theoretically grounded surrogate objectives: a classification-based upper bound, and a softmax-weighted regret approximation shown to recover the optimal policy at convergence. We further extend our framework to handle heterogeneous cost preferences via an interval-conditioned architecture. Experiments on public benchmarks show that our method outperforms existing baselines, achieving state-of-the-art performance across different embedding models.

Learning Prescriptive ReLU Networks

We study the problem of learning optimal policy from a set of discrete treatment options using observational data. We propose a piecewise linear neural network model that can balance strong prescriptive performance and interpretability, which we refer to as the prescriptive ReLU network, or P-ReLU. We show analytically that this model (i) partitions the input space into disjoint polyhedra, where all instances that belong to the same partition receive the same treatment, and (ii) can be converted into an equivalent prescriptive tree with hyperplane splits for interpretability. We demonstrate the flexibility of the P-ReLU network as constraints can be easily incorporated with minor modifications to the architecture. Through experiments, we validate the superior prescriptive accuracy of P-ReLU against competing benchmarks. Lastly, we present examples of interpretable prescriptive trees extracted from trained P-ReLUs using a real-world dataset, for both the unconstrained and constrained scenarios.

Optimizing Objective Functions from Trained ReLU Neural Networks via Sampling

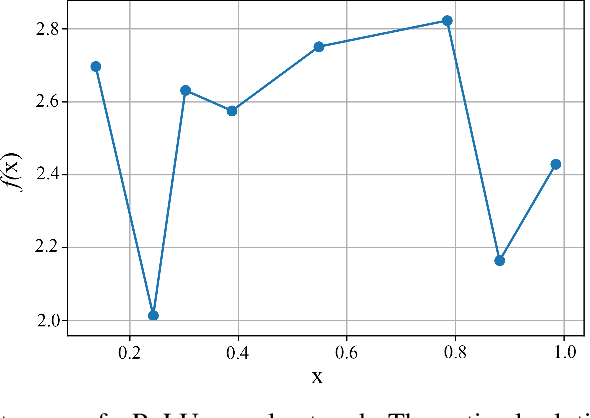
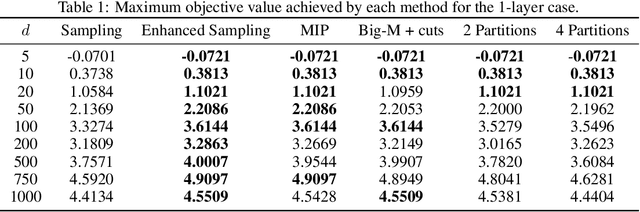
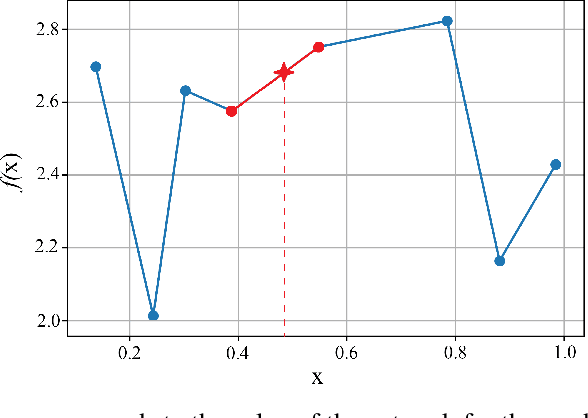
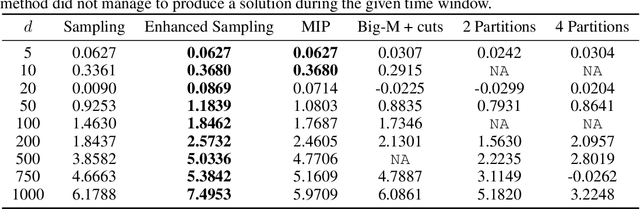
This paper introduces scalable, sampling-based algorithms that optimize trained neural networks with ReLU activations. We first propose an iterative algorithm that takes advantage of the piecewise linear structure of ReLU neural networks and reduces the initial mixed-integer optimization problem (MIP) into multiple easy-to-solve linear optimization problems (LPs) through sampling. Subsequently, we extend this approach by searching around the neighborhood of the LP solution computed at each iteration. This scheme allows us to devise a second, enhanced algorithm that reduces the initial MIP problem into smaller, easier-to-solve MIPs. We analytically show the convergence of the methods and we provide a sample complexity guarantee. We also validate the performance of our algorithms by comparing them against state-of-the-art MIP-based methods. Finally, we show computationally how the sampling algorithms can be used effectively to warm-start MIP-based methods.