Variational Weighting for Kernel Density Ratios
Paper and Code
Nov 06, 2023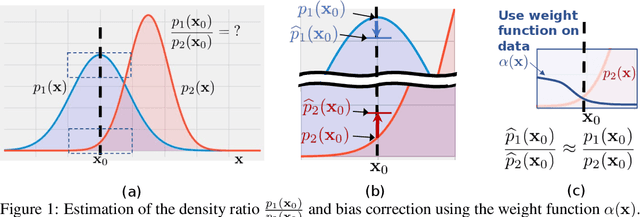
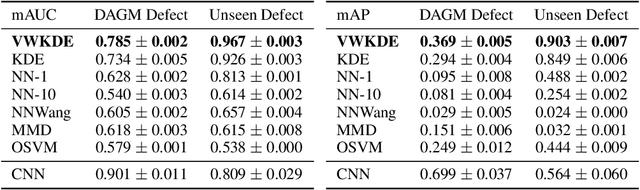
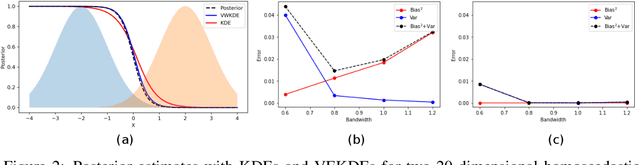

Kernel density estimation (KDE) is integral to a range of generative and discriminative tasks in machine learning. Drawing upon tools from the multidimensional calculus of variations, we derive an optimal weight function that reduces bias in standard kernel density estimates for density ratios, leading to improved estimates of prediction posteriors and information-theoretic measures. In the process, we shed light on some fundamental aspects of density estimation, particularly from the perspective of algorithms that employ KDEs as their main building blocks.
* NeurIPS 2023
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge