Deep $\mathcal{L}^1$ Stochastic Optimal Control Policies for Planetary Soft-landing

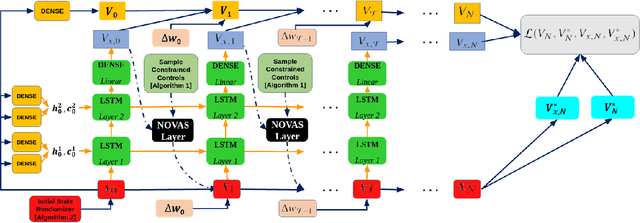
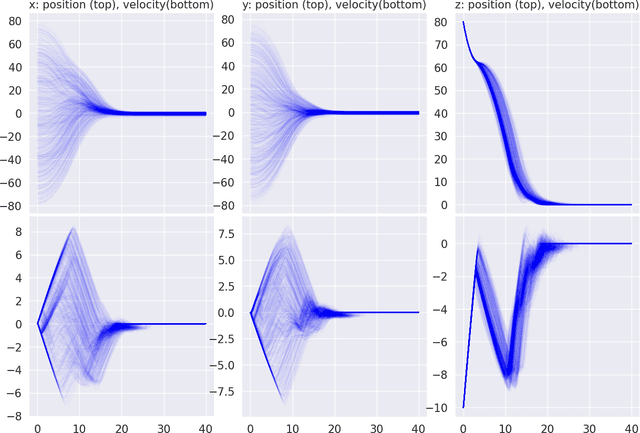
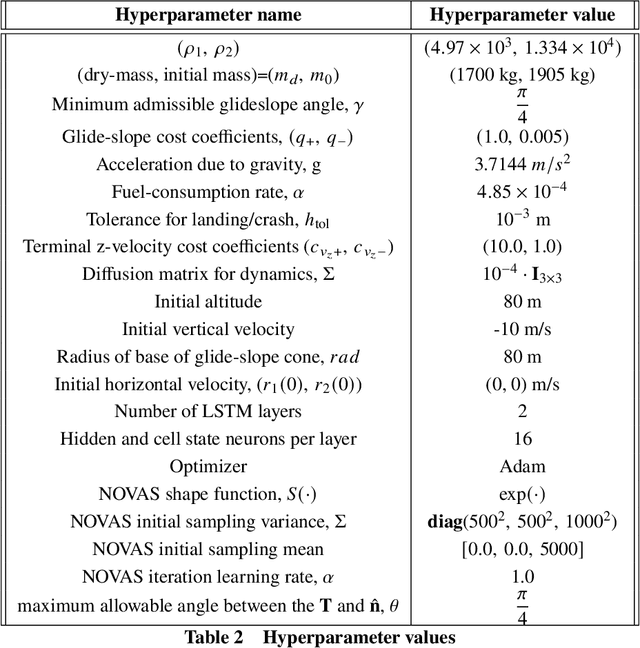
In this paper, we introduce a novel deep learning based solution to the Powered-Descent Guidance (PDG) problem, grounded in principles of nonlinear Stochastic Optimal Control (SOC) and Feynman-Kac theory. Our algorithm solves the PDG problem by framing it as an $\mathcal{L}^1$ SOC problem for minimum fuel consumption. Additionally, it can handle practically useful control constraints, nonlinear dynamics and enforces state constraints as soft-constraints. This is achieved by building off of recent work on deep Forward-Backward Stochastic Differential Equations (FBSDEs) and differentiable non-convex optimization neural-network layers based on stochastic search. In contrast to previous approaches, our algorithm does not require convexification of the constraints or linearization of the dynamics and is empirically shown to be robust to stochastic disturbances and the initial position of the spacecraft. After training offline, our controller can be activated once the spacecraft is within a pre-specified radius of the landing zone and at a pre-specified altitude i.e., the base of an inverted cone with the tip at the landing zone. We demonstrate empirically that our controller can successfully and safely land all trajectories initialized at the base of this cone while minimizing fuel consumption.

Adaptive CVaR Optimization for Dynamical Systems with Path Space Stochastic Search

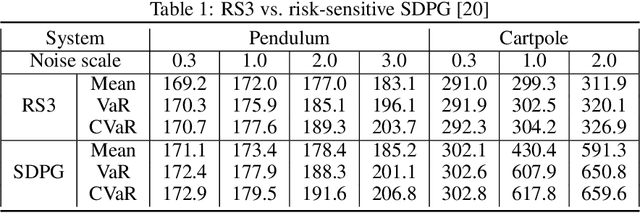
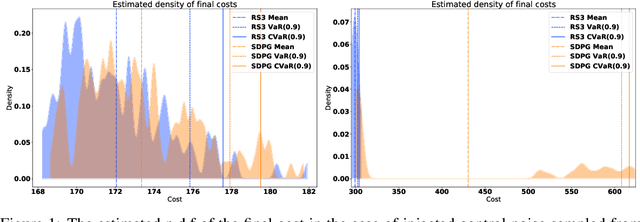
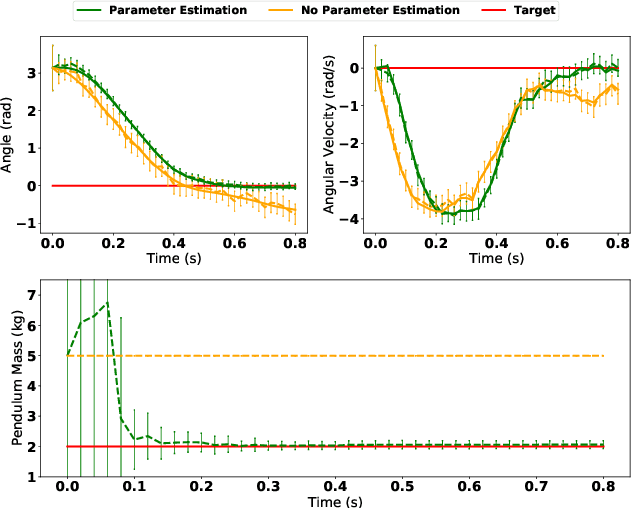
We present a general framework for optimizing the Conditional Value-at-Risk for dynamical systems using stochastic search. The framework is capable of handling the uncertainty from the initial condition, stochastic dynamics, and uncertain parameters in the model. The algorithm is compared against a risk-sensitive distributional reinforcement learning framework and demonstrates outperformance on a pendulum and cartpole with stochastic dynamics. We also showcase the applicability of the framework to robotics as an adaptive risk-sensitive controller by optimizing with respect to the fully nonlinear belief provided by a particle filter on a pendulum, cartpole, and quadcopter in simulation.