Decentralized Safe Multi-agent Stochastic Optimal Control using Deep FBSDEs and ADMM

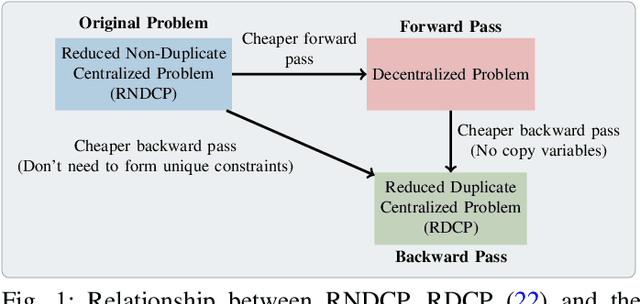
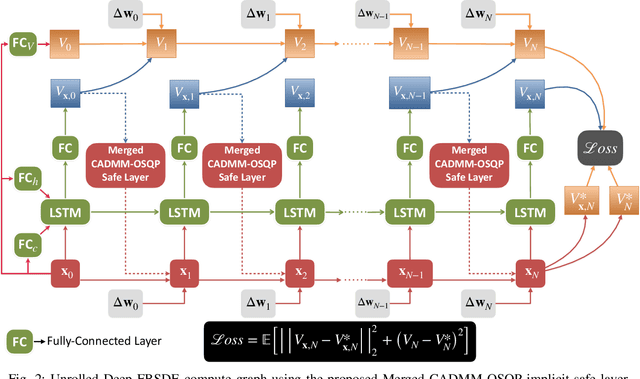
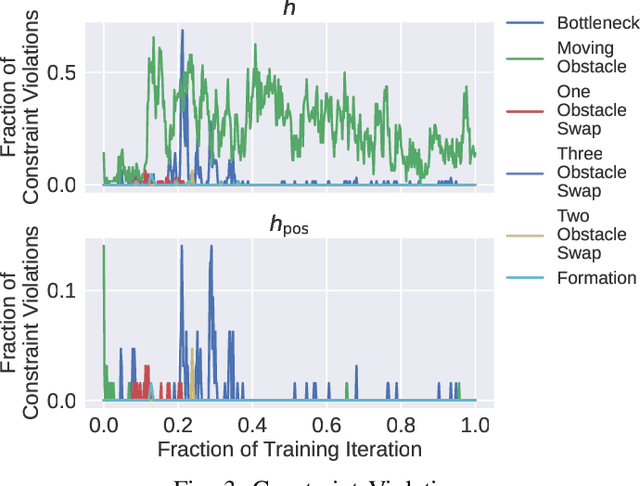
In this work, we propose a novel safe and scalable decentralized solution for multi-agent control in the presence of stochastic disturbances. Safety is mathematically encoded using stochastic control barrier functions and safe controls are computed by solving quadratic programs. Decentralization is achieved by augmenting to each agent's optimization variables, copy variables, for its neighbors. This allows us to decouple the centralized multi-agent optimization problem. However, to ensure safety, neighboring agents must agree on "what is safe for both of us" and this creates a need for consensus. To enable safe consensus solutions, we incorporate an ADMM-based approach. Specifically, we propose a Merged CADMM-OSQP implicit neural network layer, that solves a mini-batch of both, local quadratic programs as well as the overall consensus problem, as a single optimization problem. This layer is embedded within a Deep FBSDEs network architecture at every time step, to facilitate end-to-end differentiable, safe and decentralized stochastic optimal control. The efficacy of the proposed approach is demonstrated on several challenging multi-robot tasks in simulation. By imposing requirements on safety specified by collision avoidance constraints, the safe operation of all agents is ensured during the entire training process. We also demonstrate superior scalability in terms of computational and memory savings as compared to a centralized approach.

Deep $\mathcal{L}^1$ Stochastic Optimal Control Policies for Planetary Soft-landing

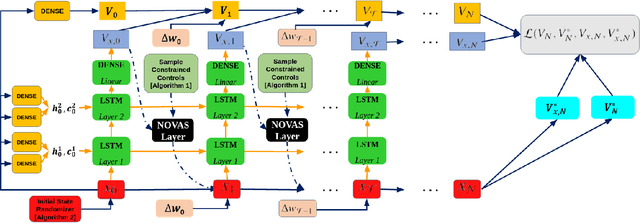
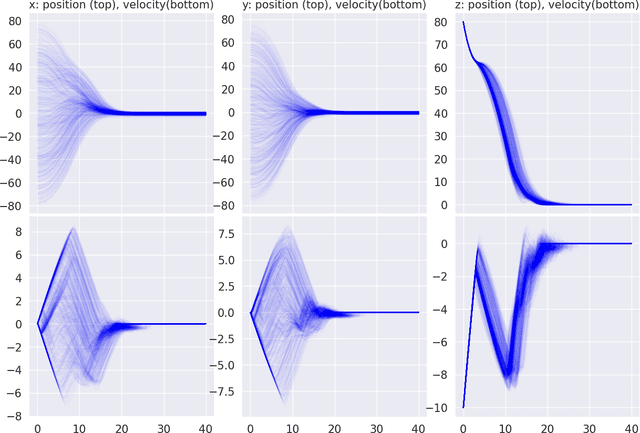
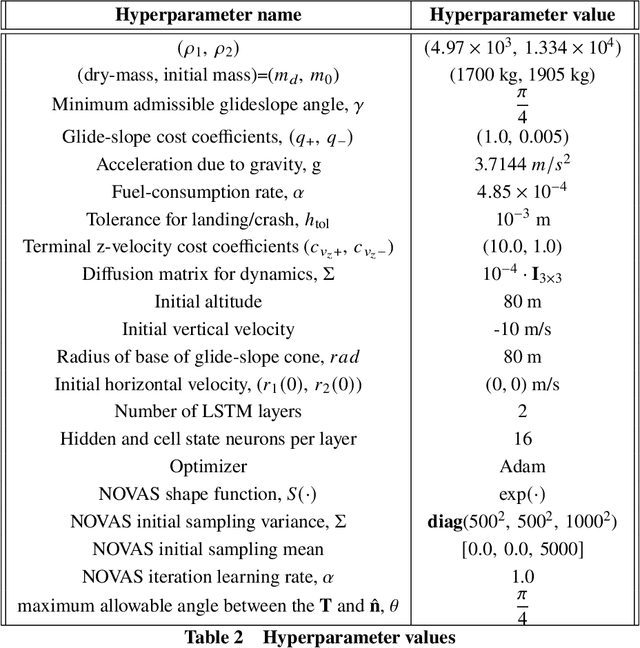
In this paper, we introduce a novel deep learning based solution to the Powered-Descent Guidance (PDG) problem, grounded in principles of nonlinear Stochastic Optimal Control (SOC) and Feynman-Kac theory. Our algorithm solves the PDG problem by framing it as an $\mathcal{L}^1$ SOC problem for minimum fuel consumption. Additionally, it can handle practically useful control constraints, nonlinear dynamics and enforces state constraints as soft-constraints. This is achieved by building off of recent work on deep Forward-Backward Stochastic Differential Equations (FBSDEs) and differentiable non-convex optimization neural-network layers based on stochastic search. In contrast to previous approaches, our algorithm does not require convexification of the constraints or linearization of the dynamics and is empirically shown to be robust to stochastic disturbances and the initial position of the spacecraft. After training offline, our controller can be activated once the spacecraft is within a pre-specified radius of the landing zone and at a pre-specified altitude i.e., the base of an inverted cone with the tip at the landing zone. We demonstrate empirically that our controller can successfully and safely land all trajectories initialized at the base of this cone while minimizing fuel consumption.

Non-convex Optimization via Adaptive Stochastic Search for End-to-End Learning and Control

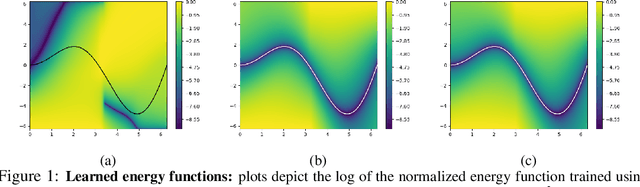
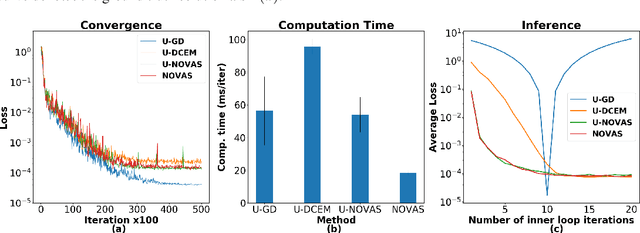
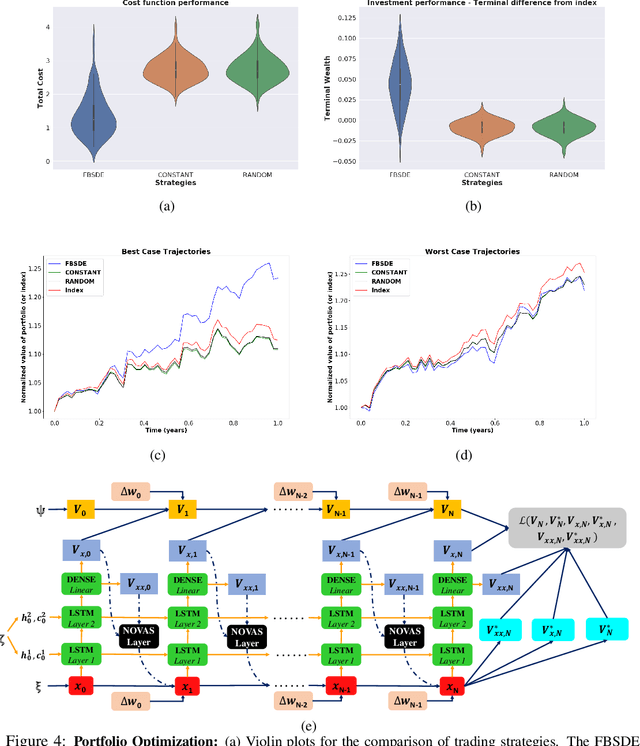
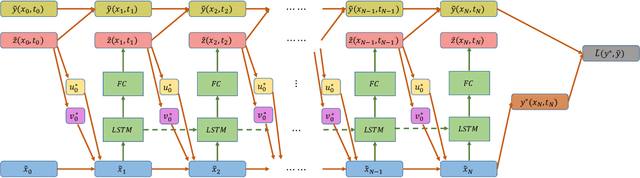
In this work we propose the use of adaptive stochastic search as a building block for general, non-convex optimization operations within deep neural network architectures. Specifically, for an objective function located at some layer in the network and parameterized by some network parameters, we employ adaptive stochastic search to perform optimization over its output. This operation is differentiable and does not obstruct the passing of gradients during backpropagation, thus enabling us to incorporate it as a component in end-to-end learning. We study the proposed optimization module's properties and benchmark it against two existing alternatives on a synthetic energy-based structured prediction task, and further showcase its use in stochastic optimal control applications.

Deep Forward-Backward SDEs for Min-max Control

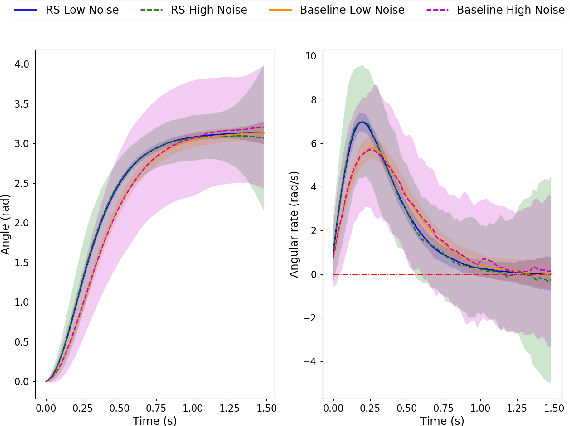
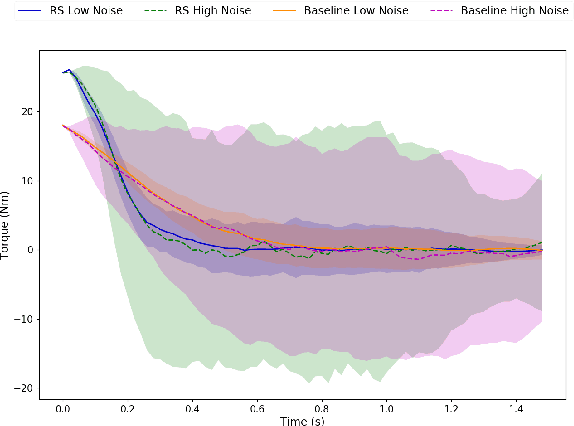
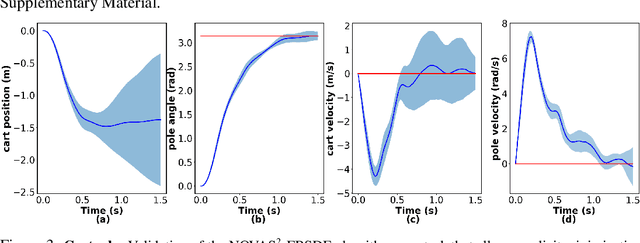
This paper presents a novel approach to numerically solve stochastic differential games for nonlinear systems. The proposed approach relies on the nonlinear Feynman-Kac theorem that establishes a connection between parabolic deterministic partial differential equations and forward-backward stochastic differential equations. Using this theorem the Hamilton-Jacobi-Isaacs partial differential equation associated with differential games is represented by a system of forward-backward stochastic differential equations. Numerical solution of the aforementioned system of stochastic differential equations is performed using importance sampling and a Long-Short Term Memory recurrent neural network, which is trained in an offline fashion. The resulting algorithm is tested on two example systems in simulation and compared against the standard risk neutral stochastic optimal control formulations.

Deep 2FBSDEs for Systems with Control Multiplicative Noise

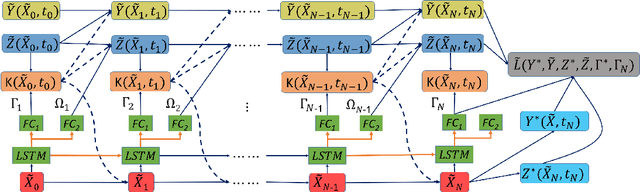
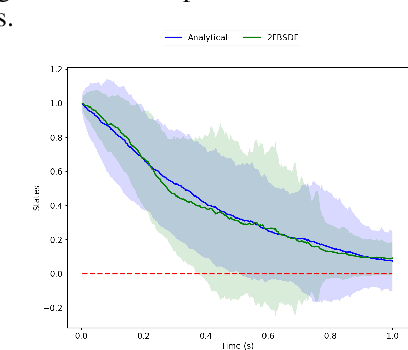
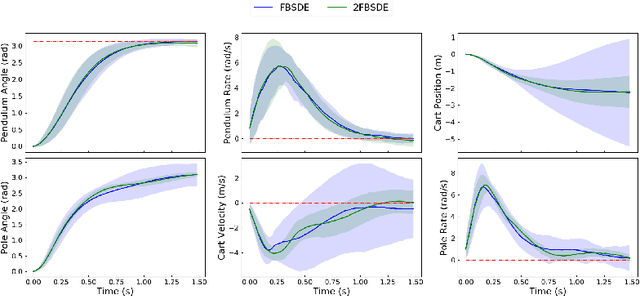
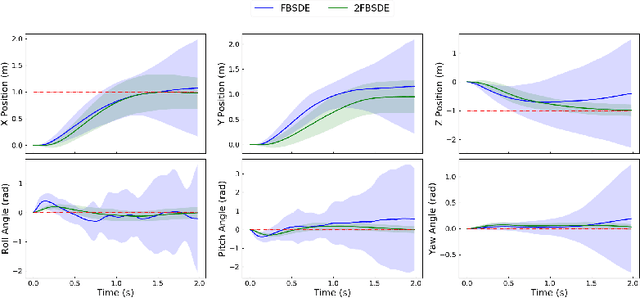
We present a deep recurrent neural network architecture to solve a class of stochastic optimal control problems described by fully nonlinear Hamilton Jacobi Bellman partial differential equations. Such PDEs arise when one considers stochastic dynamics characterized by uncertainties that are additive and control multiplicative. Stochastic models with the aforementioned characteristics have been used in computational neuroscience, biology and aerospace systems and provide a more accurate representation of actuation than models with additive uncertainty. Previous literature has established the inadequacy of the linear HJB theory and and instead rely on a non-linear Feynman-Kac lemma resulting in a second order forward-backward stochastic differential equations representation. However, the proposed solutions that use this representation suffer from compounding errors and computational complexity leading to lack of scalability. In this paper, we propose a deep learning based algorithm that leverages the second order Forward-Bacward SDE representation along with importance sampling and LSTM based recurrent neural networks to not only solve such Stochastic Optimal Control problems but also overcome the problems faced by previous approaches and scales well to high dimensional systems. The resulting control algorithm is tested on three non-linear systems to demonstrate feasibility and out-performance against previous methods.