Adaptive CVaR Optimization for Dynamical Systems with Path Space Stochastic Search
Paper and Code
Sep 02, 2020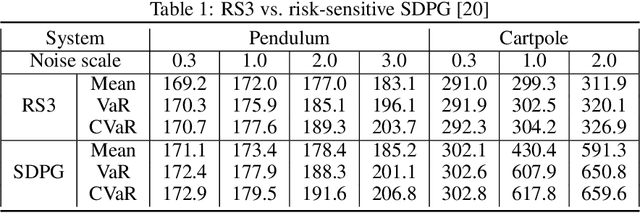
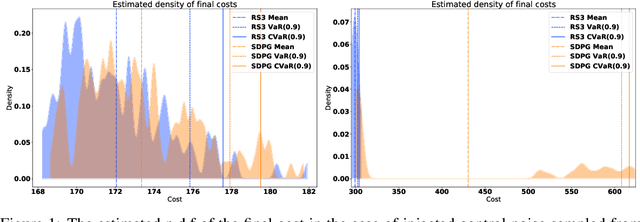
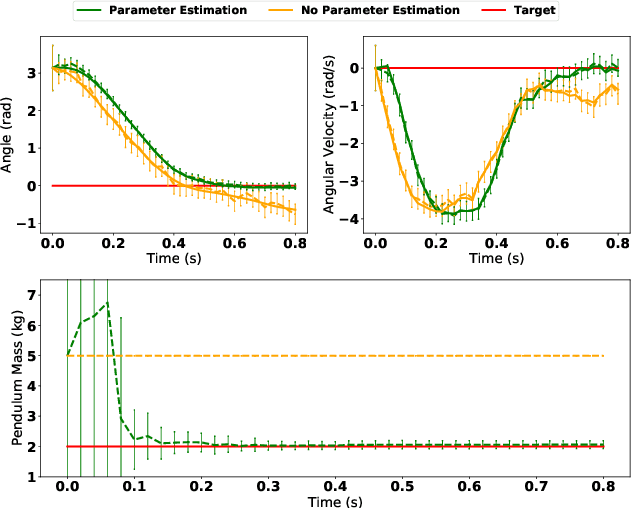

We present a general framework for optimizing the Conditional Value-at-Risk for dynamical systems using stochastic search. The framework is capable of handling the uncertainty from the initial condition, stochastic dynamics, and uncertain parameters in the model. The algorithm is compared against a risk-sensitive distributional reinforcement learning framework and demonstrates outperformance on a pendulum and cartpole with stochastic dynamics. We also showcase the applicability of the framework to robotics as an adaptive risk-sensitive controller by optimizing with respect to the fully nonlinear belief provided by a particle filter on a pendulum, cartpole, and quadcopter in simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge