Neural Network Architectures for Stochastic Control using the Nonlinear Feynman-Kac Lemma

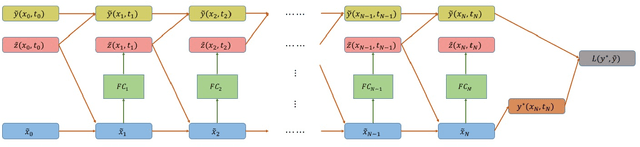
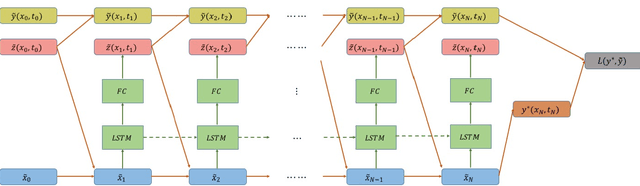
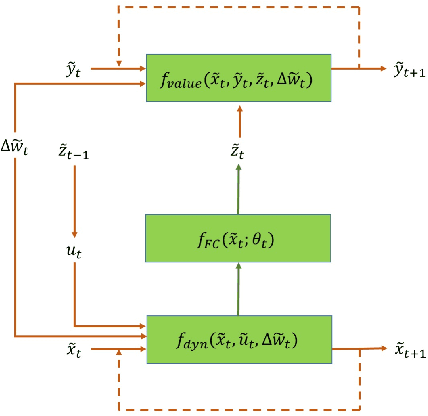
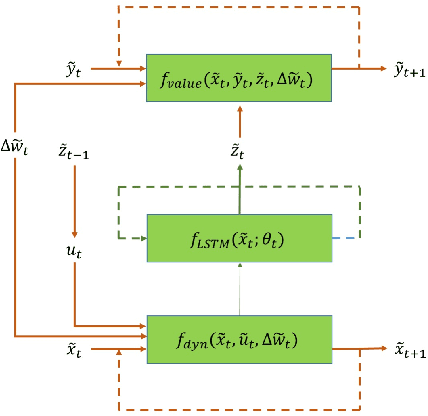
In this paper we propose a new methodology for decision-making under uncertainty using recent advancements in the areas of nonlinear stochastic optimal control theory, applied mathematics and machine learning. Our work is grounded on the nonlinear Feynman-Kac lemma and the fundamental connection between backward nonlinear partial differential equations and forward-backward stochastic differential equations. Using these connections and results from our prior work on importance sampling for forward-backward stochastic differential equations, we develop a control framework that is scalable and applicable to general classes of stochastic systems and decision-making problem formulations in robotics and autonomy. Two architectures for stochastic control are proposed that consist of feed-forward and recurrent neural networks. The performance and scalability of the aforementioned algorithms is investigated in two stochastic optimal control problem formulations including the unconstrained L2 and control-constrained case, and three systems in simulation. We conclude with a discussion on the implications of the proposed algorithms to robotics and autonomous systems.