Newton Meets Marchenko-Pastur: Massively Parallel Second-Order Optimization with Hessian Sketching and Debiasing

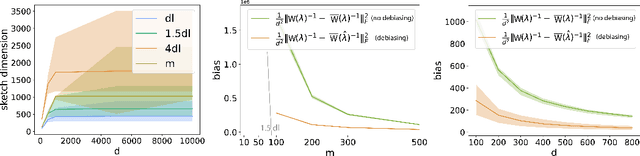
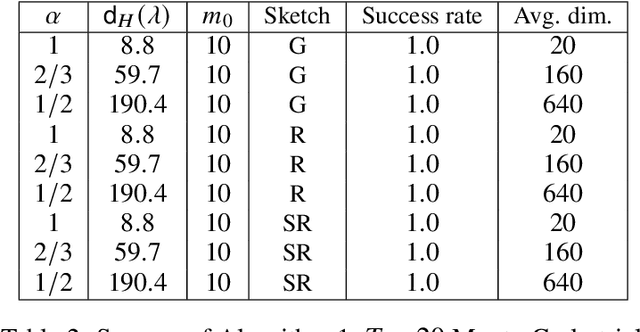
Motivated by recent advances in serverless cloud computing, in particular the "function as a service" (FaaS) model, we consider the problem of minimizing a convex function in a massively parallel fashion, where communication between workers is limited. Focusing on the case of a twice-differentiable objective subject to an L2 penalty, we propose a scheme where the central node (server) effectively runs a Newton method, offloading its high per-iteration cost -- stemming from the need to invert the Hessian -- to the workers. In our solution, workers produce independently coarse but low-bias estimates of the inverse Hessian, using an adaptive sketching scheme. The server then averages the descent directions produced by the workers, yielding a good approximation for the exact Newton step. The main component of our adaptive sketching scheme is a low-complexity procedure for selecting the sketching dimension, an issue that was left largely unaddressed in the existing literature on Hessian sketching for distributed optimization. Our solution is based on ideas from asymptotic random matrix theory, specifically the Marchenko-Pastur law. For Gaussian sketching matrices, we derive non asymptotic guarantees for our algorithm which are essentially dimension-free. Lastly, when the objective is self-concordant, we provide convergence guarantees for the approximate Newton's method with noisy Hessians, which may be of independent interest beyond the setting considered in this paper.

On the Noise Sensitivity of the Randomized SVD

The randomized singular value decomposition (R-SVD) is a popular sketching-based algorithm for efficiently computing the partial SVD of a large matrix. When the matrix is low-rank, the R-SVD produces its partial SVD exactly; but when the rank is large, it only yields an approximation. Motivated by applications in data science and principal component analysis (PCA), we analyze the R-SVD under a low-rank signal plus noise measurement model; specifically, when its input is a spiked random matrix. The singular values produced by the R-SVD are shown to exhibit a BBP-like phase transition: when the SNR exceeds a certain detectability threshold, that depends on the dimension reduction factor, the largest singular value is an outlier; below the threshold, no outlier emerges from the bulk of singular values. We further compute asymptotic formulas for the overlap between the ground truth signal singular vectors and the approximations produced by the R-SVD. Dimensionality reduction has the adverse affect of amplifying the noise in a highly nonlinear manner. Our results demonstrate the statistical advantage -- in both signal detection and estimation -- of the R-SVD over more naive sketched PCA variants; the advantage is especially dramatic when the sketching dimension is small. Our analysis is asymptotically exact, and substantially more fine-grained than existing operator-norm error bounds for the R-SVD, which largely fail to give meaningful error estimates in the moderate SNR regime. It applies for a broad family of sketching matrices previously considered in the literature, including Gaussian i.i.d. sketches, random projections, and the sub-sampled Hadamard transform, among others. Lastly, we derive an optimal singular value shrinker for singular values and vectors obtained through the R-SVD, which may be useful for applications in matrix denoising.

Matrix Denoising with Partial Noise Statistics: Optimal Singular Value Shrinkage of Spiked F-Matrices

We study the problem of estimating a large, low-rank matrix corrupted by additive noise of unknown covariance, assuming one has access to additional side information in the form of noise-only measurements. We study the Whiten-Shrink-reColor (WSC) workflow, where a "noise covariance whitening" transformation is applied to the observations, followed by appropriate singular value shrinkage and a "noise covariance re-coloring" transformation. We show that under the mean square error loss, a unique, asymptotically optimal shrinkage nonlinearity exists for the WSC denoising workflow, and calculate it in closed form. To this end, we calculate the asymptotic eigenvector rotation of the random spiked F-matrix ensemble, a result which may be of independent interest. With sufficiently many pure-noise measurements, our optimally-tuned WSC denoising workflow outperforms, in mean square error, matrix denoising algorithms based on optimal singular value shrinkage which do not make similar use of noise-only side information; numerical experiments show that our procedure's relative performance is particularly strong in challenging statistical settings with high dimensionality and large degree of heteroscedasticity.

On the Role of Channel Capacity in Learning Gaussian Mixture Models

This paper studies the sample complexity of learning the $k$ unknown centers of a balanced Gaussian mixture model (GMM) in $\mathbb{R}^d$ with spherical covariance matrix $\sigma^2\mathbf{I}$. In particular, we are interested in the following question: what is the maximal noise level $\sigma^2$, for which the sample complexity is essentially the same as when estimating the centers from labeled measurements? To that end, we restrict attention to a Bayesian formulation of the problem, where the centers are uniformly distributed on the sphere $\sqrt{d}\mathcal{S}^{d-1}$. Our main results characterize the exact noise threshold $\sigma^2$ below which the GMM learning problem, in the large system limit $d,k\to\infty$, is as easy as learning from labeled observations, and above which it is substantially harder. The threshold occurs at $\frac{\log k}{d} = \frac12\log\left( 1+\frac{1}{\sigma^2} \right)$, which is the capacity of the additive white Gaussian noise (AWGN) channel. Thinking of the set of $k$ centers as a code, this noise threshold can be interpreted as the largest noise level for which the error probability of the code over the AWGN channel is small. Previous works on the GMM learning problem have identified the minimum distance between the centers as a key parameter in determining the statistical difficulty of learning the corresponding GMM. While our results are only proved for GMMs whose centers are uniformly distributed over the sphere, they hint that perhaps it is the decoding error probability associated with the center constellation as a channel code that determines the statistical difficulty of learning the corresponding GMM, rather than just the minimum distance.

Spiked Covariance Estimation from Modulo-Reduced Measurements

Consider the rank-1 spiked model: $\bf{X}=\sqrt{\nu}\xi \bf{u}+ \bf{Z}$, where $\nu$ is the spike intensity, $\bf{u}\in\mathbb{S}^{k-1}$ is an unknown direction and $\xi\sim \mathcal{N}(0,1),\bf{Z}\sim \mathcal{N}(\bf{0},\bf{I})$. Motivated by recent advances in analog-to-digital conversion, we study the problem of recovering $\bf{u}\in \mathbb{S}^{k-1}$ from $n$ i.i.d. modulo-reduced measurements $\bf{Y}=[\bf{X}]\mod \Delta$, focusing on the high-dimensional regime ($k\gg 1$). We develop and analyze an algorithm that, for most directions $\bf{u}$ and $\nu=\mathrm{poly}(k)$, estimates $\bf{u}$ to high accuracy using $n=\mathrm{poly}(k)$ measurements, provided that $\Delta\gtrsim \sqrt{\log k}$. Up to constants, our algorithm accurately estimates $\bf{u}$ at the smallest possible $\Delta$ that allows (in an information-theoretic sense) to recover $\bf{X}$ from $\bf{Y}$. A key step in our analysis involves estimating the probability that a line segment of length $\approx\sqrt{\nu}$ in a random direction $\bf{u}$ passes near a point in the lattice $\Delta \mathbb{Z}^k$. Numerical experiments show that the developed algorithm performs well even in a non-asymptotic setting.

On Compressed Sensing of Binary Signals for the Unsourced Random Access Channel

Motivated by applications in unsourced random access, this paper develops a novel scheme for the problem of compressed sensing of binary signals. In this problem, the goal is to design a sensing matrix $A$ and a recovery algorithm, such that the sparse binary vector $\mathbf{x}$ can be recovered reliably from the measurements $\mathbf{y}=A\mathbf{x}+\sigma\mathbf{z}$, where $\mathbf{z}$ is additive white Gaussian noise. We propose to design $A$ as a parity check matrix of a low-density parity-check code (LDPC), and to recover $\mathbf{x}$ from the measurements $\mathbf{y}$ using a Markov chain Monte Carlo algorithm, which runs relatively fast due to the sparse structure of $A$. The performance of our scheme is comparable to state-of-the-art schemes, which use dense sensing matrices, while enjoying the advantages of using a sparse sensing matrix.

Multi-reference alignment in high dimensions: sample complexity and phase transition

Multi-reference alignment entails estimating a signal in $\mathbb{R}^L$ from its circularly-shifted and noisy copies. This problem has been studied thoroughly in recent years, focusing on the finite-dimensional setting (fixed $L$). Motivated by single-particle cryo-electron microscopy, we analyze the sample complexity of the problem in the high-dimensional regime $L\to\infty$. Our analysis uncovers a phase transition phenomenon governed by the parameter $\alpha = L/(\sigma^2\log L)$, where $\sigma^2$ is the variance of the noise. When $\alpha>2$, the impact of the unknown circular shifts on the sample complexity is minor. Namely, the number of measurements required to achieve a desired accuracy $\varepsilon$ approaches $\sigma^2/\varepsilon$ for small $\varepsilon$; this is the sample complexity of estimating a signal in additive white Gaussian noise, which does not involve shifts. In sharp contrast, when $\alpha\leq 2$, the problem is significantly harder and the sample complexity grows substantially quicker with $\sigma^2$.