Active Learning of Deep Neural Networks via Gradient-Free Cutting Planes

Active learning methods aim to improve sample complexity in machine learning. In this work, we investigate an active learning scheme via a novel gradient-free cutting-plane training method for ReLU networks of arbitrary depth. We demonstrate, for the first time, that cutting-plane algorithms, traditionally used in linear models, can be extended to deep neural networks despite their nonconvexity and nonlinear decision boundaries. Our results demonstrate that these methods provide a promising alternative to the commonly employed gradient-based optimization techniques in large-scale neural networks. Moreover, this training method induces the first deep active learning scheme known to achieve convergence guarantees. We exemplify the effectiveness of our proposed active learning method against popular deep active learning baselines via both synthetic data experiments and sentimental classification task on real datasets.

Newton Meets Marchenko-Pastur: Massively Parallel Second-Order Optimization with Hessian Sketching and Debiasing

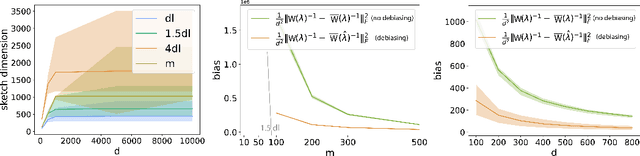
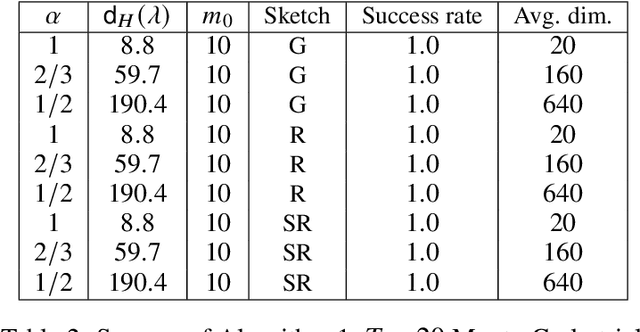
Motivated by recent advances in serverless cloud computing, in particular the "function as a service" (FaaS) model, we consider the problem of minimizing a convex function in a massively parallel fashion, where communication between workers is limited. Focusing on the case of a twice-differentiable objective subject to an L2 penalty, we propose a scheme where the central node (server) effectively runs a Newton method, offloading its high per-iteration cost -- stemming from the need to invert the Hessian -- to the workers. In our solution, workers produce independently coarse but low-bias estimates of the inverse Hessian, using an adaptive sketching scheme. The server then averages the descent directions produced by the workers, yielding a good approximation for the exact Newton step. The main component of our adaptive sketching scheme is a low-complexity procedure for selecting the sketching dimension, an issue that was left largely unaddressed in the existing literature on Hessian sketching for distributed optimization. Our solution is based on ideas from asymptotic random matrix theory, specifically the Marchenko-Pastur law. For Gaussian sketching matrices, we derive non asymptotic guarantees for our algorithm which are essentially dimension-free. Lastly, when the objective is self-concordant, we provide convergence guarantees for the approximate Newton's method with noisy Hessians, which may be of independent interest beyond the setting considered in this paper.

Spectral Adapter: Fine-Tuning in Spectral Space

Recent developments in Parameter-Efficient Fine-Tuning (PEFT) methods for pretrained deep neural networks have captured widespread interest. In this work, we study the enhancement of current PEFT methods by incorporating the spectral information of pretrained weight matrices into the fine-tuning procedure. We investigate two spectral adaptation mechanisms, namely additive tuning and orthogonal rotation of the top singular vectors, both are done via first carrying out Singular Value Decomposition (SVD) of pretrained weights and then fine-tuning the top spectral space. We provide a theoretical analysis of spectral fine-tuning and show that our approach improves the rank capacity of low-rank adapters given a fixed trainable parameter budget. We show through extensive experiments that the proposed fine-tuning model enables better parameter efficiency and tuning performance as well as benefits multi-adapter fusion. The code will be open-sourced for reproducibility.

Riemannian Preconditioned LoRA for Fine-Tuning Foundation Models

In this work we study the enhancement of Low Rank Adaptation (LoRA) fine-tuning procedure by introducing a Riemannian preconditioner in its optimization step. Specifically, we introduce an $r\times r$ preconditioner in each gradient step where $r$ is the LoRA rank. This preconditioner requires a small change to existing optimizer code and creates virtually minuscule storage and runtime overhead. Our experimental results with both large language models and text-to-image diffusion models show that with our preconditioner, the convergence and reliability of SGD and AdamW can be significantly enhanced. Moreover, the training process becomes much more robust to hyperparameter choices such as learning rate. Theoretically, we show that fine-tuning a two-layer ReLU network in the convex paramaterization with our preconditioner has convergence rate independent of condition number of the data matrix. This new Riemannian preconditioner, previously explored in classic low-rank matrix recovery, is introduced to deep learning tasks for the first time in our work. We release our code at https://github.com/pilancilab/Riemannian_Preconditioned_LoRA.

Analyzing Neural Network-Based Generative Diffusion Models through Convex Optimization

Diffusion models are becoming widely used in state-of-the-art image, video and audio generation. Score-based diffusion models stand out among these methods, necessitating the estimation of score function of the input data distribution. In this study, we present a theoretical framework to analyze two-layer neural network-based diffusion models by reframing score matching and denoising score matching as convex optimization. Though existing diffusion theory is mainly asymptotic, we characterize the exact predicted score function and establish the convergence result for neural network-based diffusion models with finite data. This work contributes to understanding what neural network-based diffusion model learns in non-asymptotic settings.