Preconditioned Subspace Langevin Monte Carlo

We develop a new efficient method for high-dimensional sampling called Subspace Langevin Monte Carlo. The primary application of these methods is to efficiently implement Preconditioned Langevin Monte Carlo. To demonstrate the usefulness of this new method, we extend ideas from subspace descent methods in Euclidean space to solving a specific optimization problem over Wasserstein space. Our theoretical analysis demonstrates the advantageous convergence regimes of the proposed method, which depend on relative conditioning assumptions common to mirror descent methods. We back up our theory with experimental evidence on sampling from an ill-conditioned Gaussian distribution.

Acceleration and Implicit Regularization in Gaussian Phase Retrieval

We study accelerated optimization methods in the Gaussian phase retrieval problem. In this setting, we prove that gradient methods with Polyak or Nesterov momentum have similar implicit regularization to gradient descent. This implicit regularization ensures that the algorithms remain in a nice region, where the cost function is strongly convex and smooth despite being nonconvex in general. This ensures that these accelerated methods achieve faster rates of convergence than gradient descent. Experimental evidence demonstrates that the accelerated methods converge faster than gradient descent in practice.

Stochastic and Private Nonconvex Outlier-Robust PCA

We develop theoretically guaranteed stochastic methods for outlier-robust PCA. Outlier-robust PCA seeks an underlying low-dimensional linear subspace from a dataset that is corrupted with outliers. We are able to show that our methods, which involve stochastic geodesic gradient descent over the Grassmannian manifold, converge and recover an underlying subspace in various regimes through the development of a novel convergence analysis. The main application of this method is an effective differentially private algorithm for outlier-robust PCA that uses a Gaussian noise mechanism within the stochastic gradient method. Our results emphasize the advantages of the nonconvex methods over another convex approach to solving this problem in the differentially private setting. Experiments on synthetic and stylized data verify these results.

Scalable Cluster-Consistency Statistics for Robust Multi-Object Matching

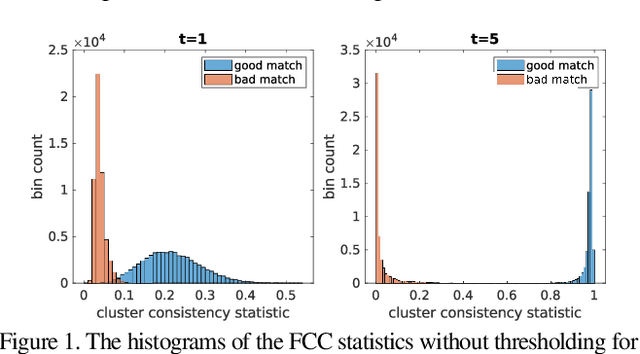
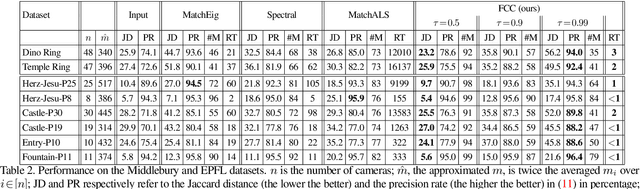
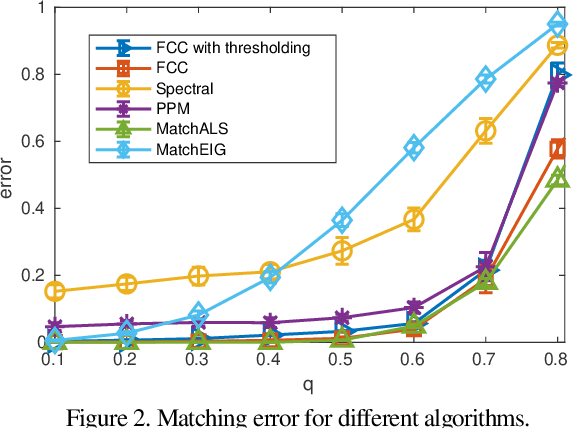
We develop new statistics for robustly filtering corrupted keypoint matches in the structure from motion pipeline. The statistics are based on consistency constraints that arise within the clustered structure of the graph of keypoint matches. The statistics are designed to give smaller values to corrupted matches and than uncorrupted matches. These new statistics are combined with an iterative reweighting scheme to filter keypoints, which can then be fed into any standard structure from motion pipeline. This filtering method can be efficiently implemented and scaled to massive datasets as it only requires sparse matrix multiplication. We demonstrate the efficacy of this method on synthetic and real structure from motion datasets and show that it achieves state-of-the-art accuracy and speed in these tasks.

Score-based Generative Neural Networks for Large-Scale Optimal Transport

We consider the fundamental problem of sampling the optimal transport coupling between given source and target distributions. In certain cases, the optimal transport plan takes the form of a one-to-one mapping from the source support to the target support, but learning or even approximating such a map is computationally challenging for large and high-dimensional datasets due to the high cost of linear programming routines and an intrinsic curse of dimensionality. We study instead the Sinkhorn problem, a regularized form of optimal transport whose solutions are couplings between the source and the target distribution. We introduce a novel framework for learning the Sinkhorn coupling between two distributions in the form of a score-based generative model. Conditioned on source data, our procedure iterates Langevin Dynamics to sample target data according to the regularized optimal coupling. Key to this approach is a neural network parametrization of the Sinkhorn problem, and we prove convergence of gradient descent with respect to network parameters in this formulation. We demonstrate its empirical success on a variety of large scale optimal transport tasks.

SVGD as a kernelized Wasserstein gradient flow of the chi-squared divergence

Stein Variational Gradient Descent (SVGD), a popular sampling algorithm, is often described as the kernelized gradient flow for the Kullback-Leibler divergence in the geometry of optimal transport. We introduce a new perspective on SVGD that instead views SVGD as the (kernelized) gradient flow of the chi-squared divergence which, we show, exhibits a strong form of uniform exponential ergodicity under conditions as weak as a Poincar\'e inequality. This perspective leads us to propose an alternative to SVGD, called Laplacian Adjusted Wasserstein Gradient Descent (LAWGD), that can be implemented from the spectral decomposition of the Laplacian operator associated with the target density. We show that LAWGD exhibits strong convergence guarantees and good practical performance.

Exponential ergodicity of mirror-Langevin diffusions

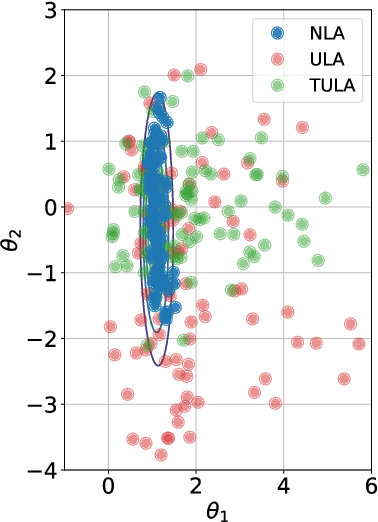
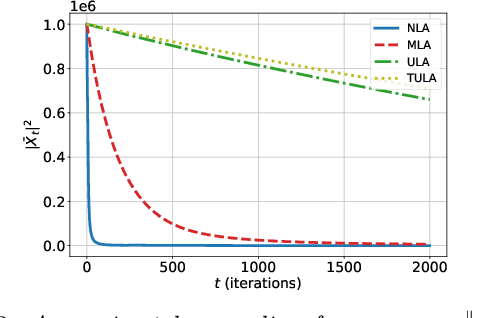
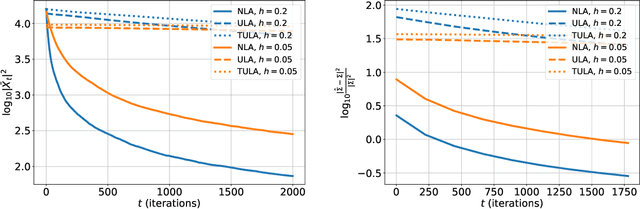
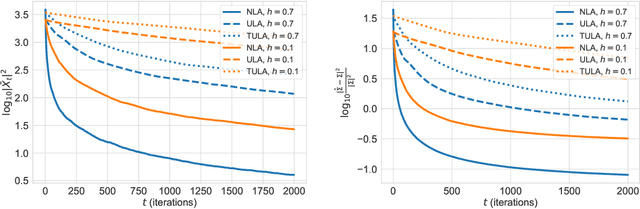
Motivated by the problem of sampling from ill-conditioned log-concave distributions, we give a clean non-asymptotic convergence analysis of mirror-Langevin diffusions as introduced in Zhang et al. (2020). As a special case of this framework, we propose a class of diffusions called Newton-Langevin diffusions and prove that they converge to stationarity exponentially fast with a rate which not only is dimension-free, but also has no dependence on the target distribution. We give an application of this result to the problem of sampling from the uniform distribution on a convex body using a strategy inspired by interior-point methods. Our general approach follows the recent trend of linking sampling and optimization and highlights the role of the chi-squared divergence. In particular, it yields new results on the convergence of the vanilla Langevin diffusion in Wasserstein distance.

A Provably Robust Multiple Rotation Averaging Scheme for SO(2)

We give adversarial robustness results for synchronization on the rotation group over $\mathbb{R}^2$, $\mathrm{SO}(2)$. In particular, we consider an adversarial corruption setting, where an adversary can choose which measurements to corrupt as well as what to corrupt them to. In this setting, we first show that some common nonconvex formulations, which are categorized as "multiple rotation averaging", may fail. We then discuss a new fast algorithm, called Trimmed Averaging Synchronization, which has exact recovery and linear convergence up to an outlier percentage of $1/4$.

Robust Subspace Recovery with Adversarial Outliers

We study the problem of robust subspace recovery (RSR) in the presence of adversarial outliers. That is, we seek a subspace that contains a large portion of a dataset when some fraction of the data points are arbitrarily corrupted. We first examine a theoretical estimator that is intractable to calculate and use it to derive information-theoretic bounds of exact recovery. We then propose two tractable estimators: a variant of RANSAC and a simple relaxation of the theoretical estimator. The two estimators are fast to compute and achieve state-of-the-art theoretical performance in a noiseless RSR setting with adversarial outliers. The former estimator achieves better theoretical guarantees in the noiseless case, while the latter estimator is robust to small noise, and its guarantees significantly improve with non-adversarial models of outliers. We give a complete comparison of guarantees for the adversarial RSR problem, as well as a short discussion on the estimation of affine subspaces.

A Well-Tempered Landscape for Non-convex Robust Subspace Recovery

We present a mathematical analysis of a non-convex energy landscape for robust subspace recovery. We prove that an underlying subspace is the only stationary point and local minimizer in a specified neighborhood under deterministic conditions on a dataset. If the deterministic condition is satisfied, we further show that a geodesic gradient descent method over the Grassmannian manifold can exactly recover the underlying subspace when the method is properly initialized. Proper initialization by principal component analysis is guaranteed with a similar deterministic condition. Under slightly stronger assumptions, the gradient descent method with a special shrinking step size scheme achieves linear convergence. The practicality of the deterministic condition is demonstrated on some statistical models of data, and the method achieves almost state-of-the-art recovery guarantees on the Haystack Model for different regimes of sample size and ambient dimension. In particular, when the ambient dimension is fixed and the sample size is large enough, we show that our gradient method can exactly recover the underlying subspace for any fixed fraction of outliers (less than 1).