Score-based Generative Neural Networks for Large-Scale Optimal Transport

We consider the fundamental problem of sampling the optimal transport coupling between given source and target distributions. In certain cases, the optimal transport plan takes the form of a one-to-one mapping from the source support to the target support, but learning or even approximating such a map is computationally challenging for large and high-dimensional datasets due to the high cost of linear programming routines and an intrinsic curse of dimensionality. We study instead the Sinkhorn problem, a regularized form of optimal transport whose solutions are couplings between the source and the target distribution. We introduce a novel framework for learning the Sinkhorn coupling between two distributions in the form of a score-based generative model. Conditioned on source data, our procedure iterates Langevin Dynamics to sample target data according to the regularized optimal coupling. Key to this approach is a neural network parametrization of the Sinkhorn problem, and we prove convergence of gradient descent with respect to network parameters in this formulation. We demonstrate its empirical success on a variety of large scale optimal transport tasks.

Generator Surgery for Compressed Sensing

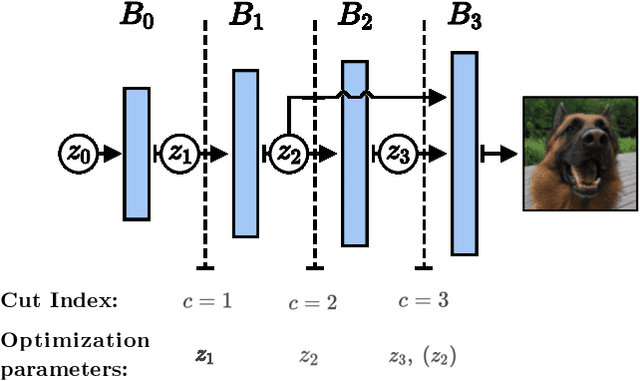
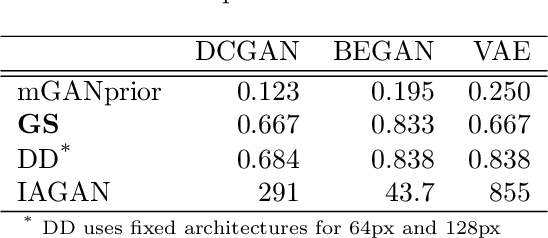
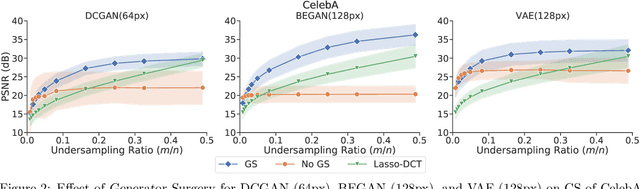
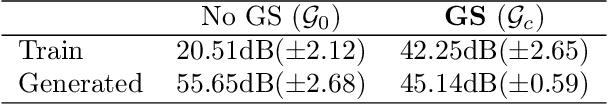
Image recovery from compressive measurements requires a signal prior for the images being reconstructed. Recent work has explored the use of deep generative models with low latent dimension as signal priors for such problems. However, their recovery performance is limited by high representation error. We introduce a method for achieving low representation error using generators as signal priors. Using a pre-trained generator, we remove one or more initial blocks at test time and optimize over the new, higher-dimensional latent space to recover a target image. Experiments demonstrate significantly improved reconstruction quality for a variety of network architectures. This approach also works well for out-of-training-distribution images and is competitive with other state-of-the-art methods. Our experiments show that test-time architectural modifications can greatly improve the recovery quality of generator signal priors for compressed sensing.

Reducing the Representation Error of GAN Image Priors Using the Deep Decoder

Generative models, such as GANs, learn an explicit low-dimensional representation of a particular class of images, and so they may be used as natural image priors for solving inverse problems such as image restoration and compressive sensing. GAN priors have demonstrated impressive performance on these tasks, but they can exhibit substantial representation error for both in-distribution and out-of-distribution images, because of the mismatch between the learned, approximate image distribution and the data generating distribution. In this paper, we demonstrate a method for reducing the representation error of GAN priors by modeling images as the linear combination of a GAN prior with a Deep Decoder. The deep decoder is an underparameterized and most importantly unlearned natural signal model similar to the Deep Image Prior. No knowledge of the specific inverse problem is needed in the training of the GAN underlying our method. For compressive sensing and image superresolution, our hybrid model exhibits consistently higher PSNRs than both the GAN priors and Deep Decoder separately, both on in-distribution and out-of-distribution images. This model provides a method for extensibly and cheaply leveraging both the benefits of learned and unlearned image recovery priors in inverse problems.