Equivariant Action Sampling for Reinforcement Learning and Planning

Reinforcement learning (RL) algorithms for continuous control tasks require accurate sampling-based action selection. Many tasks, such as robotic manipulation, contain inherent problem symmetries. However, correctly incorporating symmetry into sampling-based approaches remains a challenge. This work addresses the challenge of preserving symmetry in sampling-based planning and control, a key component for enhancing decision-making efficiency in RL. We introduce an action sampling approach that enforces the desired symmetry. We apply our proposed method to a coordinate regression problem and show that the symmetry aware sampling method drastically outperforms the naive sampling approach. We furthermore develop a general framework for sampling-based model-based planning with Model Predictive Path Integral (MPPI). We compare our MPPI approach with standard sampling methods on several continuous control tasks. Empirical demonstrations across multiple continuous control environments validate the effectiveness of our approach, showcasing the importance of symmetry preservation in sampling-based action selection.

Approximate Equivariance in Reinforcement Learning

Equivariant neural networks have shown great success in reinforcement learning, improving sample efficiency and generalization when there is symmetry in the task. However, in many problems, only approximate symmetry is present, which makes imposing exact symmetry inappropriate. Recently, approximately equivariant networks have been proposed for supervised classification and modeling physical systems. In this work, we develop approximately equivariant algorithms in reinforcement learning (RL). We define approximately equivariant MDPs and theoretically characterize the effect of approximate equivariance on the optimal Q function. We propose novel RL architectures using relaxed group convolutions and experiment on several continuous control domains and stock trading with real financial data. Our results demonstrate that approximate equivariance matches prior work when exact symmetries are present, and outperforms them when domains exhibit approximate symmetry. As an added byproduct of these techniques, we observe increased robustness to noise at test time.

Modeling Dynamics over Meshes with Gauge Equivariant Nonlinear Message Passing

Data over non-Euclidean manifolds, often discretized as surface meshes, naturally arise in computer graphics and biological and physical systems. In particular, solutions to partial differential equations (PDEs) over manifolds depend critically on the underlying geometry. While graph neural networks have been successfully applied to PDEs, they do not incorporate surface geometry and do not consider local gauge symmetries of the manifold. Alternatively, recent works on gauge equivariant convolutional and attentional architectures on meshes leverage the underlying geometry but underperform in modeling surface PDEs with complex nonlinear dynamics. To address these issues, we introduce a new gauge equivariant architecture using nonlinear message passing. Our novel architecture achieves higher performance than either convolutional or attentional networks on domains with highly complex and nonlinear dynamics. However, similar to the non-mesh case, design trade-offs favor convolutional, attentional, or message passing networks for different tasks; we investigate in which circumstances our message passing method provides the most benefit.

Can Euclidean Symmetry be Leveraged in Reinforcement Learning and Planning?

In robotic tasks, changes in reference frames typically do not influence the underlying physical properties of the system, which has been known as invariance of physical laws.These changes, which preserve distance, encompass isometric transformations such as translations, rotations, and reflections, collectively known as the Euclidean group. In this work, we delve into the design of improved learning algorithms for reinforcement learning and planning tasks that possess Euclidean group symmetry. We put forth a theory on that unify prior work on discrete and continuous symmetry in reinforcement learning, planning, and optimal control. Algorithm side, we further extend the 2D path planning with value-based planning to continuous MDPs and propose a pipeline for constructing equivariant sampling-based planning algorithms. Our work is substantiated with empirical evidence and illustrated through examples that explain the benefits of equivariance to Euclidean symmetry in tackling natural control problems.

A General Theory of Correct, Incorrect, and Extrinsic Equivariance

Although equivariant machine learning has proven effective at many tasks, success depends heavily on the assumption that the ground truth function is symmetric over the entire domain matching the symmetry in an equivariant neural network. A missing piece in the equivariant learning literature is the analysis of equivariant networks when symmetry exists only partially in the domain. In this work, we present a general theory for such a situation. We propose pointwise definitions of correct, incorrect, and extrinsic equivariance, which allow us to quantify continuously the degree of each type of equivariance a function displays. We then study the impact of various degrees of incorrect or extrinsic symmetry on model error. We prove error lower bounds for invariant or equivariant networks in classification or regression settings with partially incorrect symmetry. We also analyze the potentially harmful effects of extrinsic equivariance. Experiments validate these results in three different environments.

The Surprising Effectiveness of Equivariant Models in Domains with Latent Symmetry

Extensive work has demonstrated that equivariant neural networks can significantly improve sample efficiency and generalization by enforcing an inductive bias in the network architecture. These applications typically assume that the domain symmetry is fully described by explicit transformations of the model inputs and outputs. However, many real-life applications contain only latent or partial symmetries which cannot be easily described by simple transformations of the input. In these cases, it is necessary to learn symmetry in the environment instead of imposing it mathematically on the network architecture. We discover, surprisingly, that imposing equivariance constraints that do not exactly match the domain symmetry is very helpful in learning the true symmetry in the environment. We differentiate between extrinsic and incorrect symmetry constraints and show that while imposing incorrect symmetry can impede the model's performance, imposing extrinsic symmetry can actually improve performance. We demonstrate that an equivariant model can significantly outperform non-equivariant methods on domains with latent symmetries both in supervised learning and in reinforcement learning for robotic manipulation and control problems.

Robust Imitation of a Few Demonstrations with a Backwards Model

Behavior cloning of expert demonstrations can speed up learning optimal policies in a more sample-efficient way over reinforcement learning. However, the policy cannot extrapolate well to unseen states outside of the demonstration data, creating covariate shift (agent drifting away from demonstrations) and compounding errors. In this work, we tackle this issue by extending the region of attraction around the demonstrations so that the agent can learn how to get back onto the demonstrated trajectories if it veers off-course. We train a generative backwards dynamics model and generate short imagined trajectories from states in the demonstrations. By imitating both demonstrations and these model rollouts, the agent learns the demonstrated paths and how to get back onto these paths. With optimal or near-optimal demonstrations, the learned policy will be both optimal and robust to deviations, with a wider region of attraction. On continuous control domains, we evaluate the robustness when starting from different initial states unseen in the demonstration data. While both our method and other imitation learning baselines can successfully solve the tasks for initial states in the training distribution, our method exhibits considerably more robustness to different initial states.

Learning Symmetric Embeddings for Equivariant World Models

Incorporating symmetries can lead to highly data-efficient and generalizable models by defining equivalence classes of data samples related by transformations. However, characterizing how transformations act on input data is often difficult, limiting the applicability of equivariant models. We propose learning symmetric embedding networks (SENs) that encode an input space (e.g. images), where we do not know the effect of transformations (e.g. rotations), to a feature space that transforms in a known manner under these operations. This network can be trained end-to-end with an equivariant task network to learn an explicitly symmetric representation. We validate this approach in the context of equivariant transition models with 3 distinct forms of symmetry. Our experiments demonstrate that SENs facilitate the application of equivariant networks to data with complex symmetry representations. Moreover, doing so can yield improvements in accuracy and generalization relative to both fully-equivariant and non-equivariant baselines.

Generator Surgery for Compressed Sensing

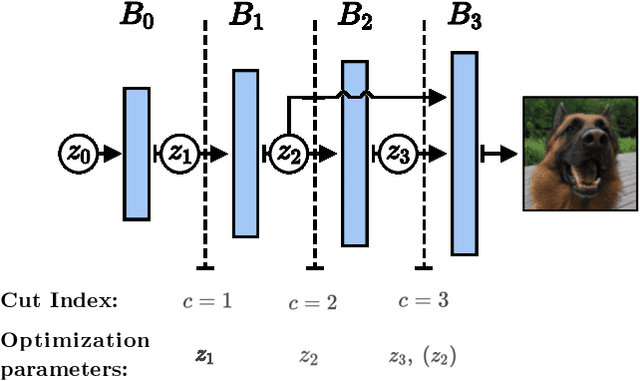
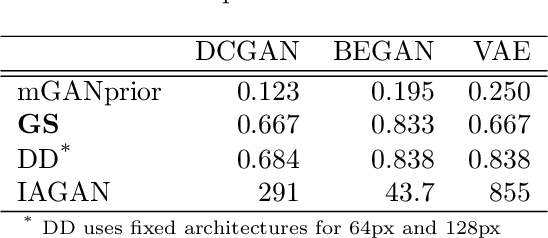
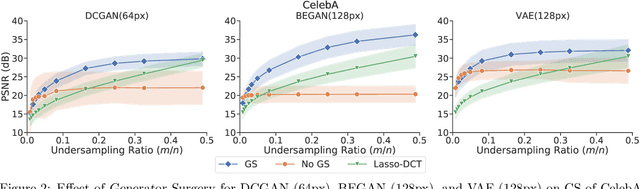
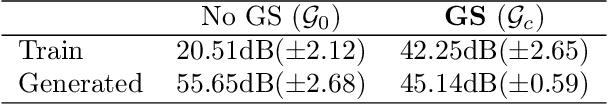
Image recovery from compressive measurements requires a signal prior for the images being reconstructed. Recent work has explored the use of deep generative models with low latent dimension as signal priors for such problems. However, their recovery performance is limited by high representation error. We introduce a method for achieving low representation error using generators as signal priors. Using a pre-trained generator, we remove one or more initial blocks at test time and optimize over the new, higher-dimensional latent space to recover a target image. Experiments demonstrate significantly improved reconstruction quality for a variety of network architectures. This approach also works well for out-of-training-distribution images and is competitive with other state-of-the-art methods. Our experiments show that test-time architectural modifications can greatly improve the recovery quality of generator signal priors for compressed sensing.

Multiresolution Tensor Learning for Efficient and Interpretable Spatial Analysis

Efficient and interpretable spatial analysis is crucial in many fields such as geology, sports, and climate science. Large-scale spatial data often contains complex higher-order correlations across features and locations. While tensor latent factor models can describe higher-order correlations, they are inherently computationally expensive to train. Furthermore, for spatial analysis, these models should not only be predictive but also be spatially coherent. However, latent factor models are sensitive to initialization and can yield inexplicable results. We develop a novel Multi-resolution Tensor Learning (MRTL) algorithm for efficiently learning interpretable spatial patterns. MRTL initializes the latent factors from an approximate full-rank tensor model for improved interpretability and progressively learns from a coarse resolution to the fine resolution for an enormous computation speedup. We also prove the theoretical convergence and computational complexity of MRTL. When applied to two real-world datasets, MRTL demonstrates 4 ~ 5 times speedup compared to a fixed resolution while yielding accurate and interpretable models.