NeuralPLexer3: Accurate Biomolecular Complex Structure Prediction with Flow Models

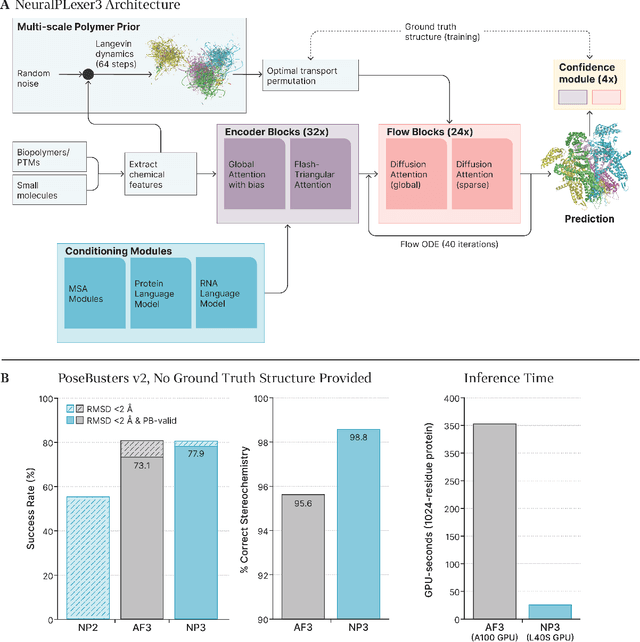
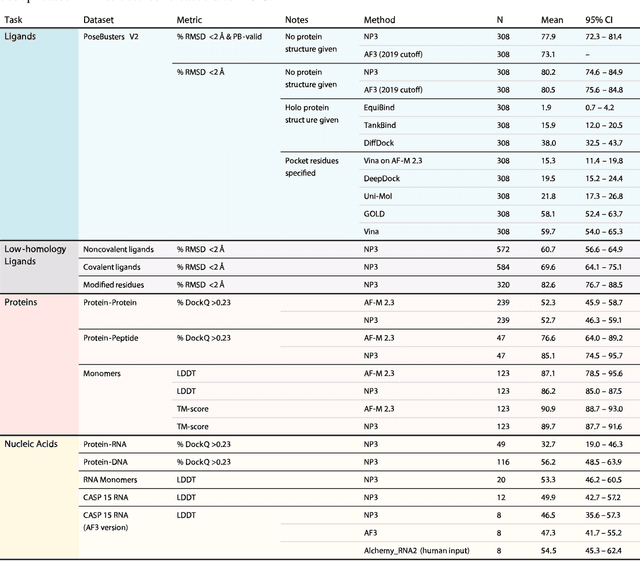
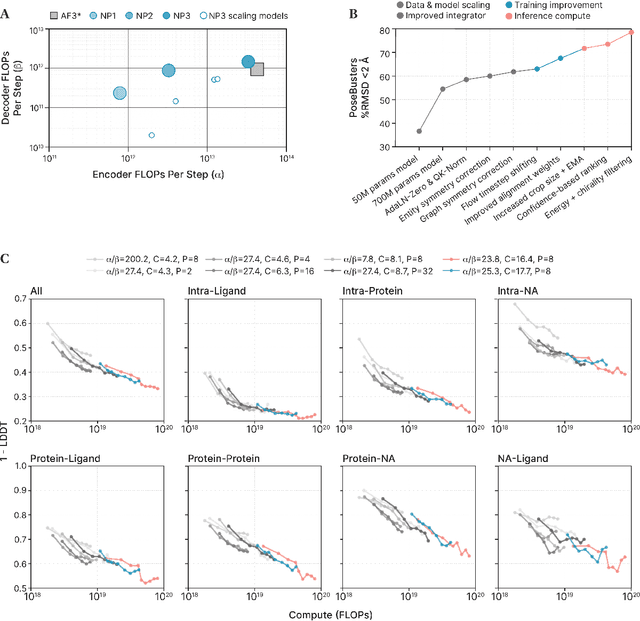
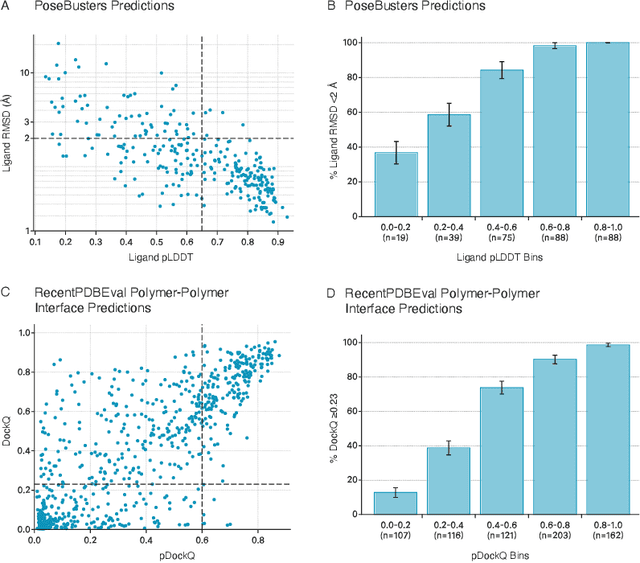
Structure determination is essential to a mechanistic understanding of diseases and the development of novel therapeutics. Machine-learning-based structure prediction methods have made significant advancements by computationally predicting protein and bioassembly structures from sequences and molecular topology alone. Despite substantial progress in the field, challenges remain to deliver structure prediction models to real-world drug discovery. Here, we present NeuralPLexer3 -- a physics-inspired flow-based generative model that achieves state-of-the-art prediction accuracy on key biomolecular interaction types and improves training and sampling efficiency compared to its predecessors and alternative methodologies. Examined through newly developed benchmarking strategies, NeuralPLexer3 excels in vital areas that are crucial to structure-based drug design, such as physical validity and ligand-induced conformational changes.

Equivariant Action Sampling for Reinforcement Learning and Planning

Reinforcement learning (RL) algorithms for continuous control tasks require accurate sampling-based action selection. Many tasks, such as robotic manipulation, contain inherent problem symmetries. However, correctly incorporating symmetry into sampling-based approaches remains a challenge. This work addresses the challenge of preserving symmetry in sampling-based planning and control, a key component for enhancing decision-making efficiency in RL. We introduce an action sampling approach that enforces the desired symmetry. We apply our proposed method to a coordinate regression problem and show that the symmetry aware sampling method drastically outperforms the naive sampling approach. We furthermore develop a general framework for sampling-based model-based planning with Model Predictive Path Integral (MPPI). We compare our MPPI approach with standard sampling methods on several continuous control tasks. Empirical demonstrations across multiple continuous control environments validate the effectiveness of our approach, showcasing the importance of symmetry preservation in sampling-based action selection.

Equivariant Offline Reinforcement Learning

Sample efficiency is critical when applying learning-based methods to robotic manipulation due to the high cost of collecting expert demonstrations and the challenges of on-robot policy learning through online Reinforcement Learning (RL). Offline RL addresses this issue by enabling policy learning from an offline dataset collected using any behavioral policy, regardless of its quality. However, recent advancements in offline RL have predominantly focused on learning from large datasets. Given that many robotic manipulation tasks can be formulated as rotation-symmetric problems, we investigate the use of $SO(2)$-equivariant neural networks for offline RL with a limited number of demonstrations. Our experimental results show that equivariant versions of Conservative Q-Learning (CQL) and Implicit Q-Learning (IQL) outperform their non-equivariant counterparts. We provide empirical evidence demonstrating how equivariance improves offline learning algorithms in the low-data regime.

Fourier Transporter: Bi-Equivariant Robotic Manipulation in 3D

Many complex robotic manipulation tasks can be decomposed as a sequence of pick and place actions. Training a robotic agent to learn this sequence over many different starting conditions typically requires many iterations or demonstrations, especially in 3D environments. In this work, we propose Fourier Transporter (\ours{}) which leverages the two-fold $\SE(d)\times\SE(d)$ symmetry in the pick-place problem to achieve much higher sample efficiency. \ours{} is an open-loop behavior cloning method trained using expert demonstrations to predict pick-place actions on new environments. \ours{} is constrained to incorporate symmetries of the pick and place actions independently. Our method utilizes a fiber space Fourier transformation that allows for memory-efficient construction. We test our proposed network on the RLbench benchmark and achieve state-of-the-art results across various tasks.

Multi-Irreducible Spectral Synchronization for Robust Rotation Averaging

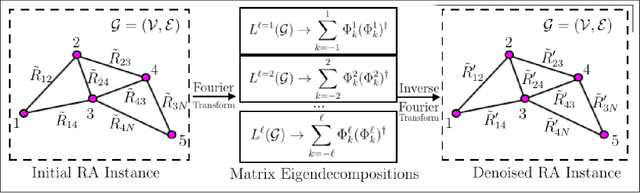
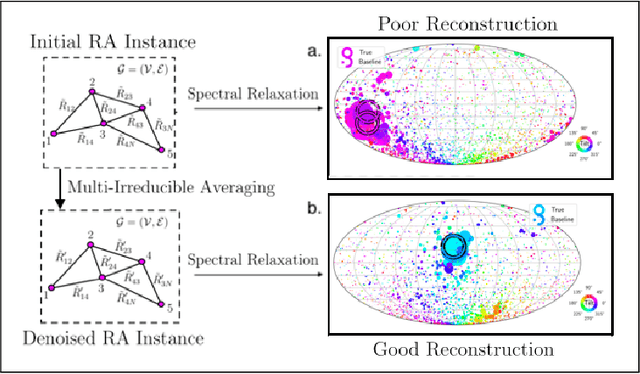
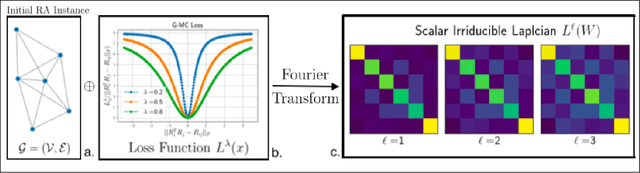
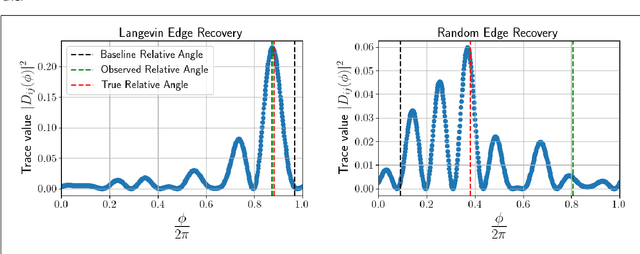
Rotation averaging (RA) is a fundamental problem in robotics and computer vision. In RA, the goal is to estimate a set of $N$ unknown orientations $R_{1}, ..., R_{N} \in SO(3)$, given noisy measurements $R_{ij} \sim R^{-1}_{i} R_{j}$ of a subset of their pairwise relative rotations. This problem is both nonconvex and NP-hard, and thus difficult to solve in the general case. We apply harmonic analysis on compact groups to derive a (convex) spectral relaxation constructed from truncated Fourier decompositions of the individual summands appearing in the RA objective; we then recover an estimate of the RA solution by computing a few extremal eigenpairs of this relaxation, and (approximately) solving a consensus problem. Our approach affords several notable advantages versus prior RA methods: it can be used in conjunction with \emph{any} smooth loss function (including, but not limited to, robust M-estimators), does not require any initialization, and is implemented using only simple (and highly scalable) linear-algebraic computations and parallelizable optimizations over band-limited functions of individual rotational states. Moreover, under the (physically well-motivated) assumption of multiplicative Langevin measurement noise, we derive explicit performance guarantees for our spectral estimator (in the form of probabilistic tail bounds on the estimation error) that are parameterized in terms of graph-theoretic quantities of the underlying measurement network. By concretely linking estimator performance with properties of the underlying measurement graph, our results also indicate how to devise measurement networks that are \emph{guaranteed} to achieve accurate estimation, enabling such downstream tasks as sensor placement, network compression, and active sensing.

Can Euclidean Symmetry be Leveraged in Reinforcement Learning and Planning?

In robotic tasks, changes in reference frames typically do not influence the underlying physical properties of the system, which has been known as invariance of physical laws.These changes, which preserve distance, encompass isometric transformations such as translations, rotations, and reflections, collectively known as the Euclidean group. In this work, we delve into the design of improved learning algorithms for reinforcement learning and planning tasks that possess Euclidean group symmetry. We put forth a theory on that unify prior work on discrete and continuous symmetry in reinforcement learning, planning, and optimal control. Algorithm side, we further extend the 2D path planning with value-based planning to continuous MDPs and propose a pipeline for constructing equivariant sampling-based planning algorithms. Our work is substantiated with empirical evidence and illustrated through examples that explain the benefits of equivariance to Euclidean symmetry in tackling natural control problems.

Equivariant Single View Pose Prediction Via Induced and Restricted Representations

Learning about the three-dimensional world from two-dimensional images is a fundamental problem in computer vision. An ideal neural network architecture for such tasks would leverage the fact that objects can be rotated and translated in three dimensions to make predictions about novel images. However, imposing SO(3)-equivariance on two-dimensional inputs is difficult because the group of three-dimensional rotations does not have a natural action on the two-dimensional plane. Specifically, it is possible that an element of SO(3) will rotate an image out of plane. We show that an algorithm that learns a three-dimensional representation of the world from two dimensional images must satisfy certain geometric consistency properties which we formulate as SO(2)-equivariance constraints. We use the induced and restricted representations of SO(2) on SO(3) to construct and classify architectures which satisfy these geometric consistency constraints. We prove that any architecture which respects said consistency constraints can be realized as an instance of our construction. We show that three previously proposed neural architectures for 3D pose prediction are special cases of our construction. We propose a new algorithm that is a learnable generalization of previously considered methods. We test our architecture on three pose predictions task and achieve SOTA results on both the PASCAL3D+ and SYMSOL pose estimation tasks.

Machine Learning as Ecology

Machine learning methods have had spectacular success on numerous problems. Here we show that a prominent class of learning algorithms - including Support Vector Machines (SVMs) -- have a natural interpretation in terms of ecological dynamics. We use these ideas to design new online SVM algorithms that exploit ecological invasions, and benchmark performance using the MNIST dataset. Our work provides a new ecological lens through which we can view statistical learning and opens the possibility of designing ecosystems for machine learning. Supplemental code is found at https://github.com/owenhowell20/EcoSVM.